Kompressiokonsepti ja kaavat, laskelmat, esimerkit, harjoitukset

Se pakkaus- tai puristuspyrkimykset Se on pinta -alayksikköä kohti, jonka tuloksena on työntää, kiristää tai puristaa esine, pyrkii lyhentämään sitä. Matemaattisesti on:

E = f /a

Tässä JA Merkitä ponnisteluja, F voiman suuruus ja -Lla Alue, jolla yksikkö on kansainvälisessä järjestelmässä, jos Newton/M² o Pascal (PA). Puristuspyrkimykset ovat a normaali ponnistus, Koska sen tuottava voima on kohtisuorassa alueelle, jolla se on.

Kuvio 1. Ateenan akropolin sarakkeet ovat puristuneet. Lähde: Pixabay.

Tällainen pyrkimys voi puristaa esineen tai päinvastoin, kiristää ja venyttää sitä, kuten levitetään. Kompressiopyrkimyksen tapauksessa voimat sovelletaan vastakkaiseen suuntaan esineen kiristämisen ja lyhentämisen vaikutuksen aikaansaamiseksi.

Kun joukot lakkaavat, monet materiaalit palaavat alkuperäisiin mitoihinsa. Tämä ominaisuus tunnetaan nimellä joustavuus. Mutta vaikka niin tapahtuu, yhtenäisen joustava muodonmuutos, jonka materiaali on vaivaa, on:

Yhtenäinen muodonmuutos = (lopullinen koko - alkukoko)/alkukoko

Muodonmuutos voi olla lineaarinen, pinnallinen tai tilavuus, vaikka yksikön muodonmuutoksista puuttuu yksiköitä. Sen tarjoamat tiedot ovat kuitenkin erittäin tärkeitä, koska ei ole sama muodonmuutos 10 m pitkä baari 1 cm: ssä, muodonmuutos 1cm vielä 1 m pitkä palkki.

Joustavassa materiaalissa muodonmuutos ja vaivat ovat verrannollisia, noudattaen Hooken lakia:

Ponnistus ∝ yhtenäisen muodonmuutoksen

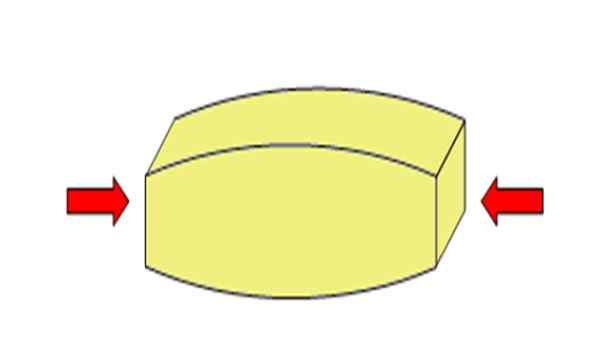Kuva 2. Kompressiopyrkimys vähentää esineen pituutta. Lähde: Wikimedia Commons. Adre-es [CC BY-SA 4.0 (https: // creativecommons.Org/lisenssit/by-SA/4.0)].[TOC]

¿Kuinka laskea puristus?

Kompressiopyrkimys saa materiaalin hiukkaset lähemmäksi ja lisäämään niiden kokoa. Pyrkimyksen kohdasta riippuen, mikä tahansa sen mitat lyhenevät tai vähenevät.

Voi palvella sinua: Atomin kvantmekaaninen malli

Aloitetaan olettamalla ohuen alkuperäisen pituuden palkki Lens,  mihin normaalia suuruusponnistusta käytetään JA. Jos ponnistus on pakkausta, palkki kokee sen pituuden vähenemisen, jonka merkitsee Δ. Jos se on jännitystä, palkkia pidennetään.

Luonnollisesti materiaali, jonka elementti tehdään, on ratkaiseva kyvyssään tukea ponnisteluja.

Nämä materiaalin joustavat ominaisuudet sisältyvät edellä mainittuun suhteellisuusvakioon. Kutsutaan joustavuusmoduuli jompikumpi Nuori moduuli Ja se on merkitty nimellä ja. Jokaisella materiaalilla on joustavuusmoduuli, joka määritetään kokeellisesti laboratoriokokeilla.

Tätä silmällä pitäen vaivaa JA Se ilmaistaan ​​matemaattisella tavalla näin:

Ponnistus ∝ yhtenäisen muodonmuutoksen

Lopuksi tämän ehdon määrittämiseksi yhtälöksi vaaditaan suhteellisuusvakion suhteellisuuden korvaamiseksi ja korvaa se tasa -arvolla, kuten tämä:

Ponnistus = suhteellisuusvakio x yksikön muodonmuutos        

E = y. (Δ /L)

Osamäärä (Δ /L) Se on yhtenäinen muodonmuutos, merkitty nimellä ε ja Δ = Lopullinen pituus - alkuperäinen pituus. Tällä tavalla ponnistus JA Se pysyy seuraavasti:

E = y. ε

Koska yksikön muodonmuutos on ulottumaton, yksiköt JA ovat samat kuin JA: N/m² tai PA SI -järjestelmässä, puntia/sisään² o psi brittiläisessä järjestelmässä, samoin kuin muut vahvuus- ja alueyhdistelmät, kuten kg/cm².

Eri materiaalien joustavuusmoduuli

Arvot ja määritetään kokeellisesti laboratoriossa, kontrolloiduissa olosuhteissa. Seuraavaksi joustavuusmoduuli materiaaleille, joita käytetään laajasti rakentamisessa ja myös luiden, moduulissa:

Voi palvella sinua: Vektorit avaruudessa: Kuinka kuvaaja, sovellukset, harjoitukset

pöytä 1

Materiaali	Joustavuusmoduuli y (pa) x 109
Teräs	200
Rauta	100
Messinki	100
Pronssi	90
Alumiini	70
Marmori	viisikymmentä
Graniitti	Neljä viisi
Betoni	kaksikymmentä
Luu	viisitoista
Mänty	10

Esimerkit

Kompressiopyrkimykset toimivat erilaisiin rakenteisiin; Sama, johon sovelletaan voimia, kuten kunkin niiden muodostavien elementtien paino, samoin kuin ulkoisten aineiden voimat: tuuli, lumi, muut rakenteet ja muut.

On tavallista, että useimmat rakenteet suunnitellaan vastustamaan kaikenlaisia ​​ponnisteluja ilman muodonmuutoksia. Siksi on tarpeen ottaa huomioon puristuspyrkimy.

Myös luurankon luut ovat rakenteita, jotka ovat alaisia ​​erilaisilla ponnisteluilla. Vaikka luut ovat vastustuskykyisiä heille, kun elastinen raja ylitetään vahingossa, halkeamat ja murtumat ovat peräisin.

Pylväät ja pylväät

Rakennusten pylväät ja pylväät on tehtävä vastustamaan puristusta, muuten niillä on taipumus arkeilla. Tämä tunnetaan nimellä sivuttainen taivutus jompikumpi taipuminen.

Sarakkeet (katso kuva 1) ovat elementtejä, joiden pituus on paljon korkeampi verrattuna sen poikkileikkauksen pinta -alaan.

Sylinterimäinen elementti on pylväs, kun sen pituus on yhtä suuri kuin yli kymmenen kertaa poikkileikkauksen halkaisija. Mutta jos poikkileikkaus ei ole vakio, sen pienempi halkaisija otetaan elementin luokittelemiseksi sarakkeeksi.

Tuolit ja pankit

Kun ihmiset istuvat huonekaluissa, kuten tuolit ja pankit tai lisäävät esineitä päälle, jalat ovat puristuspyrkimyksiä, joilla on taipumus vähentää heidän korkeuttaan.

Kuva 3. Istuessaan ihmiset tekevät puristusponnistelua tuolille, jolla on taipumus lyhentää heidän korkeuttaan. Lähde: Pixabay.

Yleensä huonekalut saadaan vastustamaan painoa melko hyvin ja palaamaan heidän luonnolliseen tilaansa, kun se on poistettu. Mutta jos hauraisiin tuoleihin tai pankkeihin sijoitetaan suuri paino, jalat tuottavat puristusta ja rikkoutumista.

Voi palvella sinua: sähköjohtimet

Harjoitukset

- Harjoitus 1

Sinulla on sauva, jonka pituus on alun perin 12 metriä, joihin se käy läpi puristusponnistuksen siten, että sen yksikön muodonmuutos on -0.0004. Mikä on uusi sauvan pituus?

Ratkaisu

Alkaen yllä annetusta yhtälöstä:

ε = (Δ /L) = - 0.0004

Joo Lens_F Se on lopullinen pituus ja Lens_jompikumpi Alkuperäinen pituus siitä lähtien Δ = l_F - Lens_jompikumpi  Sinulla on:

(L_F - Lens_jompikumpi)/ L_jompikumpi = -0.0004

Siksi: Lens_F - Lens_jompikumpi = -0.0004 x 12 m = -0.0048 m. Ja lopuksi:

Lens_F  = (12 - 0.0048) M = 11.9952 m.

- Harjoitus 2

Kiinteä terästanko, lieriömäinen, on halkaisijaltaan 6 m pitkä ja 8 cm. Jos palkki puristuu 90 kuorman avulla.000 kg, löydä:

a) Megapascal (MPA): n puristusponnistelujen suuruus

b) kuinka paljon palkin pituus laski?

Liittää jhk

Ensimmäinen on palkin poikkileikkauksen alue, joka riippuu sen halkaisijasta D, mikä johtaa:

A = π. D -d² / 4 = π. (0.08 m)² / 4 = 5.03 x 10^-3 m²

Voima on heti läpi F = m.G = 90.000 kg x 9.8 m/s²= 882.000 n.

Lopuksi keskimääräinen ponnistus lasketaan seuraavasti:

E = f/ a = 882.000 N/ 5.03 x 10^-3 m² = 1.75 x 10⁸ PA = 175 MPa

Ratkaisu b

Pyrkimyksen yhtälöä käytetään nyt tietäen, että materiaalilla on joustava vaste:

E = y. (Δ /L)

Teräs nuori moduuli löytyy taulukosta 1:

Δ = e.L / y = 6 m x 1.75 x 10⁸ PA / 200 x 10 ⁹ PA = 5.25 x 10 ^-3 M = 5.25 mm.

Viitteet

1. Olut, f. 2010. Materiaalimekaniikka. Viides. Painos. McGraw Hill.
2. Giancoli, D.  2006. Fysiikka: sovellusten periaatteet. 6^Tth  Ed. Prentice Hall.
3. Hibbeler, R.C. 2006. Materiaalimekaniikka. Kuudes. Painos. Pearson -koulutus.
4. Tippens, P. 2011. Fysiikka: Käsitteet ja sovellukset. 7. painos. McGraw Hill
5. Wikipedia. Stressi (mekaniikka). Toipunut: Wikipedia.org.