Tasapainotusolosuhteiden käsite, sovellukset ja esimerkit

Se tasapainoolosuhteet Ne ovat välttämättömiä, jotta vartalo pysyy levossa tai tasaisen suorakulmion liikkeessä. Ensimmäisessä tapauksessa sanotaan, että objekti on staattisessa tasapainossa, kun taas toisessa se on dynaamisessa tasapainossa.

Olettaen, että liikkuva esine on hiukkas, jolloin mittoja ei oteta huomioon, riittää, että siihen vaikuttavien voimien summa on muokattu.

Kuvio 1. Brimhamin kivet Pohjois -Englannissa täyttävät tasapainoolosuhteet. Lähde: Julkiset alueet.netto.

Mutta suurella enemmistöllä liikkuvista esineistä on tuntuvia ulottuvuuksia, joten tämä ehto ei riitä tasapainon takaamiseen, mikä joka tapauksessa on kiihtyvyyden puuttuminen, ei liikkeestä.

[TOC]

Ensimmäinen ja toinen tasapainotila

Katsotaanpa: Jos voimien summa on tyhjä, on totta, että esine ei aio liikkua tai liikkua nopeasti, mutta se voi silti alkaa kääntyä.

Siksi kiertojen välttämiseksi toisen tilan on.

Lyhyesti sanottuna, merkitseminen miten F Nettovoima ja τ jompikumpi M Nettomomentin vektoriin meillä on:

Ensimmäinen tasapainon kunto

∑ F = 0 -

Mikä tarkoittaa, että: ∑ f_x = 0, ∑ f_ja = 0 ja ∑ f_{z -z} = 0

Toinen tasapainotila

∑ τ = 0 - tai ∑ M = 0 -

Minkä tahansa pisteen suhteen laskettujen vääntömomenttien tai hetkien kanssa.

Seuraavassa oletamme, että mobiili objekti on jäykkä runko, joka ei koe muodonmuutoksia.

Sovellukset

Vaikka liike näyttää olevan yleinen nimittäjä maailmankaikkeudessa, tasapaino on myös monissa luonnon näkökohdissa ja meitä ympäröivissä esineissä.

Voi palvella sinua: Millikan -kokeilu: Menettely, selitys, merkitys

Isostaattinen tasapaino

Planeetta -asteikolla maa on isostaattinen tasapaino, Eräänlainen maapallon kuoren painovoima, jonka tiheys ei ole yhtenäinen.

Maankuoren eri lohkojen tai alueiden tiheyksien erot kompensoidaan planeetan orografialle ominaisia ​​korkeuseroja. Se toimii samalla tavalla, että eri materiaalit upottavat enemmän tai vähemmän vedessä niiden tiheyden mukaan ja saavuttavat tasapainon.

Mutta koska kuoren lohkot eivät kellu vedessä, vaan vaippassa, mikä on paljon viskoosista, tasapainoa ei kutsu.

Fuusiotoiminta ytimessä

Tähteissä kuin aurinko, tasapaino, joka pakattu painovoiman ja niitä laajentavan hydrostaattisen paineen välillä, pitää fuusioreaktorin toiminnassa tähden ytimessä, joka pitää sen hengissä. Olemme riippuvaisia ​​tästä tasapainosta niin, että maa saa tarvittavan valon ja lämmön.

Rakennus

Paikallisessa mittakaavassa haluamme,.

Siksi syntyi staattinen, joka on mekaniikan haara, joka on omistettu tutkimaan kehon tasapainoa ja kaikkea mitä tarvitaan niiden pitämiseen näin.

Staattiset tasapainotyypit

Käytännössä havaitsemme, että staattinen saldo voi olla kolmesta luokasta:

Tasapaino

Se tapahtuu, kun esine liikkuu asennosta ja palaa heti siihen, kun sitä siirsivät voima. Mitä lähempänä maaperän kohdetta, sitä todennäköisemmin on välttämätöntä olla vakaassa tasapainossa.

Voi palvella sinua: näennäinen tiheys: kaava, yksiköt ja harjoitukset ratkaistu

Oikeanpuoleinen pallo kuvassa 2 on hyvä esimerkki, jos otamme sen pois sen tasapainosasennosta kulhon alaosassa, painovoima vastaa nopeasti palaamisesta.

Välinpitämätön tai neutraali saldo

Se tapahtuu, kun esine siirretään huolimatta. Pyöreät esineet, kuten pallo, kun ne asetetaan tasaisille pinnoille, ovat välinpitämättömiä tasapainoja.

Epävakaa tasapaino

Se tapahtuu, kun objekti siirtyy tasapainopaikastaan, se ei palaa siihen. Jos pidämme palloa vasemmalla olevan mäen rinnalla, on varmaa, että se ei palaa omilla keinoillaan.

Kuva 2. Saldotyypit. Lähde: Wikimedia Commons.

Esimerkki: hiukkasten staattinen

Oletetaan, että massa m Kaltevalla tasolla, jonka on tarkoitus keskittyä sen geometriseen keskukseen.

Painon w vaakakomponentti_x Sillä on taipumus saada lohko liukua, joten toinen voima, joka vastustaa. Jos haluamme, että lohko pysyy levossa, tämä voima on staattinen kitka. Mutta jos annamme lohkon liukastua alamäkeen vakiona nopeudella, tarvittava lujuus on dynaaminen kitka.

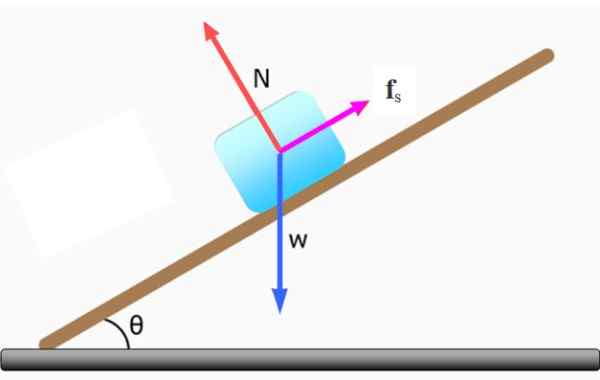Kuva 3. Lohko pysyy staattisessa saldossa kaltevalla tasolla. Lähde: f. Zapata.

Kitkan puuttuessa lohko liukuu alakertaan, ja siinä tapauksessa ei ole tasapainoa.

Jotta lohko olisi levossa, siihen vaikuttavat voimat: paino W -, Normaali N ja staattinen kitka F_s, Ne on korvattava. Niin:

∑ f_ja = 0 → N - W_ja = 0

∑ f_x = 0 → W_x - F_s = 0

Staattinen kitka tasapainottaa painon vaakasuoran komponentin: W_x = f_s ja siksi:

F_s = m . g .synti θ

Liikuntaa

Liikennevalo 21.5 kg roikkuu homogeenisesta AB -alumiinipalkista 12 kg massaa ja 7.5 m pitkä, CD -vaakasuoran köyden ylläpitämä, kuten kuvassa esitetään. Löytö:

Voi palvella sinua: Päätelulause: Selitys, sovellukset, ratkaisut harjoitukset

a) CD -kaapelijännite

b) Postin kääntövoiman vaaka- ja pystysuuntaiset komponentit.

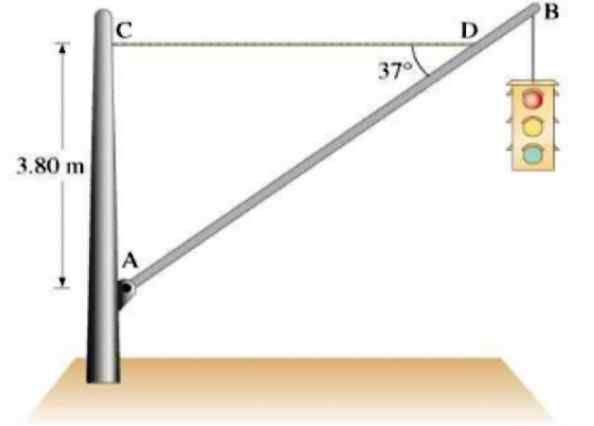Kuva 4.- Liikennevalo roikkuu alumiinipalkista staattisessa tasapainossa. Lähde: Giancoli. D -d. Fysiikka sovelluksilla.

Ratkaisu

Baariin kohdistuva voimakaavio on rakennettu painon kanssa W -, Kääntöreaktion jousissa ja vaakasuorat ja pystysuuntaiset komponentit, nimeltään r_x ja r_ja. Sitten tasapainoolosuhteet koskevat.

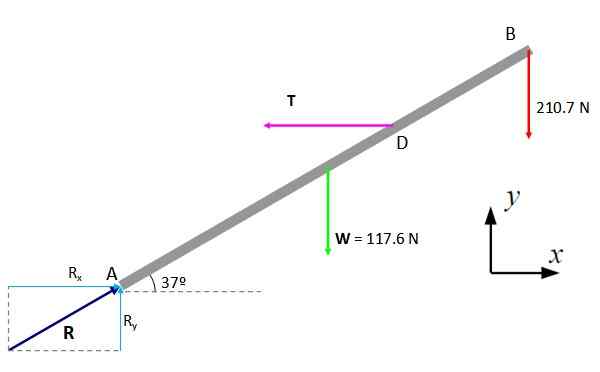Kuva 5. Vapaa kehon kaavio palkkiin. Lähde: f. Zapata.

Ensimmäinen kunto

Ensimmäinen tasapainotila on ongelma lentokoneessa, se tarjoaa kaksi yhtälöä:

Σf_x = 0
Σf_ja = 0

Ensimmäisestä:

R -_x - T = 0

R -_x = T

Ja toinen:

R -_ja - 117.6 n - 210.7 n = 0

R -_ja = 328.3 n

Reaktion vaakasuora komponentti on yhtä suuruus kuin T -jännite.

Toinen kunto

Kuvion 5 kohta A valitaan käännöskeskukseksi, tällä tavalla reaktiovarsi R - Se on tyhjä, muista, että hetken suuruus on annettu:

M = f_┴ d -d

Missä f_┴ Se on voiman kohtisuora komponentti ja D on kierto -akselin ja voiman levityspisteen välinen etäisyys. Saamme yhtälön:

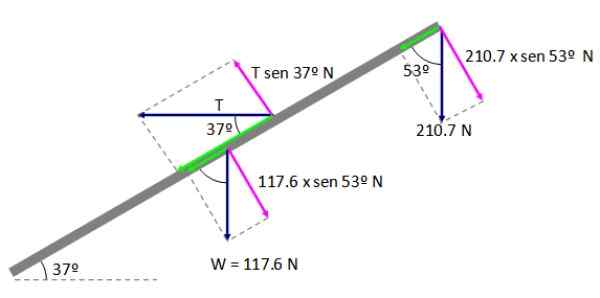Kuva 6. Hetkiä kohtaan a. Lähde: f. Zapata.

Σm_-Lla = 0

(210.7 × Sen 53º) AB + (117.6 × SEN 53º) (AB/2) - (T × Sen 37º) AD = 0

Etäisyysmainos on:

AD = (3.8 m / sin 37º) = 6.3 m

(210.7 × Sen 53º N) (7.5 m) + (117.6 × Sen 53º N) (3.75 m) - (T × Sen 37º N) (6.3 m) = 0

Ilmoitettujen toimintojen suorittaminen:

1262.04 + 352.20 - 3.8T = 0

T: n puhdistaminen saa:

T = 424.8 n

Ensimmäisestä ehdosta sen piti_x = T, siksi:

R -_x = 424.8 n

Kiinnostavia teemoja

Ensimmäinen tasapainon kunto.

Toinen tasapainotila.

Viitteet

1. Bedford, 2000. -Lla. Tekniikan mekaniikka: staattinen. Addison Wesley.
2. Figueroa, D. (2005). Sarja: Tieteen ja tekniikan fysiikka. Osa 4. Hiukkasjärjestelmät. Toimittanut Douglas Figueroa (USB).
3. Giancoli, D.  2006. Fysiikka: sovellusten periaatteet. Kuudes. Ed Prentice Hall.
4. Sears, Zemansky. 2016. Yliopiston fysiikka, jolla on moderni fysiikka. 14. päivä. Ed. Osa 1.
5. Wikipedia. Isostasia. Palautettu: on.Wikipedia.org.