Yhtälöjärjestelmä ratkaisumenetelmät, esimerkit, harjoitukset

Se ekaatiojärjestelmät Ne koostuvat kahdesta tai useammasta yhtälöstä, joissa on useita muuttujia, joilla on oltava yhteinen ratkaisu. Ne ovat usein, koska käytännössä on olemassa lukuisia tilanteita, jotka riippuvat monista tekijöistä, jotka liittyvät monella tavalla.

Yleensä yhtälöjärjestelmässä on seuraava muoto, jossa kukin funktio edustaa yhtä ehdoista, jotka ratkaisun on täytettävä:

Kuvio 1. Yhtälöjärjestelmä koostuu M -toiminnoista ja N tuntemattomista. Lähde: f. Zapata.

Katsotaanpa esimerkkiä: Oletetaan, että sinun on valmistettava suorakaiteen muotoisia paperilevyjä, joiden alue on 180 cm² ja kehä on 54 cm. Mikä olisi arkin mitat?

Vastaamaan kysymykseen otamme huomioon, että suorakaiteen muotoisen arkin mitat ovat kaksi: leveä ja korkea. Tämä tarkoittaa, että meillä on 2 muuttujaa, joihin annamme tavalliset nimet x ja ja.

Ja näiden muuttujien on täytettävä kaksi samaan aikaan asetettua ehtoa:

-Ensimmäinen ehto: Lamina -alue on 180 cm². Tämä on ensimmäinen toiminto: f₁.

-Toinen ehto: arkin kehän tai muodon on oltava 54 cm. Tämä on toinen F -funktio₂.

Jokaiselle ehdoille yhtälö määritetään käyttämällä algebrallista kieltä. Suorakulmaisen arkin alue A saadaan kertomalla leveä:

A = x.y = 180 cm²

Ja kehän P tulokset sivujen lisäämisestä. Koska kehä on sivujen summa:

P = 2x + 2y = 54 cm

Kahdesta yhtälöstä ja kahdesta tuntemattomasta järjestelmästä on: järjestelmä on:

Xy = 180

2 (x + y) = 54

Tarvitsemme kaksi numeroa, joiden tuote on 180 ja että sen summan kaksinkertainen tuote on 54 tai mikä on sama: lisätty on annettava 27. Nämä numerot ovat 12 ja 15.

Ratkaistussa harjoitusosassa tarjoamme yksityiskohtaisen menetelmän näiden arvojen löytämiseksi, sillä välin lukija voi helposti tarkistaa korvaamisen, mikä tyydyttää tehokkaasti molemmat yhtälöt.

[TOC]

Esimerkkejä yhtälöjärjestelmien sovelluksista

Edellä ehdotettu tilanne sisältää 2 muuttujaa, ja niiden löytämiseksi tarvitaan vähintään 2 yhtälöä. On olemassa järjestelmiä, joissa on paljon enemmän muuttujia, mutta joka tapauksessa, jos järjestelmässä on n Näistä ainakin sitä vaaditaan n Riippumattomat yhtälöt (ei voi olla muiden lineaarinen yhdistelmä) ratkaisun löytämiseksi, jos se on olemassa.

Voi palvella sinua: köysi (geometria): pituus, lause ja harjoitukset

Hakemusten suhteen niitä on lukuisia. Tässä on joitain, joissa yhtälöjärjestelmät osoittavat niiden hyödyllisyyden:

-Löydä virtaukset, jotka kiertävät piirin kautta Kirchoffin lakien avulla.

-Maa- ja lentoliikenteessä poistumis- ja saapumisaikataulujen luomiseksi.

-Löydä voimien suuruus dynaamisista tai staattisista järjestelmistä, joihin sovelletaan useita vuorovaikutuksia.

-Tietää tietyn ajanjakson tai tehtaiden myytävien esineiden määrä kohteiden mittojen määrittämiseksi tiettyjen olosuhteiden täyttämiseksi pinnan tai äänenvoimakkuuden suhteen.

-Kun määritetään, kuinka jakaa pääoma useisiin sijoituksiin.

-Luo korot erilaisille palveluille, esimerkiksi televiestintä tai näyttelyitä ja tiedä kerätyn rahan määrän (katso esimerkki ratkaistu 2)

Yhtälöjärjestelmien ratkaisumenetelmät

Menetelmä korvaava

-Valitun yhtälön ja yksi muuttujista puhdistetaan.

-Sitten sinun on vaihdettava selkeä muuttuja toisessa yhtälössä. Sitten tämä muuttuja katoaa sieltä ja jos järjestelmässä on kaksi yhtälöä ja kaksi tuntematonta, on yhtälö, jolla on muuttuja, joka voi olla jo selvä.

-Jos järjestelmässä on enemmän kuin kaksi muuttujaa, sinun on puhdistettava kolmas tuntematon toisesta yhtälöstä ja korvattava se myös.

Esimerkki tämän menetelmän soveltamisesta on vuonna ratkaistu 1.

Vähennys- tai eliminointimenetelmä

Tämä menetelmä koostuu yhtälöiden lisäämisestä tai vähentämisestä yhden tai useamman muuttujan poistamiseksi ja jättäen yksi. Tätä varten on kätevää kertoa yhtälöt tekijällä, että lisäämällä toisella yhtälöllä tuntematon katoaa. Katsotaanpa esimerkkiä:

3x² - ja² = 11

Voi palvella sinua: Ryhmittelemättömän datan keskeiset taipumusmittaukset: Kaavat, harjoitukset

x² + 4y² = 8

Kerroimme ensimmäisen yhtälön 4:

12x² - 4y² = 44

x² + 4y² = 8

Lisäämällä ne tuntematon katoaa ja, Pysyminen:

13x² = 52

x² = 4

Siksi x₁ = 2 ja x₂ = -2. Näillä arvoilla lukija voi varmistaa sen ja₁ = 1 ja₂ = -1

Tasoitusmenetelmä

Kun järjestelmä on kaksi yhtälöä, joissa on kaksi tuntematonta:

-Tuntematon valitaan ja tyhjentää molemmista yhtälöistä.

-Tulokset tasoitetaan, mikä mahdollistaa yhden yhtälön saamisen yhdellä tuntemattomalla.

-Tämä yhtälö on ratkaistu ja tulos korvataan yhdessä aikaisemmista puhdistuksista toisen tuntemattoman arvon saamiseksi.

Tätä menetelmää sovelletaan vuonna seuraavan osan 2 ratkaistaan.

Graafinen menetelmä

Tämä menetelmä koostuu käyrien piirtämisestä, joita kukin yhtälö edustaa. Risteyskohta on järjestelmäratkaisu. Seuraava esimerkki näyttää järjestelmän graafisen ratkaisun:

x² + ja ² = 1

2x + 4y = 0

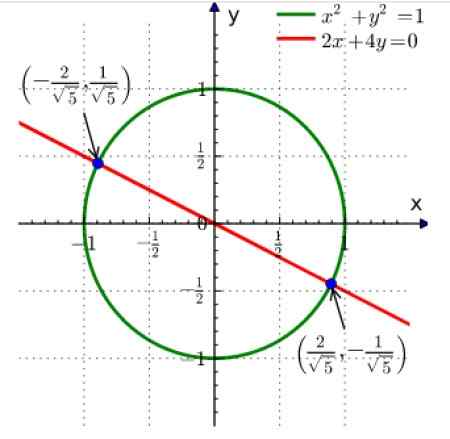Kuva 2. Samanaikaisen yhtälöjärjestelmän graafinen ratkaisu on löytää käyrien leikkauspiste. Lähde: Wikimedia Commons.

Ensimmäinen yhtälöistä on säteen 1 ympyrä, joka keskittyy alkuperään ja toinen on viiva.

Molempien risteys on kaksi pistettä, jotka on esitetty sinisellä. Lukija voi varmistaa, että korvaamalla yllä olevien yhtälöiden pisteiden koordinaatit, tasa -arvo saadaan.

Harjoitukset

- Liikunta ratkaistiin 1

Sinun on valmistettava suorakaiteen muotoisia arkkeja 180 cm: n alueelta² ja 54 cm: n kehällä. Mikä olisi arkin mitat?

Ratkaisu

Ratkaistava järjestelmä on:

Xy = 180

2 (x + y) = 54

Toinen yhtälöä voidaan yksinkertaistaa x + y = 27, siksi:

Xy = 180

x + y = 27

Yksi toisen yhtälön tuntemattomista on puhdistettu:

y = 27 - x

Selvitys korvataan ensimmäisessä:

(27 -x) = 180

Jakavan omaisuuden soveltaminen:

-x² + 27x = 180

Kertomalla (-1) yhtälön molemmilla puolilla ja lähettämällä 180 vasemmalle puolelle:

x² - 27x +180 = 0

Se on toisen asteen yhtälö X: ssä, joka ratkaisee kaava:

Se voi palvella sinua: vastakkaiset kulmat kärjen kautta (ratkaistu harjoitus)

A = 1, b = -27 ja c = 180

 Ratkaisut ovat: x₁ = 15 cm ja x₂ = 12, siten y: n mitat ovat ja₁ = 12 cm ja ja₂ = 15 cm.

- Liikunta ratkaistiin 2

Huvipuistossa on seuraavat hinnat sisäänkäyntiä kohti: lapset 1.5 ja aikuiset 4 dollaria. Yhdessä päivässä kävijöitä oli 2200, keräten 5050 dollaria. Löydä puistossa käynyt lasten ja aikuisten lukumäärä sinä päivänä.

Kuva 3. Yhtälöjärjestelmän tarkoituksena on hajottaa huvipuiston kokoelman päivässä. Lähde: Pixabay.

Ratkaisu

Olla x Lasten lukumäärä ja ja Aikuisten lukumäärä. Voimme luoda ensimmäisen yhtälöistä tietäen, että molempien summan on oltava 2200:

x + y = 2200.

Nyt menemme kerättyjen rahojen mukana. Lasten lipun hinta on 1.5 dollaria jokaisesta lapsesta kertomalla tämä arvo x: llä, lasten lukumäärällä, meillä on määrä lasten sisäänpääsyä varten:

1.5x = lasten lippujen keräämät rahat

Ja jos kerrotaan 4 dollaria aikuista kohden määrästä ja aikuisten kävijöistä, kaikki aikuiset saavat kokonaisrahan:

4y = aikuisten lippujen keräämät rahat

Lisäämme tämän saadaksesi 5050 dollaria:

1.5x + 4y = 5050

Yhtälöjärjestelmämme on:

x + y = 2200

1.5x + 4y = 5050

Ratkaisemme se tasaamalla. Poistamme muuttujan ja ensimmäisen ja toisen yhtälön:

y = 2200 - x

y = (5050 - 1.5 x) /4

Tasaamme molemmat lausekkeet:

2200 - x = (5050 - 1.5x) /4

Kerro kaikki 4: llä murto -osan poistamiseksi:

8800 - 4x = 5050 - 1.5x

Ryhmittelemme termejä X: llä vasemmalla ja oikealla olevilla puhtailla numeroilla:

-4x + 1.5x = 5050 - 8800

-2.5x = -3750

x = 1500 lasta.

Korvaamme tämän arvon y = 2200 - x tuntemaan aikuisten lukumäärän:

y = 2200 - 1500 = 700 aikuista.

Viitteet

1. CK-12. Yhtälö- ja epätasa -arvoiset järjestelmät. Toipunut: CK12.org.
2. Hoffman, J. Matematiikan aiheiden valinta. Nide 2.
3. Jiménez, r. 2008. Algebra. Prentice Hall.
4. Stewart, J. 2006. Precculment: Laskentamatematiikka. Viides. Painos. Cengage -oppiminen.
5. Zill, D. 1984. Algebra ja trigonometria. McGraw Hill.