Johtavuuskaavat, laskelmat, esimerkit, harjoitukset

Se johtokyky Kuljettajalta se on määritelty helpoksi, että sen on kaipattava sähkövirtaa. Se ei riipu pelkästään sen valmistuksessa käytetystä materiaalista, vaan myös sen geometriasta: poikkileikkauksen pituus ja pinta -ala.

Kohtavuuteen käytetty symboli on G, ja se on sähkövastuksen r käänteinen, hiukan tutumpi suuruusluokka. Kansainvälinen järjestelmäyksikkö, jos johtavuutta varten on ohmion käänteinen, nimeltään ω^-1 ja saada nimen Siemens (S).

Kuvio 1. Johtavuus riippuu materiaalista ja kuljettajan geometriasta. Lähde: Pixabay.

Muut sähkössä käytetyt termit, jotka kuulostavat samanlaisilta kuin johtavuus ja liittyvät toisiinsa johtavuus ja ajo, Mutta niitä ei pidä sekoittaa. Ensimmäinen näistä termeistä on sen aineen luontainen ominaisuus, jolla kuljettaja valmistetaan ja toinen kuvaa sähkövarauksen virtausta sen läpi.

Sähköjohtimelle, jolla on jatkuva aluepisteen poikkileikkaus -Lla, pituus Lens ja johtavuus σ, Kohdistavuus antaa:

G = σ.Siihen

Suurempaan johtavuuteen, suurempaan johtavuuteen. Myös mitä suurempi ristikkäinen alue, sitä helpommin kuljettajan antaa nykyinen läpäisy. Päinvastoin, mitä suurempi pituus l, sitä alhaisempi johtavuus, koska nykyiset kantajat menettävät enemmän energiaa pidemmillä matkoilla.

[TOC]

Kuinka johtavuus lasketaan?

Kohtavuus G kapellimestarille, jolla on vakio poikkileikkauspinta -ala, lasketaan yllä annetun yhtälön mukaisesti. Tämä on tärkeää, koska jos poikkileikkaus ei ole vakio, olennaista laskelmaa on käytettävä sekä vastus- että johtavuuden löytämiseen.

Koska se on vastuskohtainen, johtavuus G voidaan laskea tietäen, että:

Voi palvella sinua: Atomin kvantmekaaninen malli

G = 1/r

Itse asiassa kuljettajan sähkövastus voidaan mitata suoraan yleismittarilla, laitteella, joka mittaa myös virtaa ja jännitettä.

Kuljettajat

Kuten alussa todettiin, kansainvälisen järjestelmän johtavuusyksikkö on Siemens (t). Sanotaan.

Katsotaanpa, kuinka se on mahdollista Ohmin lain kautta, jos se on kirjoitettu johtavuuden suhteen:

V = i.R = i/g

Missä V Se on jännite- tai potentiaaliero kuljettajan päiden ja Yllyttää Nykyinen voimakkuus. Näiden suuruuksien suhteen kaava pysyy näin:

G = i/v

Aikaisemmin johtavuusyksikkö oli Mho (ohmi kirjoitettu taaksepäin) merkitty nimellä ʊ, joka on pääoma tai käänteinen omega. Tämä merkintä oli käytössä ja se korvattiin Siemens Saksan insinöörin ja keksijän Ernst von Siemensin (1816-1892) kunniaksi, televiestintäpisaroiden edelläkävijä, mutta molemmat ovat täysin vastaavia.

1 MHO = 1 Siemens = 1 A/V (ampeeri/voltti)

Kuva 2. Johtavuus verrattuna vastustuskykyyn. Lähde: Wikimedia Commons. Think Tank [CC 3: lla.0 (https: // creativecommons.Org/lisenssit/by/3.0)]

Muissa mittausjärjestelmissä Tilastot (tilastot) (CGS: ssä tai senttimetri-gramman sekunnissa) ja ABSIEMENS (ABS) (Sähkömagneettinen CGS -järjestelmä) "S": n lopussa osoittamatta yksikköä tai moniarvoa, koska ne tulevat oikeasta nimestä.

Joitain vastaavuuksia

1 tilasto = 1.11265 x 10 ^-12 Siemens

1 abs = 1 x 10⁹ Siemens

Esimerkit

Kuten aiemmin mainittiin, vastustuskyky, johtavuus tiedetään välittömästi määritettäessä käänteistä tai vastavuoroista arvoa. Tällä tavalla sähkövastus on 100 ohmia, mikä vastaa 0.Esimerkiksi 01 Siemens.

Kaksi muuta esimerkkiä johtavuuden käytöstä:

Voi palvella sinua: magneettinen sokki: yksiköt, kaavat, laskenta, esimerkit

Johtavuus

Ne ovat erilaisia ​​termejä, kuten jo ilmoitettu. Johtavuus on sen aineen ominaisuus, jolla kuljettaja valmistetaan, kun kuljettaja on tyypillinen kuljettajalle.

Johtavuus voidaan ilmaista g: n suhteen:

σ = g.(The)

Seuraavaksi taulukko, jossa on usein käytettyjä johtavia materiaaleja, johtavuus:

pöytä 1. Joidenkin johtimien johtavuus, vastustuskyky ja lämpökerroin. Viitelämpötila: 20 ºC.

Metalli	σ x 106 (Ye)	ρ x 10-8 (Ω.m)	α ºC-1
Hopea	62.9	1.59	0 -.0058
Kupari	56.5	1.77	0 -.0038
Kulta	41.0 -	2.44	0 -.0034
Alumiini	35.4	2.82	0 -.0039
Volframi	18.0 -	5.60 60	0 -.0045
Rauta	10.0 -	10.0 -	0 -.0050

Rinnakkaiset vastukset

Kun niillä on piirejä, joilla on rinnakkaiset resistanssit, joskus on tarpeen saada vastaava vastus. Vastaava vastusarvo mahdollistaa yhden arvon resistenssijoukon korvaamisen.

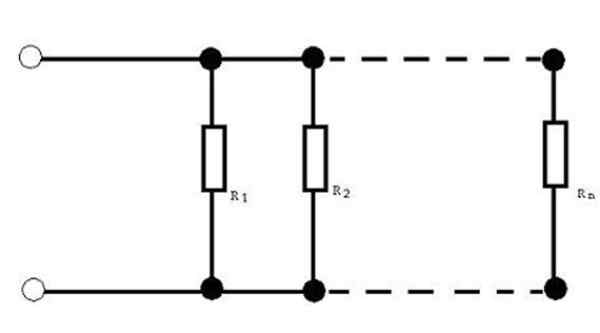Kuva 3. Vastusten assosiaatio rinnakkain. Lähde: Wikimedia Commons. Ei konetta luettavissa olevaa kirjailijaa. Sotake oletettu (tekijänoikeusvaatimusten perusteella). [CC BY-SA 3.0 (http: // creativecommons.Org/lisenssit/by-SA/3.0/]].

Tätä vastuskokoonpanoa varten vastaava vastus annetaan:

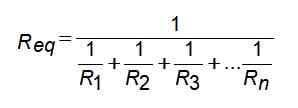
Mutta jos kirjoitat johtavuuden suhteen, se on suuresti yksinkertaistettu: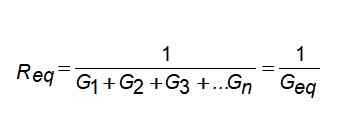Siksi:

G_Eq = G₁ + G₂ + G₃ +... g_n

Toisin sanoen vastaava johtavuus on johtavuuden summa. Jos haluat tietää vastaavan vastarinnan, tulos on yksinkertaisesti sijoitettu.

Harjoitukset

- Harjoitus 1

a) Kirjoita Ohmin laki johtavuuden suhteen.

b) Löydä 5 volframilangan johtavuus 5.4 cm pitkä ja 0.Halkaisija 15 mm.

c) Nyt 1 virta ohitetaan.5 A johdolle. Mikä on potentiaalinen ero tämän kuljettajan päiden välillä?

Voi palvella sinua: 31 fysiikan voimantyyppiä ja niiden ominaisuuksia

Liittää jhk

Edellisistä osioista sinun on:

V = i/g

G = σ.Siihen

Korvaamalla jälkimmäinen ensimmäisessä, se pysyy näin:

V = i /(σ.A/l) = i.L / σ.-Lla

Missä:

-Olen virran voimakkuus.

-L on kuljettajan pituus.

-σ on johtavuus.

-A on poikkileikkauksen alue.

Ratkaisu b

Tämän volframilangan johtavuuden laskemiseksi sen johtavuus vaaditaan, mikä löytyy taulukosta 1:

σ = 18 x10⁶ Tei

L = 5.4 cm = 5.4 x 10^-2 m

D = 0. 15 mm = 0.15 x 10^-3 m

A = π.D -d² / 4 = π . (0.15 x 10^-3 m)² / 4 = 1.77 x 10^-8 m²

Korvaaminen yhtälölläsi:

G = σ.A/L = 18 x10⁶ Tei . 1.77 x 10^-8 m² / 0.15 x 10^-3 M = 2120.6 s.

Liuos C

V = i/g = 1.5 A / 2120.6 s = 0.71 mv.

- Harjoitus 2

Etsi vastaava vastus seuraavasta piiristä ja tietäen, että minä_jompikumpi = 2 a, laske I_x ja piiri häviää teho:

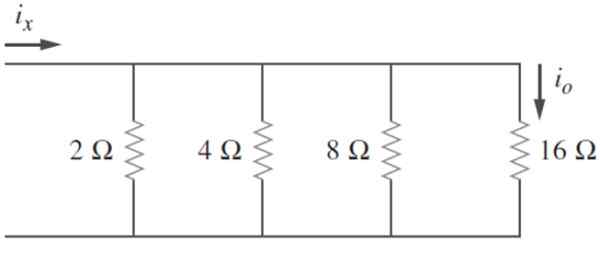Kuva 4. Piiri, jolla on rinnakkaiset vastukset. Lähde: Alexander, c. 2006. Sähköpiirin säätiöt. Kolmas. Painos. McGraw Hill.

Ratkaisu

Resistanssit on lueteltu: r₁= 2 Ω; R -₂= 4 Ω; R -₃= 8 Ω; R -₄= 16 Ω

Sitten johtavuus lasketaan kussakin tapauksessa: g₁ = 0.5 ʊ; G₂ = 0.25 ʊ; G₃ = 0.125 ʊ; G₄ = 0.0625 ʊ

Ja lopuksi ne kasvavat aiemmin osoitetulla tavalla, vastaavan johtavuuden löytämiseksi:

G_Eq = G₁ + G₂ + G₃ +... g_n = 0.5 ʊ + 0.25 ʊ + 0.125 ʊ + 0.0625 ʊ = 0.9375 ʊ

Siksi r_Eq = 1.07 Ω.

Jännite r₄ on v₄ = i_jompikumpi. R -₄ = 2 a . 16 ω = 32 V ja on sama kaikille vastusille, koska ne on kytketty rinnakkain. Sitten on mahdollista löytää virrat, jotka kiertävät kutakin vastustusta varten:

-Yllyttää₁ = V₁ /R₁ = 32 V / 2 ω = 16 a

-Yllyttää₂ = V₂ /R₂ = 32 V / 4 ω = 8 a

-Yllyttää₃ = V₃ /R₃ = 32 V / 8 ω = 4 a

-Yllyttää_x = i₁ +  Yllyttää₂ +  Yllyttää₃ + Yllyttää_jompikumpi = 16 + 8 + 4 + 2 a = 30 a

Lopuksi, hävitetty voima P on:

P = (i_x-A². R -_Eq = 30 - x 1.07 ω = 32.1 W

Viitteet

1. Alexander, c. 2006. Sähköpiirin säätiöt. Kolmas. Painos. McGraw Hill.
2. Megaampere / millivolt Absiemens -laskimen muuntamiseen. Toipunut: Pinkbird.org.
3. Garcia, L. 2014. Sähkömagnetismi. Toinen. Painos. Santanderin teollisuusyliopisto. Kolumbia.
4. Ritari, r.  2017. Tutkijoiden fysiikka ja tekniikka: strategialähestymistapa.  Pearson.
5. Rulla, D. 1990. Fyysinen. Sähkö, magnetismi ja optiikka. Osa II. Toimitus palautti.
6. Wikipedia. Sähkönjohtavuus. Palautettu: on.Wikipedia.org.
7. Wikipedia. Siemens. Palautettu: on.Wikipedia.org.