Ohmin laki ja kaava, laskelma, esimerkit, harjoitukset

Se Ohmin laki, Makroskooppisessa muodossaan se osoittaa, että virran jännite piirissä ovat suoraan verrannollisia, vastus on suhteellisuusvakio. OHM: n laki osoittaa, että nämä kolme suuruutta, kuten V, I ja R, osoittaa, että: V = i.R -.

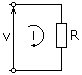
Samoin Ohmin laki on yleinen sisältämään piirielementtejä, jotka eivät ole puhtaasti resistiivisiä vuorotellen virran piireissä, joten se hyväksyy seuraavasti: V = i. Z -z.

Kuvio 1. Ohmin lakia voidaan soveltaa moniin piireihin. Lähde: Wikimedia Commons. Tlapicka [cc by-Sa 3.0 (https: // creativecommons.Org/lisenssit/by-SA/3.0)]

Missä Z -z Se on impedanssi, joka edustaa myös vuorottelevan virran kulkua piirielementillä, esimerkiksi lauhduttimella tai induktanssilla.

On huomattava, että kaikki piirimateriaalit ja elementit eivät ole Ohmin lain mukaisia. Niille, joissa se on pätevä ohminen, Ja jossa sitä ei täytetä, niitä kutsutaan Ei-ohminen tai epälineaarinen.

Yleiset sähkövastukset ovat ohmia, mutta diodit ja transistorit eivät ole, koska jännitteen ja virran välinen suhde ei ole lineaarinen.

Ohmin laki on hänen nimensä velkaa saksalaiselle fyysikoille ja matemaattiselle. Hänen kunniakseen on nimitetty kansainvälisen järjestelmän sähkövastuksen yksikkö: ohmi, joka ilmaistaan ​​myös kreikkalaisella kirjaimella ω ω.

[TOC]

Kuinka se lasketaan?

Vaikka OHM: n lain makroskooppinen muoto on tunnetuin, koska se yhdistää määrät, jotka ovat helposti mitattavissa laboratoriossa, Mikroskooppinen muoto liittyy kaksi tärkeää vektorimäärää: sähkökenttä JA ja virrantiheys J --

J - = σ.JA

Jos σ on materiaalin sähkönjohtavuus, ominaisuus, joka osoittaa sen helppoutta ohjata virtaa. Omalta osaltaan J - Se on vektori, jonka suuruus on merkintä nykyisen intensiteetin I ja sen poikkileikkauksen pinta -alan, jota se kiertää.

Se voi palvella sinua: pinnalliset aallot: ominaisuudet, tyypit ja esimerkit

On loogista olettaa, että materiaalin sisällä olevan sähkökentän ja sen läpi kiertävän sähkövirran välillä on luonnollinen yhteys.

Mutta virta ei ole vektori, koska sillä ei ole osoitetta avaruudessa. Sen sijaan vektori J - Se on kohtisuorassa - tai normaali - kuljettajan ristikkäinen alue, ja sen merkitys on virran alue.

Tästä OHM: n lain muodosta saavutetaan ensimmäinen yhtälö, olettaen, että pituusohjain ja poikkileikkaus A, ja korvaamalla suuruus J - ja JA Lähettäjä:

J = i/a

E = v/ℓ

J = σ.E → i/a = σ. (V/ℓ)

V = (ℓ/σ.To).Yllyttää

Käänteistä kutsutaan vastustuskyky Ja se on merkitty kreikkalaisella kirjaimella ρ:

1/ σ = ρ

Siksi:

V = (ρℓ/ a).I = r.Yllyttää

Kuljettajan vastus

Yhtälössä V = (ρℓ/ a).Yllyttää, Vakio (ρℓ/ a) Siksi se on vastustuskyky:

R = ρℓ/ a

Kuljettajan vastus riippuu kolmesta tekijästä:

-Hänen resistiivisyys ρ, tyypillinen materiaalille, jolla hän on valmistettu.

-Pituus ℓ.

-Sen poikkileikkauksen alue A.

Suurempi ℓ, suurempi vastus, koska nykyisillä kantajilla on enemmän mahdollisuuksia törmätä muiden kuljettajan sisällä olevien hiukkasten kanssa ja menettää energiaa. Ja päinvastoin, suurempaan a, nykyisten operaattoreiden on helpompi liikkua järjestettävällä tavalla materiaalin avulla.

Lopuksi kunkin materiaalin molekyylirakenteessa on helppous, jolla aine antaa sähkövirran passin. Siten esimerkiksi metallit, kuten kupari, kulta, hopea ja platina, joilla on alhainen resistiivisyys, ovat hyviä johtimia, kun taas puu, kumi ja öljy eivät ole, joten niillä on suurempi resistiivisyys.

Esimerkit

Tässä on kaksi havainnollistavaa esimerkkiä Ohmin laista.

Kokeile tarkistaaksesi Ohmin lain

Yksinkertainen kokemus kuvaa Ohmin lakia, tälle tarvitaan pala johtavasta materiaalista, muuttuva jännitelähde ja yleismittari.

Voi palvella sinua: painomittarit

Johtavan materiaalin päiden joukossa vahvistetaan jännite V, joka tulisi vaihdella vähitellen. Muuttuvan virtalähteen avulla voidaan kiinnittää mainitun jännitteen arvot, jotka mitataan yleismittarilla, samoin kuin kuljettajan kiertämä virta.

Arvojen V ja I pariskunnat tallennetaan taulukkoon ja niiden kanssa rakennetaan millimetripaperi -kuvaaja. Jos tuloksena oleva käyrä on viiva, materiaali on ohminen, mutta jos se on muuta käyrää, materiaali ei ole -oHminen.

Ensimmäisessä tapauksessa linjan kaltevuus voidaan määrittää, mikä vastaa kuljettajan vastustusta tai sen käänteistä, johtavuutta.

Seuraavassa kuvassa sininen viiva edustaa yhtä näistä grafiikoista ohmiselle materiaalille. Sillä välin keltaiset ja punaiset käyrät ovat esimerkiksi ei-iskmisiä materiaaleja, kuten puolijohde,.

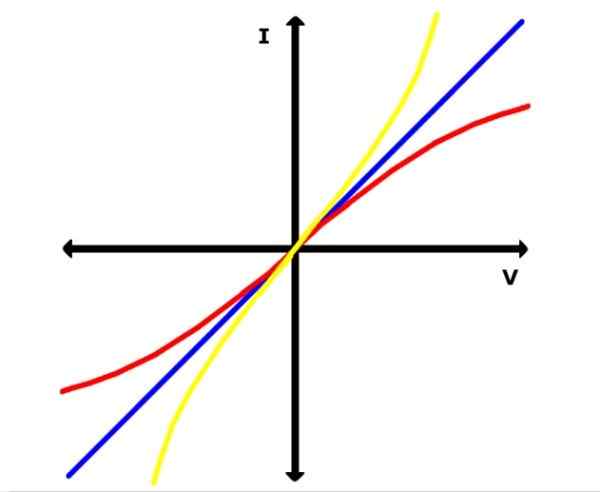Kuva 2. Kaavio I Vs. V ohmimateriaaleille (sininen suora) ja ei-olosohmisille materiaaleille. Lähde: Wikimedia Commons.

Ohmin lain hydraulinen analogia

On mielenkiintoista tietää, että OHM -lain sähkövirralla on samanlainen käyttäytyminen tietyllä tavalla putken läpi kiertävän veden. Englantilainen fyysikko Oliver Lodge ehdotti ensimmäisenä nykyisen käyttäytymisen simulointia hydraulisten elementtien kautta.

Esimerkiksi putket edustavat johtimia, koska vesi kiertää niiden ja nykyisten kantajien läpi viimeisen läpi. Kun putkessa on kapenevaa, vedenkulku on vaikeaa, joten tämä vastaa sähkövastusta.

Paineero putken kahdessa päissä sallii veden virtauksen, joka tarjoaa korkeuden tai vesipumpun eron, ja analogisesti potentiaaliero (akku) on se, joka pitää liikkuvan kuorman, joka vastaa virtausta tai tilavuutta Vesi aikayksikköä kohti.

Se voi palvella sinua: Konvektion lämmönsiirto (esimerkeillä)

Männän pumppu edustaa vaihtoehtoisen jännitteen lähteen roolia, mutta vesipumpun asettamisen etuna on, että hydraulipiiri suljetaan, koska sähköpiiri tulisi olla virtausvirta.

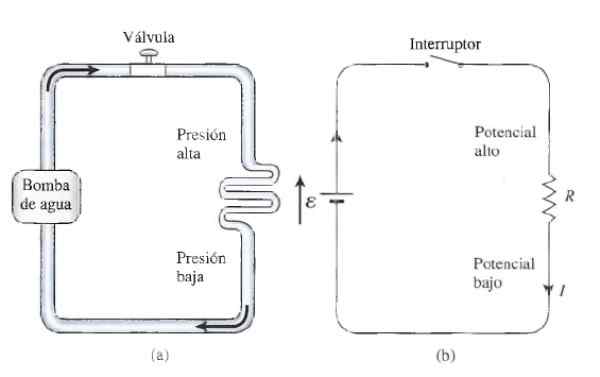Kuva 3. Hydraulinen analogia Ohm -laki: A) veden virtausjärjestelmässä ja b) yksinkertainen resistiivinen piiri. Lähde: Tippens, P. 2011. Fysiikka: Käsitteet ja sovellukset. 7. painos. McGraw Hill.

Vastus- ja kytkimet

Kytkimen vastine olisi kulkunäppäin. Sitä tulkitaan tällä tavalla: jos piiri on auki (suljettu kohta), virta ja vesi eivät voi virtata.

Toisaalta suljetun kytkimen (täysin avoin askel -avain) sekä virta että vesi voivat kiertää ilman ongelmia kuljettajan tai putken avulla.

Kulkunäppäin tai venttiili voi myös edustaa vastusta: Kun avain avautuu kokonaan, se vastaa kuin nollaskestävyys tai oikosulku. Jos se sulkeutuu ollenkaan, se on kuin avoin piiri osittain suljettuna, se on kuin tietyn arvon vastus (katso kuva 3).

Harjoitukset

- Harjoitus 1

Tiedetään, että sähkölevy vaatii 2 A: n 120 V: n toimimiseksi kunnolla. Mikä on sinun vastus?

Ratkaisu

Resistanssi puhdistetaan Ohmin laista:

R = V/ i = 120 V/ 2 A = 60 Ω

- Harjoitus 2

3 mm: n halkaisijaltaan ja 150 m pitkään on 3 3.00 Ω 20 ° C: ssa. Löydä materiaalin resistiivisyys.

Ratkaisu

Yhtälö R = ρℓ/ a on sopiva, Siksi on välttämätöntä löytää poikkileikkauksen alue:

A = π(D/2)² = π (3 x 10^-3 M/2)² = 4.5π x 10 ^-6 m²

Lopuksi vaihdettaessa saat:

ρ = a.R /ℓ = 4.5π x 10 ^-6 m² x 3 Ω / 150 m = 2.83 x 10 ^-7 Ω.m

Viitteet

1. Resnick, r. 1992.Fyysinen. Kolmas painos laajennettu espanjaksi. Nide 2. Mannertoimitusyhtiö S.-Lla. C: n.V.
2. Sears, Zemansky. 2016. Yliopiston fysiikka, jolla on moderni fysiikka. 14^th. Ed. Nide 2. 817-820.
3. Serway, R., Jewett, J. 2009. Tiede- ja tekniikkafysiikka modernin fysiikan kanssa. 7. painos. Nide 2. Cengage -oppiminen. 752-775.
4. Tippens, P. 2011. Fysiikka: Käsitteet ja sovellukset. 7. painos. McGraw Hill.
5. Sevillan yliopisto. Sovelletun fysiikan laitos III. Tiheys ja virran voimakkuus. Toipunut: meistä.On.
6. Walker, J. 2008. Fysiikka. 4. ed. Pearson.725-728