Congruence Congruent -hahmot, kriteerit, esimerkit, harjoitukset

Se kongruenssi, Geometriassa hän huomauttaa, että jos kahdella litteällä hahmolla on sama muoto ja mitat, nämä ovat yhdenmukaisia. Esimerkiksi kaksi segmenttiä ovat yhdenmukaisia, kun niiden pituudet ovat yhtä suuret. Myös yhtenäisillä kulmilla on sama mitta, vaikka ne eivät ole suunnattu samalla tavalla koneessa.

Termi "kongruenssi" tulee latinaksi Kongruentia, jonka merkitys on kirjeenvaihto. Siten kaksi yhdenmukaista lukua vastaa tarkalleen yhtä toisen kanssa.

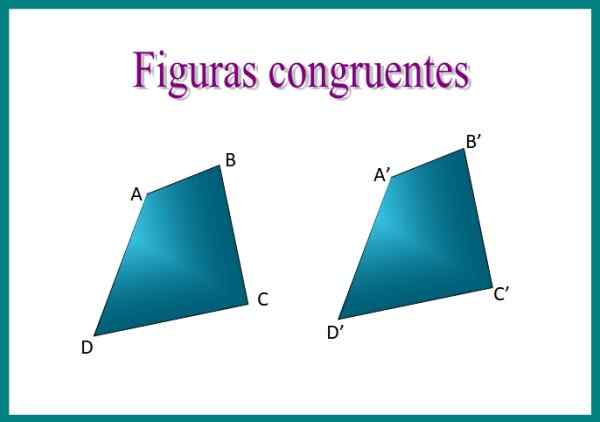
Kuvio 1. Kuvan kvadrilateriaalit ja a'b'c'd 'ovat yhteneviä: heidän sivuillaan on sama mitta, samoin kuin heidän sisäkulmat. Lähde: f. Zapata.

Esimerkiksi, jos olemme päällekkäin kuvan kahta neljännestervettä, huomaat, että ne ovat yhdenmukaisia, koska heidän sivujensa sijoittaminen on identtistä ja ne mittaavat saman.

Kun sijoitat neljänneksen abcd ja a'b'c'd 'toisaalta, luvut vastaavat täsmälleen. Vastaavia sivuja kutsutaan homologiset puolet jompikumpi vastaava Ja ilmaista kongruenssi Symbolia ≡ käytetään. Sitten voimme sanoa, että abcd ≡ a'b'c'd '.

[TOC]

Kongruenssikriteerit

Seuraavat ominaisuudet ovat yhteisiä yhtenäisille monikulmoille:

-Yhtä muotoinen ja koko.

-Identtiset mittaukset näkökulmistasi.

-Samassa määrin sen sivuilla.

Jos kaksi kyseistä monikulmioonia on säännöllisiä, ts. Kaikki osapuolet ja sisäkulmat mittaavat saman, yhtenäisyys varmistetaan, kun yksi seuraavista olosuhteista täyttyy:

-Osapuolet ovat yhdenmukaisia

-Se apothemit olla sama mitta

-Hän radio kunkin monikulmion mitat ovat samat

Säännöllisen monikulmion apoteeme on keskustan ja yhden sivun välinen etäisyys, kun taas säde vastaa etäisyyttä keskustan ja kuvion kärjen tai kulman välillä.

Kongruenssikriteerejä käytetään usein, koska monia osia ja kappaleita on valmistettu sarjassa, ja niiden on oltava sama muoto ja mitat. Tällä tavalla ne voidaan helposti vaihtaa tarvittaessa, esimerkiksi mutterit, ruuvit, arkit tai maan mukulakivet kadulla.

Voi palvella sinua: Simpson -sääntö: kaava, esittely, esimerkit, harjoituksetKuva 2. Katu mukulakivet ovat yhdenmukaisia ​​hahmoja, koska niiden muoto ja mitat ovat täsmälleen samat, vaikka niiden suunta lattialle voi muuttua. Lähde: Pixabay.

Kongruenssi, identiteetti ja samankaltaisuus

Esimerkiksi kongruenssiin liittyy geometrisiä käsitteitä Identtiset luvut ja samanlaisia ​​lukuja, jotka eivät välttämättä tarkoita, että luvut ovat yhdenmukaisia.

Huomaa, että yhdenmukaiset luvut ovat identtisiä, mutta kuvion 1 nelikulmaiset voitaisiin suuntautua eri tavoin lentokoneessa ja edelleen olla yhteneväinen, koska erilainen suunta ei muuta niiden sivujen tai niiden kulmien kokoa. Tässä tapauksessa he lakkaavat olemasta identtinen.

Toinen käsite on lukujen samankaltaisuus: kaksi litteää lukua on samanlainen, jos niillä on sama muoto ja niiden sisäkulmat mittaavat samat, vaikka kuvioiden koko voi olla erilainen. Jos näin on, luvut eivät ole yhdenmukaisia.

Kongruenssiesimerkit

- Kulmien yhtenäinen

Kuten alussa ilmoitimme, yhtenäisillä kulmilla on sama mitta. Yhteyskulmien hankkimiseksi on useita tapoja:

Esimerkki 1

Kaksi viivaa, joissa on yhteinen piste, määrittelevät kaksi kulmaa, joita kutsutaan Vastakkaiset kulmat kärjen vieressä. Näillä kulmilla on sama toimenpide, siksi ne ovat yhdenmukaisia.

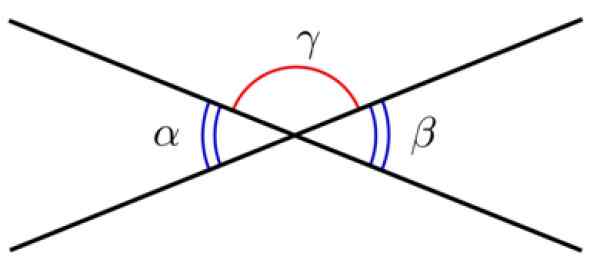Kuva 3. Vastakkaiset kulmat kärjen vieressä. Lähde: Wikimedia Commons.

Esimerkki 2

On kaksi rinnakkaista viivaa ja viiva t se leikkaa ne molemmat. Kuten edellisessä esimerkissä, kun tämä viiva leikkaa rinnakkaiset, se tuottaa yhdenmukaisia ​​kulmia, yksi jokaiselle riville oikealle puolelle ja kaksi muuta vasemmalla puolella. Kuvio näyttää α ja α₁, linjan oikealla puolella t, He ovat yhdenmukaisia.

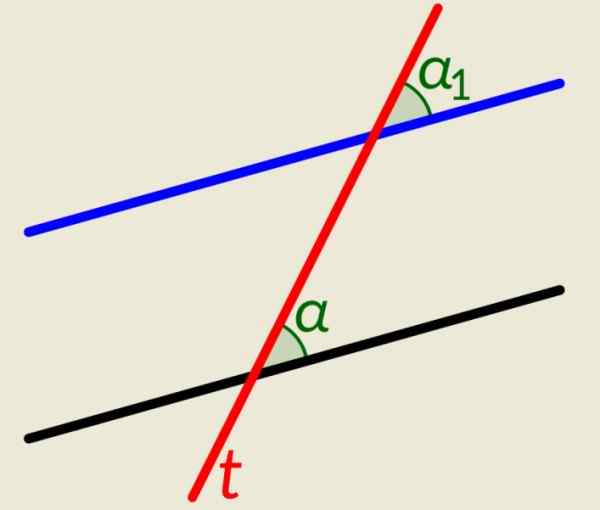Kuva 4. Kuvassa esitetyt kulmat ovat yhdenmukaisia. Lähde: Wikimedia Commons. Lfahlberg/cc by-sa (https: // creativecommons.Org/lisenssit/by-SA/3.0).

Esimerkki 3

Parallelogrammissa on neljä sisäkulmaa, jotka ovat yhdenmukaisia ​​kahdesta kahteen. Ne ovat vastakkaisia ​​kärkipisteitä, kuten seuraavassa kuvassa esitetään, joissa kaksi vihreää kulmaa ovat yhdenmukaisia, samoin kuin kaksi kulmaa punaisella.

Voi palvella sinua: Acutlangle Triangle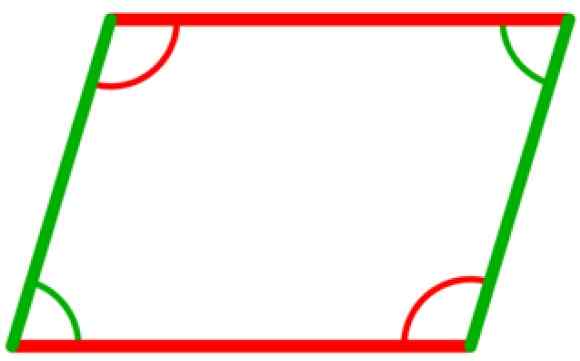Kuva 5. Rinnakkaisogrammin sisäkulmat ovat yhdenmukaisia ​​kahteen kahteen. Lähde: Wikimedia Commons.

- Kolmioiden yhtenäisyys

Kaksi identtistä ja saman kokoista kolmiota ovat yhdenmukaisia. Tämän varmistamiseksi on olemassa kolme kriteeriä, joita voidaan tutkia yhtenäisyyden etsiessä:

-LLL -kriteerit: Kolmioiden kolmella puolella on samat toimenpiteet, siksi L₁ = L '₁; Lens₂ = L '₂ ja minä₃ = L '_3.

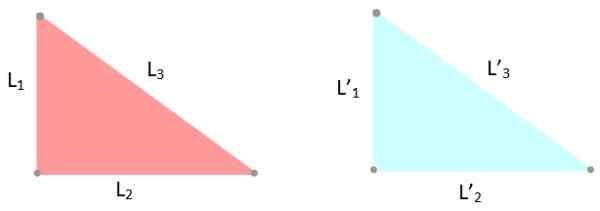Kuva 6. Esimerkki kongruentista kolmioista, joiden puolet mittaavat saman. Lähde: f. Zapata.

-Kriteerit yksi: Kolmioilla on kaksi yhtä suurta sisäkulmaa ja näiden kulmien välisellä sivulla on sama mitta.

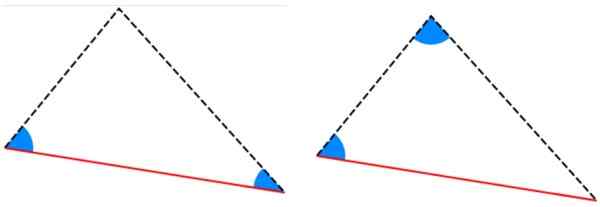Kuva 7. Kriteerit Ala ja Aal kolmioiden yhtenäisyydelle. Lähde: Wikimedia Commons.

-LAL -kriteerit: Kaksi sivua on identtiset (vastaavat) ja niiden joukossa on sama kulma.

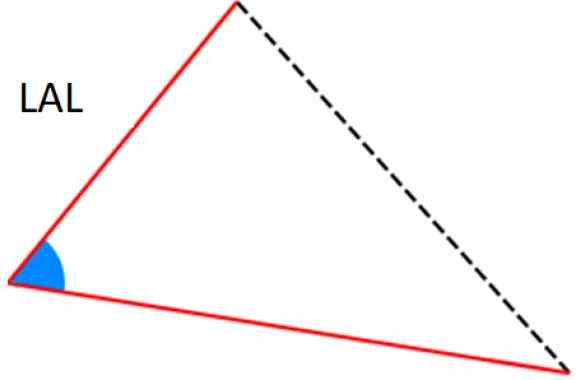Kuva 8. LAL -kriteerit kolmioiden yhtenäisyydestä. Lähde: Wikimedia Commons.

Ratkaisut

- Harjoitus 1

Seuraavassa kuviossa on esitetty kaksi kolmiota: ΔABC ja ΔECF. Tiedetään, että ac = ef, että ab = 6 ja vrt. = 10. Lisäksi kulmat ∡bac ja ∡fec ovat yhdenmukaisia ​​ja myös kulmat ∡acb ja ∡fcb ovat.

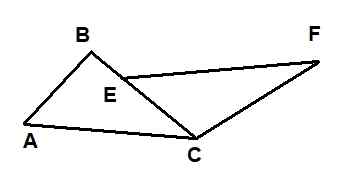Kuva 9. Esimerkin kolmiot ratkaistiin 1. Lähde: f. Zapata.

Sitten segmentin pituus on yhtä suuri kuin:

(i) 5 

(Ii) 3

(Iii) 4 

(Iv) 2

(v) 6

Ratkaisu

Koska kahdessa kolmiossa on yhtä pitkäaikaisia ​​AC = EF -puolia yhtäläisten kulmien välillä ∡Bac = ∡CEF ja ∡BCA = ∡CFE, voidaan sanoa, että kaksi kolmiota ovat kongruenttikriteerien mukaan.

Se on ΔBac ≡ ΔCef, joten sinun on:

Ba = CE = AB = 6

BC = CF = 10

AC = EF

Mutta segmentti, jonka haluat laskea, on = BC - EC = 10 - 6 = 4.

Niin että oikea vastaus on (iii).

- Harjoitus 2

Kuvassa on esitetty kolme kolmiota. On myös tiedossa, että kaksi osoitettua kulmaa mittaavat kumpikin 80º ja että segmentit ab = pd ja ap = cd. Etsi kuvassa ilmoitettu kulman X arvo.

Se voi palvella sinua: Polybal -grafiikka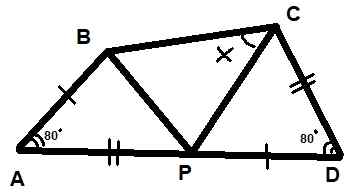Kuva 10. Kolmiot esimerkille ratkaistu 2. Lähde: f. Zapata.

Ratkaisu

Sinun on käytettävä kolmioiden ominaisuuksia, jotka ovat yksityiskohtaisia ​​askel askeleelta.

Vaihe 1

Alkaen LAL -kolmioiden yhdenmukaistamiskriteeristä voidaan sanoa, että BAP- ja PDC -kolmiot ovat yhdenmukaisia:

ΔBAP ≡ ΔPDC

Vaihe 2

Yllä oleva johtaa vakuuttamaan, että bp = PC, siksi kolmio ΔBPC on sammal ja ∡pcb = ∡pbc = x.

Vaihe 3

Jos kutsumme γ BPC -kulmaan, seuraa sitä:

2x + γ = 180º

Vaihe 4

Ja jos kutsumme β: ta APB- ja DCP- ja α -kulmiksi ABP- ja DPC -kulmiin, sen on:

α + β + γ = 180º (koska APB on tasainen kulma).

Vaihe 5

Lisäksi a + β + 80º = 180º APB -kolmion sisäkulmien summalla.

Vaihe 6

Yhdistämällä kaikki nämä lausekkeet, jotka sinun on:

α + β = 100º

Vaihe 7

Ja siksi:

γ = 80º.

Vaihe 8

Lopuksi seuraa, että:

2x + 80º = 180º

X = 50º: n kanssa.

Viitteet

1. Baldor, a. 1973.Litteä ja avaruusgeometria. Keski -Amerikan kulttuuri-.
2. CK-12-säätiö. Yhtenäiset monikulmiot. Haettu osoitteesta: CK 12.org.
3. Nauti matematiikasta. Määritelmät: Radio (Polygon). Toipunut.com.
4. Matematiikan avoin viite. Testaus monikulmioiden kongruenssi. Toipunut: MathPenref.com.
5. Wikipedia. Kongruenssi (geometria). Palautettu: on.Wikipedia.org.
6. Zapata, f. Kolmiot, historia, elementit, luokittelu, ominaisuudet. Haettu: Lifer.com.