Integraatiovakio merkitys, laskenta ja esimerkit

Se Integraatiovakio Se on lisäarvo antidervatiivien tai integraalien laskemiseen, se edustaa ratkaisuja, jotka muodostavat funktion primitiivisen. Ilmaisee luontaisen epäselvyyden, jos jollain funktiolla on ääretön määrä primitiivistä.

Esimerkiksi, jos funktio otetaan: f (x) = 2x + 1 ja saamme sen antiDative:

∫ (2x+1) dx = x² + x + C ; Missä C Se on Integraatiovakio ja edustaa graafisesti pystysuuntaista käännöstä primitiivisten äärettömien mahdollisuuksien välillä. On oikein sanoa, että (x² + x) se on eräs primitiivisen f (x).

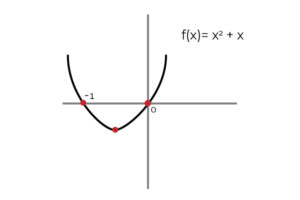Lähde: Kirjoittaja

Samalla tavalla voit määritellä (x² + x + C ) f (x): n primitiivinä.

[TOC]

Käänteinen ominaisuus

Voidaan huomata, että lausekkeen johdettaessa (x² + x) funktio f (x) = 2x + 1 saadaan. Tämä johtuu käänteisestä ominaisuudesta johdannaisen ja toimintojen integroinnin välillä. Tämä ominaisuus mahdollistaa integraatiokaavojen hankkimisen erottelusta alkaen. Joka mahdollistaa integraalien todentamisen samojen johdannaisten kautta.

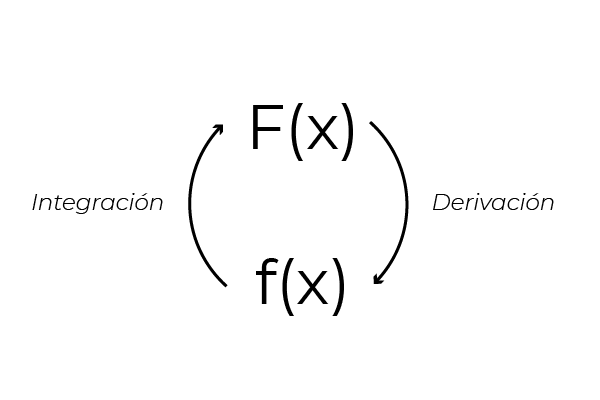Lähde: Kirjoittaja

Kuitenkin (x² + x) Se ei ole ainoa funktio, jonka johdannainen on yhtä suuri kuin (2x + 1).

1. D (x² + x)/ dx = 2x + 1
2. D (x² + x + 1)/ dx = 2x + 1
3. D (x² + x + 2)/ dx = 2x + 1
4. D (x² + x + 3)/ dx = 2x + 1
5. D (x² + x + C)/ dx = 2x + 1

Missä 1, 2, 3 ja 4 edustavat erityistä primitiivistä f (x) = 2x + 1. Kun taas 5 edustaa F (x) = 2x + 1: n määrittelemätöntä tai primitiivistä integraalia.

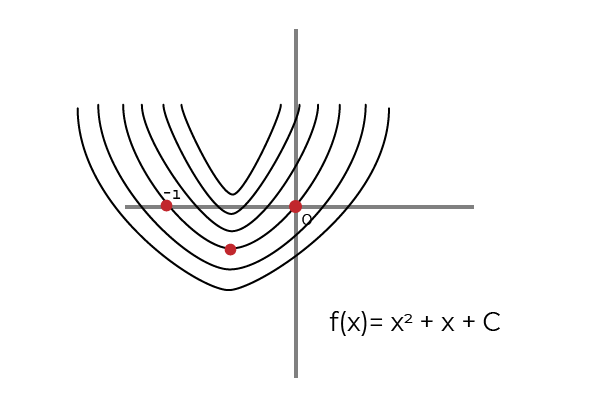Lähde: Kirjoittaja

Funktion primitiivi saavutetaan antiidernivoinnin tai kiinteän prosessin avulla. Missä f on primitiivinen f, jos seuraava on toteutettu

• y = ∫ f (x) dx = F (x) + c; C = Integraatiovakio
• F '(x) = f (x)

On ymmärrettävä, että funktiolla on yksi johdannainen, toisin kuin sen ääretön primitiivinen, joka johtuu integraatiosta.

Määrittelemätön integraali

 ∫ f (x) dx = f (x) + c

Se vastaa saman kuvion käyriä, jotka kokevat epäjohdonmukaisuuden kunkin pisteen kuvien arvossa (x, y). Jokainen tämän kuvion täyttävä toiminto on yksittäinen primitiivinen ja kaikkien toimintojen joukko tunnetaan nimellä Määrittelemätön integraali.

Arvon Integraatiovakio Se erottaa jokaisen toiminnon käytännössä.

Se Integraatiovakio Se ehdottaa pystysuuntaista siirtymistä kaikissa kaavioissa, jotka edustavat funktion primitiivistä. Missä niiden välillä havaitaan rinnakkaisuus ja tosiasia C Se on siirtymän arvo.

Yleisten käytäntöjen mukaan Integraatiovakio Se on merkitty kirjaimella “C” lisäyksen jälkeen, vaikka käytännössä se on välinpitämätöntä, jos vakio lisää tai vähenee. Sen todellinen arvo löytyy eri tavoin eri tavoin alkuolosuhteet.

Integraatiovakion muut merkitykset

Oli jo puhetta miten Integraatiovakio sovelletaan kiinteä laskenta; Edustaa käyriä, jotka määrittelevät määrittelemättömän integroinnin. Mutta monet muut tieteet ja oksat ovat osoittaneet erittäin mielenkiintoisia ja käytännöllisiä arvoja Integraatiovakio, jotka ovat helpottaneet useiden tutkimusten kehittämistä.

Voi palvella sinua: suorakulmio Trapezoid: Ominaisuudet, suhteet ja kaavat, esimerkit

Siinä fyysinen Integraatiovakio voi ottaa useita arvoja tietojen luonteen mukaan. Hyvin yleinen esimerkki on tuntea funktio V (t) joka edustaa nopeus hiukkasen verrattuna aika t. Tiedetään, että alkeellista v (t) laskettaessa funktio saadaan R (t) joka edustaa sijainti hiukkasen verrattuna.

Se Integraatiovakio edustaa alkuperäisen sijainnin arvoa, toisin sanoen tällä hetkellä T = 0.

Samoin, jos funktio tunnetaan A (t)  joka edustaa kiihtyvyys hiukkasen verrattuna. A (t): n primitiivi johtaa funktioon v (t), missä Integraatiovakio Se on alkuperäisen nopeuden V arvo_{0 -}.

Siinä talous, hankkimalla kustannusfunktion primitiivi integroimalla. Se Integraatiovakio edustaa kiinteitä kustannuksia. Ja niin monia muita sovelluksia, jotka ansaitsevat differentiaali- ja kiinteät laskelmat.

Kuinka integraatiovakio lasketaan?

Laskemiseksi Integraatiovakio, On aina tarpeen tietää alkuolosuhteet. Jotka ovat vastuussa siitä, mikä mahdollisista primitiivisistä on vastaava.

Monissa sovelluksissa sitä käsitellään riippumattomana muuttujana ajaksi (t), missä vakio C Ota arvot, jotka määrittelevät alkuolosuhteet erityistä tapausta.

Jos alkuperäinen esimerkki otetaan: ∫ (2x+1) dx = x² + x + C

Kelvollinen alkuedellytys voi olla grafiikan ehto tietyn koordinaatin läpi. Esimerkiksi tiedetään, että primitiivinen (x² + x + C) Käy läpi pisteen (1, 2)

F (x) = x² + x + C; Tämä on yleinen ratkaisu

F (1) = 2

Korvaamme tämän tasa -arvon yleisen ratkaisun

F (1) = (1)² + (1) + c = 2

Missä se on helppo päätellä C = 0

Tällä tavalla vastaava primitiivinen tapaus on F (x) = x² + x

On olemassa erityyppisiä numeerisia harjoituksia, jotka toimivat Integraatiovakiot. Itse asiassa differentiaali- ja kiinteä laskenta ei lopeta soveltamista nykyisissä tutkimuksissa. Eri akateemisilla tasoilla löydät; Alkuperäisestä laskelmasta, fysiikan, kemian, biologian, talouden kautta, muun muassa.

Sitä arvostetaan myös tutkimuksessa differentiaaliyhtälöt, missä Integraatiovakio Voit ottaa erilaisia ​​arvoja ja ratkaisuja, jotka johtuvat tässä asiassa suoritetuista monista viitteistä ja integraatioista.

Esimerkit

Esimerkki 1

1. Tykki sijaitsee 30 metrin korkeissa versoilla pystysuoraan ammukseen. On tiedossa, että alkuperäinen ammuksen nopeus on 25 m/s. Päättää:

• Toiminto, joka määrittelee ammuksen sijainnin ajan suhteen.
• Lentoaika tai aika, jolloin hiukkanen pelaa.

Se voi palvella sinua: 8 tyyppiä mittausvirheitä (esimerkkien kanssa)

On tiedossa, että tasaisesti monipuolisesti suorakulmaisen liikkeen kiihtyvyys on vakioarvo. Näin on ammuksen lanseeraus, jossa kiihtyvyys on painovoima

G = - 10 m/s²

On myös tiedossa, että kiihtyvyys on toinen sijainnista johdettu, mikä osoittaa kaksinkertaisen integraation harjoituksen resoluutioon, mikä saa kaksi Integraatiovakiot.

A (t) = -10

V (t) = ∫a (t) dt = ∫ (-10t) dt = -10t + C₁

Harjoituksen alkuolosuhteet osoittavat, että alkuperäinen nopeus on v_{0 -} = 25 m/s. Tämä on nopeus ajankohtana t = 0. Tällä tavalla on toteutettu, että:

V (0) = 25 = -10 (0) + C₁   ja C₁ = 25

Määritettävä nopeusfunktio

V (t) = -10t + 25; Voit nähdä samankaltaisuuden MRUV -kaavan kanssa (V_F = V_{0 -} + A x t)

Homologisessa nopeusfunktiossa on integroitu ilmaisun saavuttamiseksi, joka määrittelee sijainnin:

R (t) = ∫v (t) dt = ∫ (-10t+25) dt = -5t² + 25T + C₂

R (t) = -5T² + 25T + C₂  (Primitiivinen sijainti)

Alkuasento r (0) = 30 m tunnetaan. Silloin ammuksen erityinen primitiivinen lasketaan.

R (0) = 30m = -5 (0)² + 25 (0) + C₂ . Missä C₂ = 30

Ensimmäinen osa on ratkaistu siitä lähtien R (t) = -5T² + 25T + 30  ; Tämä ekspressio on homologinen siirtymäkaavassa MRUV R (T) = R_{0 -} + V_{0 -}T - GT²/2

Toisessa osassa neliömäinen yhtälö on ratkaistava: -5T² + 25T + 30 = 0

Koska se ehdottaa hiukkasia saavuttamaan maan (sijainti = 0)

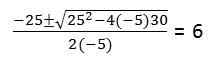Lähde: Kirjoittaja

Oikeastaan ​​toisen luokan yhtälö heittää 2 ratkaisua t: 6, -1. Arvo t = -1 jätetään huomiotta, koska nämä ovat ajan yksiköitä, joiden verkkotunnus ei sisällä negatiivisia lukuja.

Tällä tavalla toinen osa, jossa lentoaika on yhtä suuri kuin 6 sekuntia, on ratkaistu.

Esimerkki 2

2. Löydä alkuolosuhteet vastaava primitiivinen F (x):

• f "(x) = 4; f '(2) = 2; f (0) = 7

Toisen johdannaisen F "(x) = 4 antitointiprosessi alkaa

f '(x) = ∫f "(x) dx

∫4 dx = 4x + c₁

Sitten, kun tiedät kunto f '(2) = 2 etenee:

4 (2) + C₁ = 2

C₁ = -6 ja f '(x) = 4x - 8

Jatka samalla tavalla toiselle Integraatiovakio

f (x) = ∫f '(x) dx
∫ (4x - 8) dx = 2x² - 8x + c₂

Alkuolosuhde F (0) = 7 tunnetaan ja jatka:

2 (0)² - 8 (0) + C₂ = 7

C₂ = 7 ja f (x) = 2x² - 8x + 7

• f "(x) = x² ; f '(0) = 6; f (0) = 3

Samanlainen kuin edellisessä ongelmassa määrittelemme ensimmäiset johdannaiset ja alkuperäisen funktion alkuolosuhteista.

f '(x) = ∫f "(x) dx

∫ (x²) Dx = (x³/3) + c₁

Ehdolla f '(0) = 6 etenee:

Voi palvella sinua: Aseta teoria: Ominaisuudet, elementit, esimerkit, harjoitukset

(0³/3) + c₁ = 6; Missä₁ = 6 ja f '(x) = (x³/3) + 6

Sitten toinen Integraatiovakio

f (x) = ∫f '(x) dx

∫ [(x³/3) + 6] dx = (x⁴/12) + 6x + c₂

Alkuolosuhde F (0) = 3 tunnetaan ja jatka:

[(0)⁴/12] + 6 (0) + C₂ = 3; Missä₂ = 3

Erityinen primitiivinen saadaan

f (x) = (x⁴/12) + 6x + 3

Esimerkki 3

3. Määritä johdannaisten primitiiviset funktiot ja kuvaajan piste:

• dy/dx = 2x - 2, joka kulkee pisteen läpi (3, 2)

On tärkeää muistaa, että johdannaiset viittaavat käyrän tangentin kaltevuuteen tietyssä vaiheessa. Jos ei ole oikein olettaa, että johdannaisen grafiikka koskettaa osoitettua pistettä, koska se kuuluu primitiivisen funktion kaavioon.

Tällä tavalla ilmaisemme differentiaaliyhtälön seuraavasti:

dy = (2x - 2) dx  ; Sitten kun olet soveltanut antitointiperusteita, sinulla on:

∫Dy = ∫ (2x - 2) dx

y = x² - 2x + c

Alkuperäisen ehdon soveltaminen:

2 = (3)² - 2 (3) + C

C = -1

On saatu: f (x) = x² - 2x - 1

• dy/dx = 3x² - 1, joka kulkee pisteen läpi (0, 2)

Ilmaisemme differentiaaliyhtälön seuraavasti:

dy = (3x² - 1) DX  ; Sitten kun olet soveltanut antitointiperusteita, sinulla on:

 ∫Dy = ∫ (3x² - 1) DX

y = x³ - x + c

Alkuperäisen ehdon soveltaminen:

2 = (0)² - 2 (0) + C

C = 2

On saatu: f (x) = x³ - x + 2

Ehdotetut harjoitukset

Harjoitus 1

1. Löydä alkuolosuhteet vastaava primitiivinen F (x):

• f "(x) = x; f '(3) = 1; F (2) = 5
• f "(x) = x + 1; f '(2) = 2; f (0) = 1
• f "(x) = 1; f '(2) = 3; F (1) = 10
• f "(x) = -x; f '(5) = 1; f (1) = -8

Harjoitus 2

2. Ilmapallo, joka nousee 16 jalkaa/s.

• Määritä lentoaika
• Mikä on vektori v_F Kun kosketat lattiaa?

Harjoitus 3

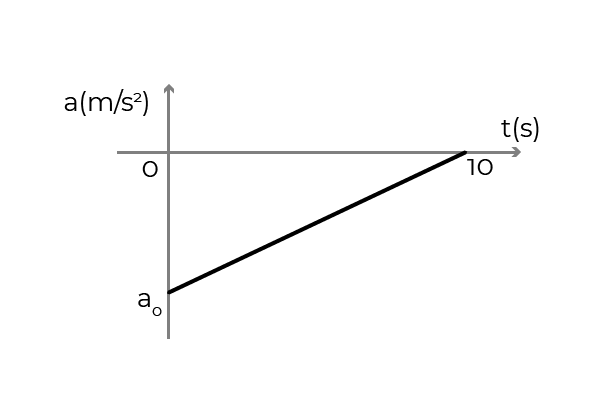
3. Kuvio näyttää kiihtyvyyskaavion - auton, joka liikkuu X -akselin positiivisessa merkityksessä. Auto matkusti vakiona 54 km/h, kun kuljettaja levitti jarrut pysähtyäkseen 10 sekunnissa. Päättää:

• Auton alkuperäinen kiihtyvyys
• Auton nopeus t = 5s
• Auton siirtyminen jarrutuksen aikana

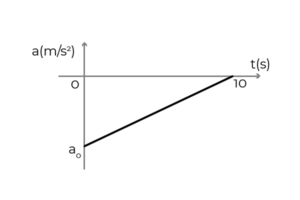Lähde: Kirjoittaja

Harjoitus 4

4. Määritä johdannaisten primitiiviset funktiot ja kuvaajan piste:

• dy/dx = x, joka kulkee pisteen läpi (-1, 4)
• dy/dx = -x² + 1, joka kulkee pisteen (0, 0) läpi
• dy/dx = -x + 1, joka kulkee pisteen läpi (-2, 2)

Viitteet

1. Kiinteä laskenta. Määrittelemättömät integraali- ja integraatiomenetelmät. Wilson, Velásquez Bastidas. Magdalena 2014 University
2. Stewart, J. (2001). Muuttujan laskenta. Varhainen transsendentti. Meksiko: Thomson Learning.
3. Jiménez, r. (2011). Matematiikka VI. Kiinteä laskenta. Meksiko: Pearson Education.
4. Fysiikka i. MC Graw Hill