Kriteerit samanlaiset kolmiot

Mitkä ovat kolmioiden samankaltaisuuskriteerit?

Kolmioiden samankaltaisuuskriteerit ovat säännöt, jotka sallivat tietää, ovatko kaksi kolmiota samanlaisia. Geometristen lukujen, mukaan lukien kolmiot, samankaltaisuus edellyttää, että luvuilla on samalla tavalla, vaikka niillä ei välttämättä ole saman kokoisia tai samaa suuntausta.

Kaksi kolmiota ovat samanlaisia, on välttämätöntä, että: i) heidän homologiset sivut ovat verrannollisia ja ii) kunkin sisäkulmalla on sama mitta.

Kuvio 1. Kaksi samanlaista kolmiota: Vaikka niillä ei ole samankokoisia, niiden sivut ovat verrannollisia ja niiden sisäiset kulmat ovat yhtä suuret. Lähde: f. Zapata.

Kahden määrän A ja B välinen suhteellinen suhde tai osuus edustaa A/B -suhde, b ≠ 0. Samankaltaisille kolmioille seuraavat niiden sivujen väliset mittasuhteet ovat päteviä:

a/a '= b/b' = c/c '= r

R -arvoa kutsutaan samankaltaisuus.

Lisäksi vastaavien sisäisten kulmien on oltava sama mitta, siksi: ∠A = ∠A '; ∠B = ∠B 'ja ∠C = ∠C'. Näiden olosuhteiden mukaan kolmioiden samankaltaisuuskriteerit ovat:

Kriteerit 1: Kaksi kolmiota ovat samanlaisia, jos niillä on kaksi yhtä suurta sisäkulmaa. Jos näin on, kolmas kulma mittaa myös saman, koska minkä tahansa kolmion sisäkulmien summa on 180º:

α = α '; β = β '

Kriteerit 2: Kolmiot ovat samanlaisia, jos kaksi homologista puolta ovat verrannollisia ja niiden välinen kulma on sama:

a/a '= b/b'; α = α '

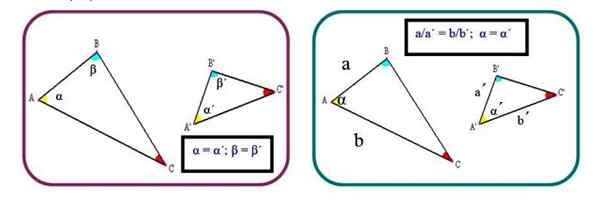Kuva 2. Kaksi kriteeriä kolmioiden samankaltaisuuden määrittämiseksi. Lähde: f. Zapata.

Kriteerit 3: Kolme homologista puolta ovat verrannollisia:

a/a '= b/b' = c/c '= r

Esimerkit

Kolmioiden samankaltaisuus on erittäin hyödyllinen korkeuksien ja etäisyyksien laskemisessa, joita ei voida helposti mitata suoraan. Joidenkin yksinkertaisten laskelmien avulla on mahdollista selvittää nämä pituudet vertaamalla samanlaisia ​​kolmioita.

Voi palvella sinua: Aritmeettisen peruslause: demonstraatio, sovellukset, harjoitukset

Pylväiden, rakennusten ja puiden korkeus

Sanotaan, että muinaisen Kreikan geometrian isä, kuten Miletus.C.), laski temppelin pylvään korkeus ilman erityisiä instrumentteja, vain vertaamalla sen sokeriruo'on varjopitoa pylvään pituuteen ja soveltamalla kolmioiden samankaltaisuutta. Samalla menetelmällä hän onnistui mittaamaan Egyptin suuren pyramidin korkeuden ja siten vaikuttamaan faaraoon.

Etäisyys kuuhun

Maan ja kuun välisen etäisyyden laskemiseksi on tehty yksinkertainen koe. Se vaatii valuutan, vähän liimanauhaa ja vernieriä tai jatko -sääntöä. Kun kuu on täynnä, valuutta kiinnitetään ikkunan lasiin ja kuu havaitaan yhdellä silmällä, joka sijaitsee siten, että valuutta kattaa vain täysikuun.

Kun tämä tapahtuu, syy valuutan halkaisijan ja silmän ja valuutan välisen etäisyyden välillä on sama, että kuun ja silmän ja kuun välisen etäisyyden välillä on sama:

Valuutan halkaisija/etäisyysvaluutta = kuun halkaisija/etäisyys kuuhun

Syynä on noin 1/110. Mikä tarkoittaa, että etäisyys kuuhun on 110 -kertainen tämän halkaisija.

Tällä hetkellä kuun säde arvioidaan vuonna 1737.1 km, joten sen halkaisija on 3474.2 km. Korvaamalla tämä arvo suhteessa:

Etäisyys kuuhun = kuun halkaisija ÷ (valuutan halkaisija/etäisyys valuuttaan)

On saatu:

Etäisyys kuuhun = 3474.2 km ÷ (1/110) = 382.162 km

Se voi palvella sinua: hepagonaalinen prisma

Hyvin lähellä 384 tähtitieteilijän määrittämää arvoa.000 km.

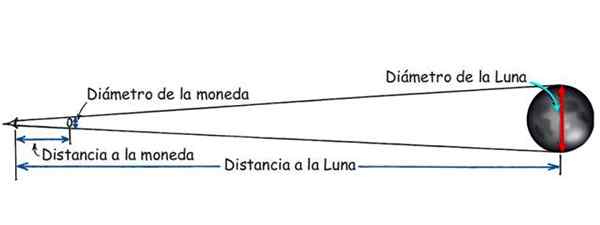Kuva 3. Etäisyys kuuhun voidaan tietää kolmioiden samankaltaisuuden ansiosta. Lähde: Muokattu Hewitt, P. Käsitteellinen fysiikka.

Etäisyys aluksen ja rannan välillä

Laivan ja rannan välisen etäisyyden mittaamiseksi panokset ovat juuttuneet rannalle pisteissä A, B, C ja Q. ABC- ja PCQ -kolmiot ovat samanlaisia ​​kriteereillä 1, koska niillä on kaksi yhtä suurta kulmaa: kaksi kulmaa ∠C = α, joita kärki ja kaksi suoraa kulmaa vastaavat 90º: ∠B = ∠Q.

Kahden tällä tavalla sijaitsevan kolmion sanotaan olevan Thales -asema Ja ne ovat aina samanlaisia. Kolmiot tunnistetaan Thales -asennossa yhteisen kulman ja vastakkaisten sivujen kanssa kyseisessä kulmassa ovat yhdensuuntaiset.

Seuraavassa osassa on numeeriset arvot.

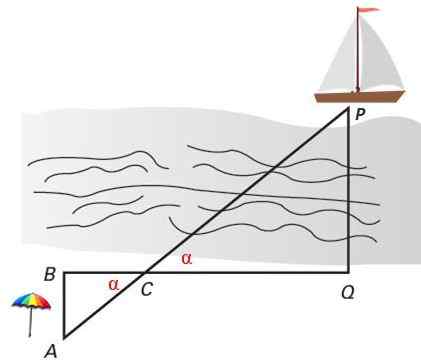Kuva 4. Kaksi samanlaista Thales -asennon kolmiota aikoo laskea laivan kohtisuoran etäisyyden rannalle. Lähde: f. Zapata.

Ratkaisut

Harjoitus 1

Haluat selvittää, kuinka pitkälle purjevene on ankkuroitu edelliseen hahmoon, pisteestä, joka sijaitsee rannan rannalla, jolle panokset naulataan pisteisiin A, B, C ja Q, määrittäen siten kolmion ABC, joka on samanlainen kuin PCQ, mutta joiden sivuja on helpompi mitata.

Laske kohtisuoran etäisyys PQ laivan ja rannan välillä kolmioiden samankaltaisuudella, jos käytettävissä olevat etäisyydet ovat:

AB = 12 m

BC = 16 m

QC = 60 m

Ratkaisu

Homologisten puolten väliset mittasuhteet ovat:

Ab/qp = bc/cq = 16 m/60 m = 0.267

Siksi 0.267 on syy samankaltaisuuteen:

Ab/qp = 0.267

Qp = ab / 0.267 = 12 m / 0.267 = 44.9 m

Harjoitus 2

Seuraavassa kolmiossa: kuinka paljon AD -segmentti mittaa?

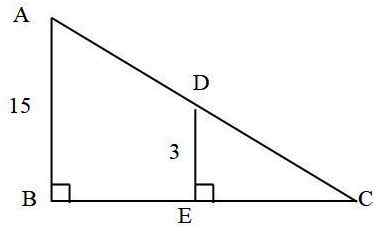
On tiedossa, että:

• AC = 25 cm
• AB = 15 cm
• De = 3 cm

Voi palvella sinua: 2: 2: MIKSI JA SELLITTELY

Ratkaisu

Kolmiot ovat samanlaisia, koska niillä on kulma, joka on ∠C ja sivut ja AB ovat yhdensuuntaiset. Samankaltaisuussuhde lasketaan:

R = AB / de = 15 cm / 3 cm = 5

Ja myös läpi:

R = AC / DC

Siksi DC = AC / R = 25 cm / 5 = 5 cm

Siitä asti kun:

AC = AD + DC

Tästä seuraa, että AD = AC - DC = 25 cm - 5 cm = 20 cm

Harjoitus 3

ISCELES -kolmion kehä on 49 cm ja pohja 21 cm. Laske tämän kaltaisen kolmion kehä, mutta jonka emäksen mitat ovat 4 cm.

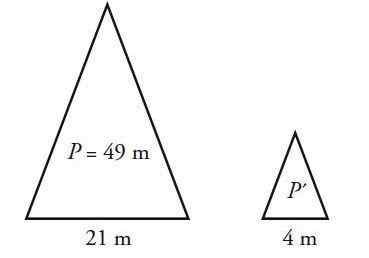
Ratkaisu

Iskosceles -kolmiossa on kaksi yhtä suurta sivua, erilainen kuin pohja B. Olkoon sivujen mitta ja p kehy, joka koostuu kolmen sivun summasta. Suurimmalle kolmiolle:

P = 2 ℓ + B = 49 cm

2 ℓ + 21 cm = 49 cm → ℓ = (49-21) cm / 2 = 14 cm

Nyt kolmioiden sivujen välinen osuus on nostettu, pienen kolmion osat symboloidaan vakuutusmaksuilla:

B/ b '= ℓ/ ℓ'

21 cm / 4cm = 14 cm / ℓ '→ ℓ' = 14 cm / (21 cm / 4cm) = 2.67 cm

Pienen kolmion kehä on:

P '= 2 ℓ' + b '= (2 x 2.67) cm + 4 cm = 9.33 cm.

Viitteet

1. Alexander, D. 2013. Geometria. Viides. Painos. Cengage -oppiminen.
2. Hewitt, Paul. 2012. Käsitteellinen fysiikka. Viides. Ed. Pearson.
3. Clemens, S. Geometria sovelluksilla. Addison Wesley.
4. Ibáñez, P. 2010. Matematiikka III. Cengage -oppiminen.
5. Jiménez, r. Matematiikka II: Geometria ja trigonometria. Toinen. Painos. Pearson.
6. Stewart, J. 2007. Ennakkoluulo. Viides. Painos. Cengage -oppiminen.
7. Viismat. Samos Aristarco: Aurinkojärjestelmän mitat. Palautettu: Vicmat.com