Nelikulmaiset elementit, ominaisuudet, luokittelu, esimerkit

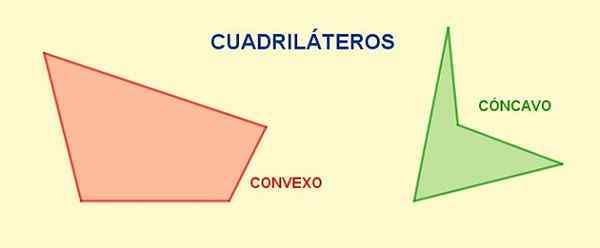
Eräs nelinkertainen Se on neljän puolen monikulmio ja neljä kärkipistettä. Heidän vastakkaiset puolet He ovat niitä, joilla ei ole yhteisiä kärkipisteitä, kun he ovat peräkkäiset puolet Ne, joilla on yhteinen kärki.

Neljänneksellä he ovat viereiset kulmat Ne, jotka jakavat sivun, vastakkaiset kulmat Heillä ei ole yhteisiä puolia. Toinen tärkeä ominaisuus kvadrilateraalille on, että sen neljän summa Sisäkulmat Se on kaksinkertainen tasainen kulma, eli 360º tai 2π radiaanit.

Kuvio 1. Erilaisia ​​nelikulmaisia. Lähde: f. Zapata.

Diagonaalit Ne ovat segmenttejä, jotka yhdistävät kärkipisteen vastakkaisella ja tietyssä renkaassa, jokaisesta kärkipisteestä voit piirtää yhden diagonaalin. Neljänneksen diagonaalien kokonaismäärä on kaksi.

Neljännekset ovat ihmiskunnalle tunnetut hahmot muinaisista ajoista lähtien. Arkeologiset tiedot sekä nykyään selviävät rakenteet todistavat sen.

Myös nykyään nelikulmaisilla on edelleen tärkeä läsnäolo kaikkien päivittäisessä elämässä. Lukija voi löytää tämän lomakkeen näytöltä, jolla teksti lukee tällä hetkellä, ikkunoissa, ovissa, autojen osissa ja lukemattomissa paikoissa.

[TOC]

Kvadrilateriaalien luokittelu

Vastakkaisten puolten rinnakkaisuuden mukaan nelikulmaiset luokitellaan seuraavasti:

1. Trapetsoidi, Kun rinnakkaisuutta ei ole ja nelikulmainen on kupera.
2. Trapetsi, Kun yhden vastakkaisen puolen parin välillä on rinnakkaisuus.
3. Suunnikas, Kun heidän vastakkaiset sivut ovat yhdensuuntaiset kaksi kahteen.

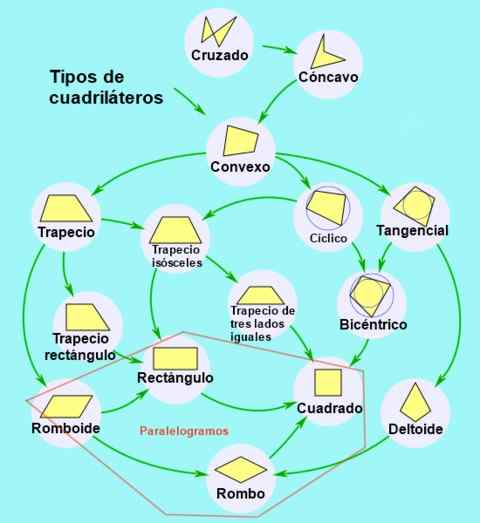Kuva 2. Kvadrilateriaalien luokittelu ja alaluokka. Lähde: Wikimedia Commons.

Rinnakkaistyypit

Rinnakkaisohjelmat puolestaan ​​voidaan luokitella niiden kulmien ja sivujen mukaan seuraavasti:

1. Suorakulmio, Juuri rinnakkaisgrammi on neljä sisäistä kulmaa, jotka ovat yhtä suuret. Suorakulmion sisäkulmat muodostavat suorakulman (90º).
2. Neliö, Se on suorakulmio, jonka neljä sivua on yhtä suuri.
3. Timantti, Se on rinnakkainen ohjelma neljän sivun kanssa, mutta sen erilaiset vierekkäiset kulmat.
4. Romboidi, rinnakkaisgrammi erilaisten vierekkäisten kulmien kanssa.

Trapetsi

Trapetsi on kupera kvadrilateraali, jolla on kaksi yhdensuuntaista sivua.

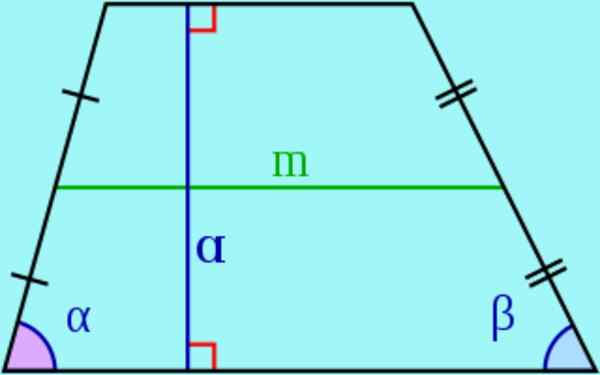Kuva 3. Trapetsin pohjat, sivuttaiset, korkeus ja mediaani. Lähde: Wikimedia Commons.

- Trapetsissa rinnakkaisia ​​sivuja kutsutaan pohjat Ja ei -paralleleja kutsutaan sivuttais-.

- Se korkeus trapetsista on kahden emäksen välinen etäisyys, ts. Segmentin pituus, jonka päät ovat emäksissä ja kohtisuorassa samaan. Tätä segmenttiä kutsutaan myös trapetsikorkeudeksi.

- Se mediaani Segmentti liittyy sivujen keskipisteisiin. Voidaan osoittaa, että mediaani on yhdensuuntainen trapetsin emäksien kanssa ja sen pituus on yhtä suuri kuin emäksen puolikehykset.

- Trapetsin pinta -ala on sen korkeus kerrottuna emäksen puolipisteillä:

Trapetsin pinta -ala = korkeus * (pohja 1 + pohja 2) / 2

Trapetsin tyypit

-Suorakaiteen trapetsi: Se on se, jolla on puoli kohtisuorassa pohjalta. Tämä puoli on myös trapezoidin korkeus.

-Trapezium -sammutus: Yksi, jolla on yhtä pitkä sivu. Akosceles trapezoidissa emäksen vieressä olevat kulmat ovat yhtä suuret.

-Escaleno trapezio: Se, jolla on eri pituus sivut. Sen vastakkaiset kulmat voivat olla akuutteja ja toinen tylsä, mutta voi myös tapahtua, että molemmat ovat tylsää tai molemmat akuutteja.

Voi palvella sinua: ratkaistu tekijäharjoitukset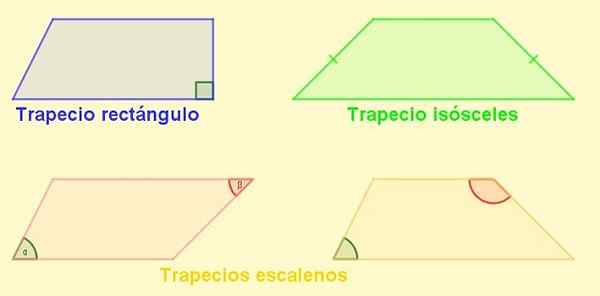 Kuva 4. Trapetsin tyypit. Lähde: f. Zapata.

Suunnikas

Parallelogrammi on kvadrilateraalinen, jonka vastakkaiset puolet ovat yhdensuuntaiset kaksi kahteen. Rinnakkaisogrammissa vastakkaiset kulmat ovat samat ja viereiset kulmat ovat täydentäviä tai toisin sanoen viereiset kulmat yhteensä 180º.

Jos rinnakkaisgrammilla on suorakulma, niin kaikki muut kulmat ovat myös ja tuloksena oleva luku kutsutaan suorakulmio. Mutta jos suorakulmion viereiset sivut ovat myös saman pituiset, niin kaikki sen sivut ovat yhtä suuret ja tuloksena oleva luku on neliö.

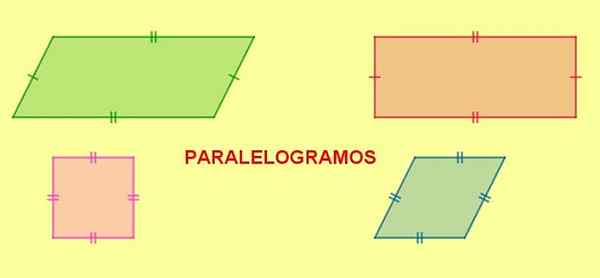Kuva 5. Rinnakkaisohjelmat. Suorakulmio, neliö ja rhombus ovat yhdensuuntaisia. Lähde: f. Zapata.

Kun rinnakkaisogrammilla on kaksi samanpituista vierekkäistä sivua, kaikki sen sivut ovat samanpituisia ja tuloksena oleva luku on timantti.

Rinnakkaisogrammin korkeus on segmentti, jonka päät ovat vastakkaisilla puolillaan ja kohtisuorassa niihin nähden.

Rinnakkaisohjelma

Rinnakkaisohjelman pinta -ala on pohjan tuote sen korkeudella, pohja on sivu, joka on kohtisuorassa korkeuteen (kuva 6).

Pinta -alan pinta -ala = pohja x korkeus = a . h

Rinnakkaisgrammin diagonaalit

Verteipistä alkavan diagonaalin neliö on yhtä suuri kuin mainitun kärkipisteen vieressä olevien molempien puolien neliöiden summa enemmän kyseisten sivujen kaksoistuote kyseisen kärjen kulman kosinusta:

F² = a² +  d -d² + 2 a d cos (α)

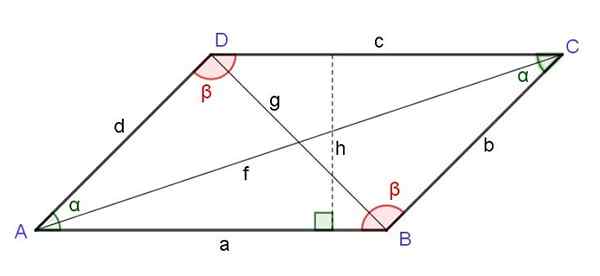Kuva 6. Suunnikas. Vastakkaiset kulmat, korkeus, diagonaalit. Lähde: f. Zapata.

Rinnakkaisogrammin kärkipaikkaan vastakkainen diagonaalin neliö on yhtä suuri kuin mainitun kärkipisteen vieressä olevien molempien sivujen neliöiden summa ja vähensi näiden sivujen kaksoistuotteen kyseisen kärjen kulman kosiinin avulla:

g² = a² + d -d² - 2 a d cos (α)

Rinnakkaisohjelma

Missä tahansa rinnakkaisohjelmassa niiden sivujen neliöiden summa on yhtä suuri kuin diagonaalien neliöiden summa:

-lla² + b -² + c² + d -d² = f² + g²

Keksinrypäle

Suorakulmio on nelikulmainen, jonka vastakkaiset puolet ovat yhdensuuntaiset kahdelle ja jolla on myös oikea kulma. Toisin sanoen suorakulmio on eräänlainen rinnakkainen ohjelma, jossa on oikea kulma. Rinnakkaisogrammille, Suorakulmion vastakkaiset sivut ovat yhtä pituisia a = c ja b = d. 

Mutta kuten missä tahansa viereisessä kulmassa olevassa rinnakkaisgrammissa ovat lisä- ja yhtäläisiä vastakkaisia ​​kulmia, suorakulmiossa on suorakulma, se muodostaa välttämättä suorat kulmat kolmeen muuhun kulmaan. Tarkoittaen Suorakulmiossa kaikki sisäkulmat mittaavat 90º tai π/2 radiaania.

Suorakulmion diagonaalit

Suorakulmassa diagonaalit ovat yhtä pituisia, Kuten alla esitetään. Perustelu on seuraava; Suorakulmio on yhdensuuntainen osittain suorakulmat ja siksi se perii kaikki rinnakkaisohjelman ominaisuudet, mukaan lukien kaava, joka antaa diagonaalien pituuden:

F² = a²+  d -d² + 2 a d cos (α)

g² = a² + d -d² - 2 a d cos (α)

kanssa α = 90º

Kuten Cos (90º) = 0, Joten tapahtuu, että:

F² = g² = a² +  d -d²

Tuo on f = g, ja siksi pituudet F ja g Suorakulmion kahdesta diagonaalista ne ovat yhtä suuret ja niiden pituus annetaan:

Suorakulmion diagonaalipituus = √ (a² + b -²-A

Lisäksi, jos vierekkäisten sivujen suorakulmio -lla ja b - Toinen puoli perustuu toiselle puolelle on korkeus, ja siten suorakulmioalue on:

Se voi palvella sinua: Fibonacci -sarja: Ominaisuudet, luonnolliset suhteet, sovellukset

Suorakulmion alue = a x b.

Ympäristö on suorakulmion kaikkien puolten summa, mutta koska vastakohdat ovat samat, se on sitten tarpeen sivuille suorakulmiolle -lla ja b - Käymä annetaan seuraavalla kaavalla:

Suorakulmion kehä = 2 (a + b)

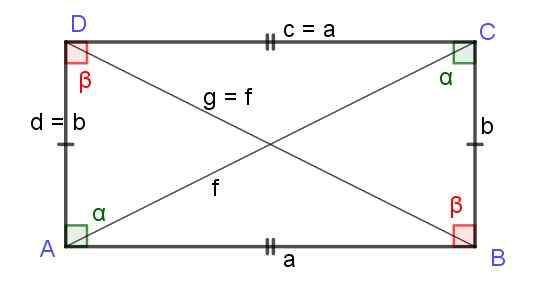Kuva 7. Sivujen a ja b suorakulmio. Diagonaalit f ja g ovat yhtä pituisia. Lähde: f. Zapata.

Neliö

Neliö on suorakulmio, jonka vierekkäiset sivut ovat saman pituiset. Jos neliöllä on puoli -lla, Sitten hänen diagonaalinsa F ja g Heillä on sama pituus, mikä on F = g = (√2) a.

Neliön pinta -ala on neliöön nostettu sivu:

Neliön pinta -ala = a²

Neliön kehä on kaksi kertaa puolella:

Neliön kehä = 4 a

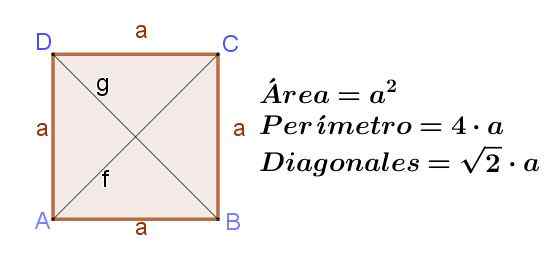Kuva 8. Neliö toiseen, mikä osoittaa sen pinta -alan, sen kehän ja sen diagonaalien pituuden. Lähde: f. Zapata ..

Timantti

Rhombus on yhdensuuntainen ohjelma, jonka vierekkäiset sivut ovat saman pituisia, mutta kuten yhdensuuntainen ollessa vastakkaiset sivut ovat samat, Rhombuksen kaikki puolet ovat yhtä pituisia.

Rhombuksen diagonaalit ovat eripituisia, mutta ne leikataan suorassa kulmassa.

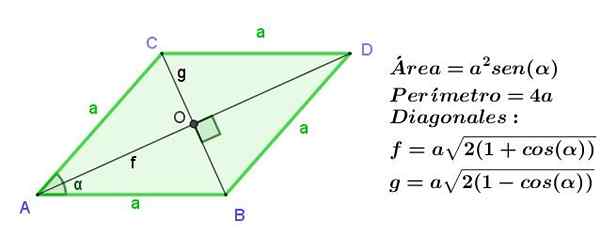Kuva 9. Rhombus sivulta A, mikä osoittaa sen pinta -alan, kehän ja sen diagonaalien pituuden. Lähde: f. Zapata.

Esimerkit

Esimerkki 1

Osoita, että nelikulmiossa (ei ylitetty) sisäkulmat yhteensä 360º.

Kuva 10: Se osoitetaan neljänneksen kulmien summana 360º. Lähde: f. Zapata.

ABCD: tä pidetään ABCD: nä (katso kuva 10) ja diagonaalinen BD piirretään. Muodostuu kaksi ABD- ja BCD -kolmiota. ABD -kolmion sisäkulmien summa on:

α + β₁ + Δ₁ = 180º

Ja BCD -kolmion sisäkulmien summa on:

 β2 + y + δ₂ = 180º

Kahden yhtälön lisääminen saadaan:

α + β₁ + Δ₁ +  β₂ + γ + δ₂ = 180º + 180º

Ryhmittely:

α + (β₁ +  β₂) + (Δ₁ + Δ₂) + γ = 2* 180º

Ryhmittely ja uudistaminen, on vihdoin osoitettu, että:

α + β + Δ + γ = 360º

Esimerkki 2

Osoita, että trapetsoidin mediaani on samansuuntainen sen emäksen kanssa ja sen pituus on emäksen puolivälissä.

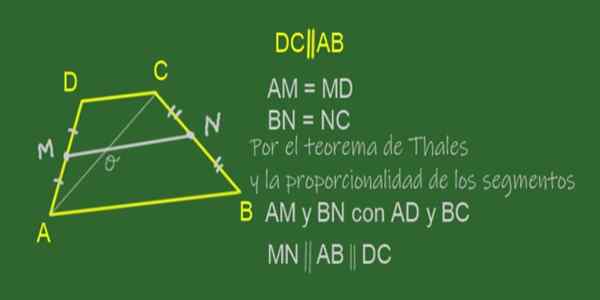Kuva 11. ABCD -trapetsin mediaani MN. Lähde: f. Zapata.

Trapetsin mediaani on segmentti, joka liittyy sivujensa keskipisteisiin, toisin sanoen ei -rinnakkaiset puolet. Kuvassa 11 esitetyssä ABCD -trapetsissa mediaani on Mn. 

Koska se on AD: n ja N: n puolivälissä BC -pisteen keskipiste, on täytettävä, että jako AM / AD ja BN / BC ovat yhtä suuret.

Toisin sanoen AM on verrannollinen BN: hen samassa suhteessa kuin AD on BC, joten Thalesin lauseen (vastavuoroinen) soveltamisolosuhteet seuraavat:

"Jos kolmella tai useammalla suorassa leikkauksessa kaksi sekuntia".

Meidän tapauksessamme päätellään, että MN-, AB- ja DC -viivat ovat siksi yhdensuuntaisia,: siksi:

"LYksi trapetsista on mediaanissa yhdensuuntainen sen emäksen kanssa".

Voi palvella sinua: yhdistetyt toiminnot

Nyt Thalesin lause sovelletaan:

"Kahden tai useamman kuivumisen leikkausjoukko, joka on leikattu, määrää suhteelliset segmentit".

Tapauksessamme AD = 2 AM, AC = 2 AO, joten DAC -kolmio on samanlainen kuin MAO -kolmio ja siten DC = 2 kuukautta.

Samanlainen argumentti antaa vakuuttaa, että Cu on samanlainen kuin CON, missä CA = 2 CO ja CB = 2 CN. Tästä seuraa, että AB = 2 on.

Lyhyesti sanottuna, AB = 2 y 2 kuukaudessa. Joten kun olemme lähteneet:

AB + DC = 2 on + 2 mo = 2 (mo + on) = 2 mn

Lopuksi puhdistaa Mn:

Mn = (AB + DC) /2

Ja päätellään, että trapetsoidin mediaani mittaa emäksen puolijohtoja tai toisin sanoen: mediaani mittaa emäksen summan, jaettuna kahdella.

Esimerkki 3

Osoita, että rhombuksessa diagonaalit leikataan suorassa kulmassa.

Kuva 12. Rhombus ja esittely, että niiden diagonaalit leikataan suorassa kulmassa. Lähde: f. Zapata.

Kuvion 12 hallitus näyttää tarvittavan rakenteen. Ensinnäkin ABCD -rinnakkaisgrammi piirretään AB = BC: n kanssa, eli rhombus. AC- ja DB -diagonaalit määrittävät kuviossa kahdeksan kulmaa.

Lauseen käyttäminen (a.Yllyttää.p.) toteaa, että SECANT: n katkaisemien rinnakkaisten väliset sisäiset vaihtoehtoiset kulmat määrittävät yhtäläiset kulmat, voimme määrittää seuraavat:

α₁ = γ₁, α2 = y2, δ₁ = Β₁ ja Δ2 = β2. (*)

Toisaalta, koska rhombuksen vierekkäiset sivut ovat yhtä pituisia, määritetään neljä tasapainoista kolmiota:

DAB, BCD, CDA ja ABC

Nyt vedotaan kolmiolausekkeeseen (samaskles), jonka mukaan pohjan vieressä olevat kulmat ovat yhtä suuret, missä päätellään:

Δ₁ = β2, Δ2 = β₁, α2 = y₁ ja α₁ = γ2 (**)

Jos suhteet (*) ja (**) yhdistetään, seuraavat kulmien tasa -arvot:

α₁ = α2 = γ₁ = γ₁ Toisaalta ja β₁ = Β2 = δ₁ = Δ2 toiselle. 

Muistaminen tasavertaisten kolmioiden lauseen muistaminen, jotka vakuuttavat, että kaksi kolmiota, joilla on yhtä suuri puoli kahden yhtä suuren kulman välillä, ovat samat:

Aod = aob ja siten myös kulmat ∡aod = ∡aob.

Sitten ∡Aod + ∡AoB = 180º, mutta koska molemmat kulmat ovat yhtä suuret, 2 ∡Aod = 180º, mikä tarkoittaa, että ∡Aod = 90º.

Toisin sanoen geometrisesti osoitetaan, että rhombuksen diagonaalit leikataan suorassa kulmassa.

Ratkaistu harjoitus

- Harjoitus 1

Osoita, että suorakulmiossa trapezoidissa ei-EG-kulmat ovat lisä.

Ratkaisu

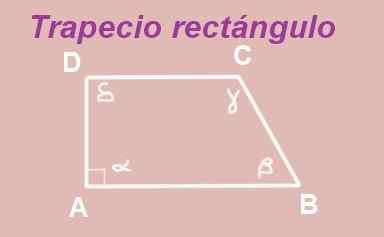Kuva 13. Suorakaiteen trapetsi. Lähde: f. Zapata.

ABCD Trapezoid on rakennettu rinnakkaisilla AB- ja DC -emäksillä. Vertex A: n sisäkulma on suora (mittaa 90º), joten sinulla on suorakulmio trapezoidi.

Kulmat α ja δ ovat sisäkulmat kahden rinnakkaisen AB: n ja DC. 

Toisaalta on osoitettu, että nelikulmaisen sisäkulmien summa lisää 360º, ts

α + β + γ + Δ = 90º + β + 90º + Δ = 360º.

Yllä oleva johtaa:

 β + Δ = 180º

Vahvistetaan, mitä halusi osoittaa, että kulmat β ja δ ovat täydentäviä.

- Harjoitus 2

ABCD: n rinnakkaisgrammilla on AB = 2 cm ja AD = 1 cm, lisäksi kulma huono on 30º. Määritä mainitun rinnakkaisogrammin ja sen kahden diagonaalin pituus.

Ratkaisu

Rinnakkaisohjelman pinta -ala on sen pohjan pituuden tuote korkeuden mukaan. Tässä tapauksessa segmentin B = AB = 2 cm pituus otetaan pohjana, toisella puolella on pituus A = AD = 1 cm ja korkeus H lasketaan seuraavasti:

H = AD * sin (30º) = 1 cm * (1/2) = ½ cm.

Sitten: Alue = B * H = 2 cm * ½ cm = 1 cm².

Viitteet

1. C. JA. -Lla. (2003). Geometriaelementit: harjoituksilla ja kompassin geometrialla. Medellinin yliopisto.
2. Campos, f., Cerecedo, f. J -. (2014). Matematiikka 2. Patria -toimitusryhmä.
3. Vapautettu, k. (2007). Tutustu monikulmioihin. Vertailuindeksiyhtiö.
4. Hendrik, V. (2013). Yleiset monikulmiot. Birkhäuser.
5. Iger. (S.F.-A. Matematiikka ensimmäisen lukukauden Tacaná. Iger.
6. Jr. Geometria. (2014). Monikulmio. Lulu Press, Inc.
7. Miller, Heeren ja Hornsby. (2006). Matematiikka: Perustelu ja sovellukset (kymmenes painos). Pearson -koulutus.
8. Patiño, m. (2006). Matematiikka 5. Toimitusohjelma.
9. Wikipedia. Nelinkertainen. Palautettu: on.Wikipedia.com