Jäykkä runko

Mikä on jäykkä ruumis?

Jäykkä runko on materiaalinen esine, jonka hiukkaset pysyvät aina samoissa suhteellisissa paikoissa. Siksi se on objekti, jota ei ole muodonmuutos, laatu, joka on annettu voimakkaille koheesiovoimille, jotka pitävät hiukkaset paikoillaan.

Itse asiassa minkä tahansa ulkoisten voimien alaisten kehon hiukkaset yleensä värähtelevät tai liikkuvat, joten esine on aina jossain määrin muodonmuutos, mutta nämä vaikutukset ovat yleensä pieniä.

Kun näin on, voidaan olettaa, että vartalo on jäykkä ja sillä on erittäin hyvä lähestymistapa sen käyttäytymiseen, vaikka se olisi idealisointi.

Jäykät rungottyypit

Voit erottaa kahden tyyppisen jäykän rungon:

• Ne, joiden hiukkaset ovat erillisiä määriä, eli ne voivat laskea. Esimerkiksi kahta metallipalloa, jotka on kytketty ohuella ja kevyellä sauvalla, voidaan pitää ainutlaatuisena kokonaisuutena. Jos sauva on tarpeeksi jäykkä olla taipumatta, järjestelmää pidetään jäykänä rungona.
• Ne, jotka ovat jatkuvia, mikä tarkoittaa, että ne tekevät hiukkaset ovat erottamattomia. Jokapäiväinen ja luonto -esineet ovat hyviä esimerkkejä: kivet, huonekalut ja muut, samoin kuin maa ja muut taivaalliset kivet kiviset.

Jäykkä kehon liike ja dynamiikka

Kuten hiukkasina pidetyt esineet, jäykät kappaleet voidaan siirtää, kiertää ja niillä on yleisempi liike, yhdistämällä käännös ja kierto.

Käännöksen tutkimiseksi se ei ole välttämätöntä.

Nämä käännös- ja kiertoliikkeet voivat olla:

• Itsenäinen, kuten planeettojen tapauksessa, joiden kiertoliike on heidän akselinsa (pidetään kiinteänä) ja toinen käännös auringon ympärillä, mutta kunkin nopeudet eivät ole yhteydessä toisiinsa.
• Rikkoutunut roskaa, jos massakeskuksen kulmanopeus ja käännösnopeus liittyvät. Tässä tapauksessa kierto -akseli on liikkuvaa, kuten sylinterin tapauksessa, joka menee alaspäin liukumatta kaltevalla kaltevuudella.

Se voi palvella sinua: Termodynamiikan ensimmäinen laki: kaavat, yhtälöt, esimerkit

Jäykän kiinteän kiinteän aineen dynamiikka

Seuraavat suuruudet ovat merkityksellisiä jäykän kiinteän aineen dynamiikassa:

Massakeskus

Massan keskipiste on kohta, jossa koko kehon massa katsotaan olevan keskittynyt. Jos se on homogeeninen ja symmetrinen runko, pallona, ​​massan keskipiste tapahtuu samanaikaisesti geometrisen keskuksen kanssa.

Hitaushetki

Tämä skalaarinen suuruus on kiertohitauden tai vastusarvo, joka vastustaa kohdetta kiertämään tietyn akselin ympäri. Se riippuu täysin esineen geometriasta ja sen massasta, ja siksi tietyissä tapauksissa on helpompaa kääntää tiettyjä akseleita kuin toiset.

Runkoille, joilla on hyvin määriteltyjä geometrisia muotoja, on taulukoita, joissa on hitausmomentteja symmetrian akselien suhteen, esimerkiksi se, joka kulkee massan keskuksen läpi. Näiden tietojen ja hitausmomenttiin liittyvien lauseiden avulla momentit muihin akseleihin voidaan helposti laskea.

Voimat ja vääntömomentti tai vääntömomentti

Voimat vaaditaan liikuttamaan ruumiin. Jos jäykkä kiinteä massakeskus liikkuu, liikeyhtälö Newtonin toisen lain mukaan: on:

F_Netto = M ∙-lla_cm

Missä:

-Nettovoima on F_Netto

-M on massa

-Massikeskuksen kiihtyvyys on -lla_cm

Kaikki sovelletut voimat eivät kuitenkaan tee esineiden rikkoutumista. Tätä varten tarvitaan vääntömomentti tai vääntömomentti, jossa sanotaan kuinka tehokas se on voiman pyörimisvaikutus. Se määritellään vektorituotteeksi sijaintivektorin välillä r - Tietyn pisteen ja voiman suhteen F kysymyksessä. Sitä merkitään kreikkalaisella kirjeellä τ (Lihavoidussa kirjeessä se on myös vektori):

Voi palvella sinua: elliptinen liike

τ = r - × F

Kansainvälisessä järjestelmässä vääntömomenttiyksikkö on N⋅m (Newton / metri).

Monissa tapauksissa pyörimisliike akselin ympärillä, joka kulkee massan keskuksen läpi, kuvataan vastaavalla yhtälöllä Newtonin toiseen lakiin:

Missä alaindeksi "Z" viittaa kierto -akseliin, joka kulkee symmetria -akselin läpi, kiinnitetty tai liikkuu, mutta muuttamatta suuntaa ja_cm Se on hitausmomentti massan ja a -keskuksen suhteen_{z -z} Se on kehon kulmakiihtyvyys. Kesä kattaa kaikki ulkoiset hetket Z -akselin ympärillä.

Jäykän kiinteän aineen kineettinen energia

Jäykän rungon liikettä kuvataan massa- ja kiertokeskuksen käännöksillä sen pisteen ympärillä, siksi sen kineettinen energialla on molemmat vaikutukset.

Olkoon k kehon kineettinen energia, v_cm Massikeskuksen nopeus, m: n kehon massa ja_cm sen hitausmomentti massakeskuksen ja ω kulmanopeuden suhteen. Voidaan osoittaa, että kineettinen energia on:

K = ½ mV_cm² + ½ i_cm Ω²

Havaitaan, että toinen oikealla oleva termi on vasemman termin pyörimisanalogi. Siellä hitausmomentti on sama rooli kuin massalla, kun taas kulmanopeudella on sama rooli kuin lineaarisella nopeudella.

Esimerkkejä jokapäiväisessä elämässä

Fyysinen heiluri

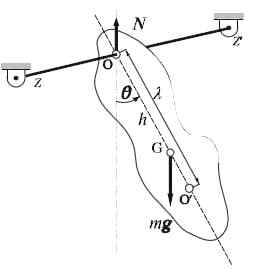Fyysinen heiluri

Fyysinen heiluri tai todellinen heiluri on erittäin helppo rakentaa: se koostuu jäykästä kiinteästä, kuten sauva tai tanko, värähtelemällä vapaasti vaakasuoran akselin ympärillä. Kierto -akseli ei ylitä esineen massan keskipistettä, ja tällä periaatteessa voi olla minkä tahansa muodon.

Voi palvella sinua: Resistanssilämpömittari: Ominaisuudet, toiminta, käyttö

Tämä heiluri eroaa yksinkertaisesta heilurista, koska jälkimmäisessä katsotaan, että sen säveltämä massa on täsmällinen.

Pyöräpyörä

Pyöräpyörä

Toinen hyvin tunnettu jäykkä runko -esimerkki on polkupyöräpyörä, jonka akseli kulkee massakeskuksen läpi, joka ylittää pyörän keskustan. Niin kauan kuin ne eivät nojaa sivulle tai kääntymään, kuvattujen dynamiikan yhtälöt sovelletaan liikkeen kuvaamiseen.

Keilapallo

Hyvä esimerkki jäykästä ruumiista on keilapallo

Jäykkä kiinteä malli mukautuu erittäin hyvin kuvaamaan keilapallon liikettä radalla tai kun se rullaa liu'uttamatta paluumatkaa alaspäin.

Yoyo

Yoyo on suosittu lelu, joka voidaan mallintaa kuin jäykkä runko

Tämä suosittu lelu on valmistettu puu- tai muovisylinteristä ja köydestä, joka on hätkähdyttävä sitä ympäröivään paikkaan.

Sylinteri voidaan mallintaa jäykkänä rungona, jossa merkkijonon jännite tarjoaa kiertoa koskevan vääntömomentin, kun taas paino (sovellettu massan keskustaan) ja jännitys on vastuussa massan keskuksen pystysuuntaisesta kiihtyvyydestä.

Viitteet

1. Bauer, W. 2011. Fysiikka tekniikkaan ja tieteisiin. Osa 1. MC Graw Hill. 
2. Giancoli, D.  2006. Fysiikka: sovellusten periaatteet. Kuudes. Ed Prentice Hall.
3.  Katz, D. 2013. Fysiikka tutkijoille ja insinööreille. Perusteet ja yhteydet. Cengage -oppiminen.
4. Sears, Zemansky. 2016. Yliopiston fysiikka, jolla on moderni fysiikka. 14. päivä. Ed. Osa 1. Pearson.
5. Serway, R., Jewett, J. (2008). Fysiikka tieteen ja tekniikan fysiikka. Osa 1. Seitsemäs. Ed. Cengage -oppiminen.