Kuinka monta halkaisijaa kehällä on?

Ympäristöllä on ääretön halkaisija. On helppo nähdä, että se on niin, jos se perustuu halkaisijan määritelmään, joka on segmentti, joka kulkee samanaikaisesti ympäryskeskuksen läpi ja kahdella pisteellä.

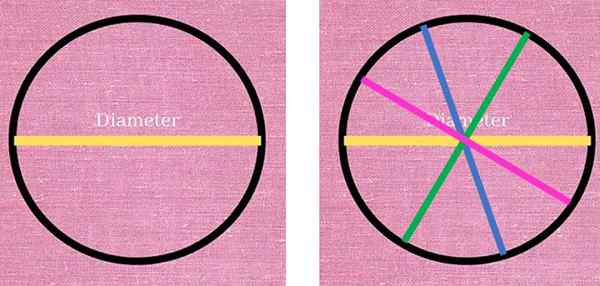
Seuraavassa kuvassa vasemmalla, kehän halkaisijaa vastaava keltainen viiva havaitaan ja jaetaan kahteen osaan. Oikealla puolella kolme muuta halkaisijaa piirrettiin eri väreissä: sininen, vihreä ja vaaleanpunainen. Kaikilla on sama pituus ja ne täyttävät kehän kahden pisteen yhdistämisen ehto saman keskuksen läpi.

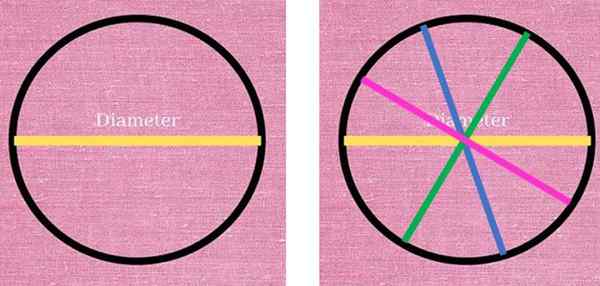Halkaisija on erottuva segmentti, joka kulkee aina ympärysmiipan keskustan läpi ja yhdistää tämän kaksi pistettä. Vasemmalla puolella keltainen halkaisija jakaa kehän kahteen. Oikealla on myös muita halkaisijoita, jotka myös jakavat kehän kahteen puolikkaaseen. Lähde: f. Zapata.

Kuten voidaan nähdä, halkaisijoiden piirtämismahdollisuudet ovat loputtomia, koska äärettömät ovat kohtia, jotka muodostavat ympärysmiipan. Sama voidaan vahvistaa säteen suhteen, joka on segmentti, joka yhdistää minkä tahansa kehän pisteen keskuksen kanssa: Radioiden ääretön määrä voidaan piirtää.

Ja kun asetat kaksi vastakkaista radiota toisistaan, saadaan halkaisija, koska säde mittaa puolet tästä.

Halkaisija, radio- ja kehän pituus

Olipa se minkä tahansa kehän ja r, sen säde. Koska halkaisija mittaa kaksi kertaa niin paljon kuin radio, se voidaan kirjoittaa:

D = 2 ∙ r

Se tarkoittaa, että jos ympyrän säde on esimerkiksi r = 5 cm, sen halkaisija on d = 2 ∙ 5 cm = 10 cm.

Se voi palvella sinua: Fibonacci -sarja: Ominaisuudet, luonnolliset suhteet, sovellukset

Halkaisija tunnetaan myös nimellä Pääke. Jouset ovat viivoja tai segmenttejä, jotka on piirretty kehän kahden pisteen väliin, mutta jotka eivät välttämättä kulkea keskuksen läpi. Vain halkaisijalla on tämä ero.

Seuraavassa kuvassa voit nähdä eron ja nähdä, miksi halkaisija (punainen) on suurimpi jousista, jotka voidaan piirtää kehään:

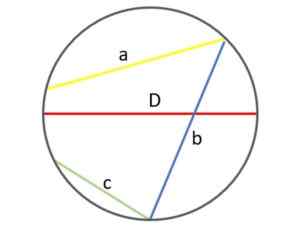Erilaiset köysit kehässä: halkaisija on suurin kaikista. Lähde: f. Zapata.

Tietenkin halkaisijan mitta (ja siksi säde) on sama tietyssä kehässä. Kun vaihtelee, saadaan pienempi tai suurempi ympärysmitta.

Toisaalta saman kehän jousien koko vaihtelee riippuen siitä, kuinka pitkälle tai lähelle pisteitä ovat kohdat, jotka liittyvät. Esitetyssä esimerkissä vihreä “C” -köysi on näennäisesti lyhyempi kuin “A” ja “B” -jonot.

Ja myös piirrettävien merkkijonojen lukumäärä on myös ääretön.

Kehän kehä

Ympyrän pituus puolestaan ​​vastaa sen kehää tai muotoa. Se liittyy halkaisijaan, koska mitä korkeampi tämä, sitä suurempi kehä (sen kehä on suurempi).

Kehyn ja halkaisijan välinen suhde tai osuus on vakio nimeltään π (lukee "PI"). Π -arvo on 3.141592… Suspensiot osoittavat, että desimaalien ja äärettömän määrä, mikä johtuu siitä, että PI on irrationaalinen luku. Käytännössä PI voi kuitenkin yksinkertaisesti pyöristää 3.14

Voi palvella sinua: kuinka paljon sinun on lisättävä 3/4 saadaksesi 6/7?

Jos kehä on merkitty C: ksi ja halkaisija D: ksi, tämä syy nostetaan seuraavasti:

C / d = π

Siksi kehän pituuden kaava on:

C = π ∙ d

Tai jos se on suositeltavaa säteen R: n perusteella:

C = 2π ∙ r

Havainnollistava esimerkki

Kuvassa on kolme identtistä kehää, jotka on nimetty kirjaimilla A, B ja C. Jokaisessa muurahainen kulkee tietä sinisellä värisegmenteillä, siirtyäkseen ympäryskohdasta toiseen.

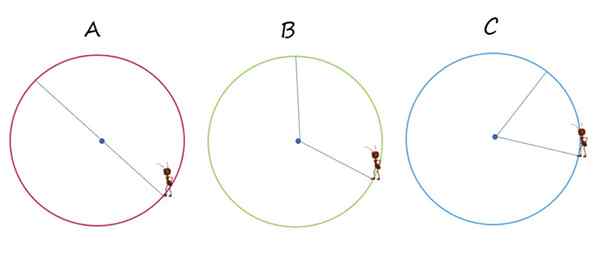ANT siirtyy pistemäärästä toiseen kehästä ohuimpien sinisten viivojen läpi. Lähde: f. Zapata.

1.- Missä tapauksissa siirtymä tapahtuu tarkalleen kehän halkaisijalla?

Vastaus

Vain tapauksessa A, koska tämä polku kulkee kehän keskustan läpi ja menee pisteestä toiseen samasta.

2.- Kuinka monta radiota hyönteinen kulkee kussakin tapauksessa?

Vastaus

Missä tahansa kolmesta tapauksesta muurahainen kulkee kaksi kehän radiota.

3.- Mikä polkuista vastaa suurinta etäisyyttä?

Vastaus

Matka on kussakin tapauksessa yhtä pitkä, mikä vastaa kehän kahta radiota.

4.- Jolloin muurahainen on kauempana lähtökohdastaan?

Vastaus

Tapauksessa A, koska juuri sen edessä on juuri sen edessä, muurahainen on lähempänä lähtökohtaa.

5.- Ja tällöin muurahainen päättyy reitti lähempänä lähtökohtaa?

Voi palvella sinua: ryhmittelyn merkkejä

Vastaus

Tapauksessa c.

6.- Jos kehän säde on 20 cm, kuinka monta senttimetriä kukin reitti mittaa?

Vastaus

Koska muurahainen kulkee etäisyys, joka on yhtä suuri kuin kaksi radiota, kulkenut kokonaismatka on 40 cm.

Ratkaisut

Harjoitus 1

Laske ympyrän säde, jonka halkaisija on 4.5m.

Ratkaisu

Radio on puolet halkaisijasta, jos tämä mittaa 4.5 cm, sitten radio r on 2.25 cm.

Harjoitus 2

Löydä harjoituksen 1 ympärysmittari.

Ratkaisu

Kehä lasketaan halkaisijan läpi tai säteen läpi, kuten suositeltavaa. Ensimmäisessä tapauksessa:

C = π ∙ d

Olettaen, että π = 3.14 Kierrokseen arvojen korvaaminen antaa seuraavan tuloksen:

C = π ∙ d = 3.14 ∙ 4.5 cm = 14.13 cm

Harjoitus 3

Suunnittelijaa pyydetään piirtämään sydämen muotoinen logo, ja kuvassa on merkitty mitat. Kaarevat osat vastaavat tarkkoja puolipirkuja.

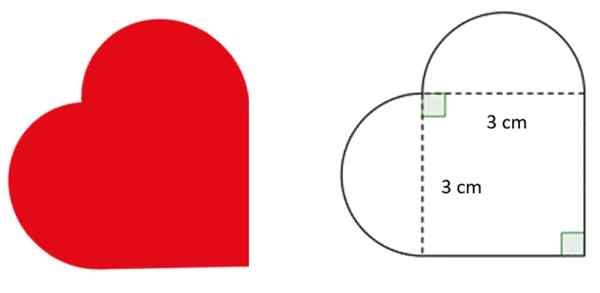
Näiden tietojen kanssa: Vastaus:

1. Mikä on puolipisteen säde?
2. Kuinka paljon sydämen kehä on?

Liittää jhk

Puolipirkujen halkaisija vastaa neliön sivua, joka on 3 cm. Siksi sen säde, joka on puoli, mittaa 1.5 cm.

Ratkaisu b

Sydämen muotoisen kuvan kehä on neliön kahden ulkopuolen ja puolivaltion kehän summa. Kuten identtinen, sen kehä on yhtä suuri kuin halkaisija 3 cm: n kokonaispiiri:

C = π ∙ d = 3.14 ∙ 3 cm = 9.42 cm

Siksi kuvan kehä P on:

P = 9.42 cm + 3 cm + 3 cm = 15.42 cm