CurtoS -määritelmä, tyypit, kaavat, mihin se on esimerkiksi

Se Kurtoosi tai kurtoosi Se on tilastollinen parametri, joka auttaa karakterisoimaan satunnaismuuttujan todennäköisyysjakaumaa, mikä osoittaa arvojen pitoisuuden asteen keskusmittauksen ympärillä. Tämä tunnetaan myös nimellä "huippulaatu".

Termi tulee kreikkalaisesta "kurtos", joka tarkoittaa kaarevaa, siksi roskosta osoittaa jakauman osoitus- tai tasoitusasteen, kuten seuraavassa kuvassa havaitaan:

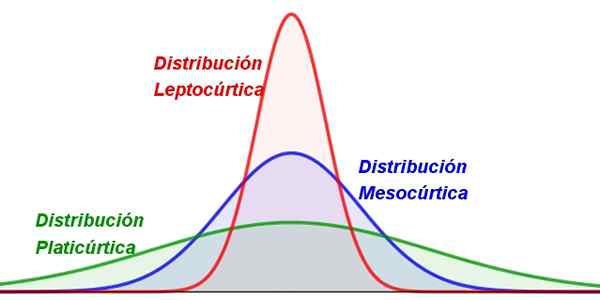Kuvio 1. Erityyppiset Turosis. Lähde: f. Zapata.

Lähes kaikki satunnaismuuttujan arvot pyrkivät ryhmittelemään keskiarvon, kuten keskiarvo. Mutta joissain jakautumisissa arvot ovat hajaantuneempia kuin toisissa, mikä johtaa litistetyihin tai hoikkaampiin käyriin.

[TOC]

Määritelmä

Curtosis on kunkin taajuusjakauman numeerinen arvo, joka arvojen pitoisuuden mukaan keskiarvon ympärillä luokitellaan kolmeen ryhmään:

-Leptocuric: jossa arvot on ryhmitelty hyvin keskiarvon ympärille, joten jakauma on melko terävä ja hoikka (kuva 1, vasen).

-Mesocurinen: Sillä on kohtalainen arvopitoisuus keskimäärin (kuva 1 keskellä).

-Fylicurinen: Tällä jakaumalla on laajempi muoto, koska arvot ovat yleensä hajallaan (kuva 1 oikealle).

Kaavat ja yhtälöt

Curtorylla voi olla mitään arvoa ilman rajoituksia. Sen laskelma suoritetaan tietojen toimittamisesta riippuen. Kummassakin tapauksessa käytetty merkintä on seuraava:

-Kortoosikerroin: g₂

-Aritmeettinen keskiarvo: X tai x baarilla

-I-ENE: x_Yllyttää

-Vakiopoikkeama: σ

-Tietojen lukumäärä: N

-I-ESIMO: n taajuus: F_Yllyttää

-Luokan tuotemerkki: mx_Yllyttää

Tämän merkinnän avulla esittelemme joitain yleisimmin käytettyjä kaavoja Curtory:

Voi palvella sinua: vektoritila: pohja ja mitta, aksioomit, ominaisuudet

- Kostoosi tietojen esittämisen mukaan

Ryhmittelemättä tai ryhmittelemättä tietoja taajuuksilla

Tiedot, jotka on ryhmitelty väliajoin

Ylimääräinen roski

Kutsutaan myös Fisherin osoituskerroin jompikumpi Fisher -mitta, Sen tarkoituksena on verrata tutkittavan jakauman jakautumista normaaliin jakautumiseen.

Kun ylimääräinen rostos on arvon arvoinen, olemme normaalin jakautumisen tai Gauss Bellin läsnäollessa. Tällä tavalla, niin kauan kuin jakauman ylimääräinen parkitus lasketaan, vertaamme sitä normaaliin jakaumaan.

Sekä tietojen osalta ryhmittelemättä että ryhmiteltyihin tietoihin kalastajan osoittamiskerroin, jonka merkitsee K, on:

K = g₂ - 3

Voidaan kuitenkin osoittaa, että normaalin jakautumisen rosto on 3, siksi, jos Fisherin osoituskerroin on 0 tai lähellä 0 ja mesocurinen jakauma on. Jos k> 0, jakauma on leptocurinen ja jos k<0 es platicúrtica.

Mikä on roskillinen?

Kostoosi on vaihtelun mitta, jota käytetään jakautumisen morfologian karakterisoimiseksi. Tällä tavoin symmetrisiä jakaumia voidaan verrata samaan keskimääräiseen ja yhtä suureen dispersioon (standardipoikkeama).

Vaihtelevuusmittaukset varmistavat, että keskiarvot ovat luotettavia ja auttavat hallitsemaan jakeluvaihteluita. Analysoidaan esimerkiksi nämä kaksi tilannetta.

3 osaston palkka

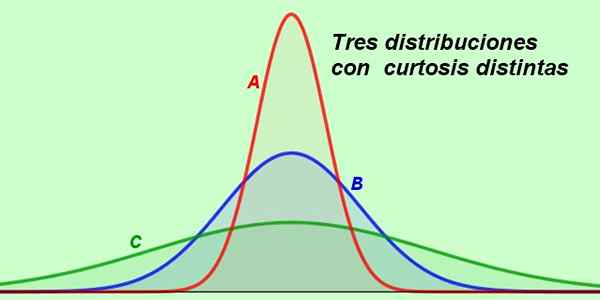
Oletetaan, että seuraava kaavio näyttää jakaumat saman yrityksen 3 osaston palkassa:

Kuva 2. Kolme erilaista jakaumaa kuvaavat käytännön tilanteita. (Valmistaja Fanny Zapata)

Käyrä A on kaikkein hoikka kaikista, ja muodossaan päätellään, että suurin osa kyseisen osaston palkoista on hyvin lähellä keskiarvoa, joten suurin osa työntekijöistä saa samanlaista korvausta.

Voi palvella sinua: kokonaiset numerot

Palkkakäyrä on puolestaan ​​B -osastolla B -osastolla normaalia jakautumista, koska käyrä on mesokuri, jossa oletetaan, että palkat jakautuvat satunnaisesti.

Ja lopuksi meillä on C -käyrä, joka on erittäin litistetty, merkki siitä, että tässä osastolla palkkaalue on paljon laajempi kuin muissa.

Tentin tulokset

Oletetaan nyt, että kuvan 2 kolme käyrää edustavat kokeen tuloksia, joita sovelletaan kolmeen saman aiheen opiskelijaryhmään.

Ryhmä, jonka pätevyyttä edustaa käyrä leptocuriciin, on melko homogeeninen, eniten saatiin keskimäärin tai läheinen luokitus.

On myös mahdollista, että tulos johtui siitä, että tenttikysymyksillä oli enemmän tai vähemmän sama vaikeusaste.

Toisaalta ryhmän C tulokset osoittavat suuremman heterogeenisyyden ryhmässä, joka todennäköisesti sisältää keskimääräisiä opiskelijoita, joitain erinomaisia ​​opiskelijoita ja varmasti toinen vähemmän tarkkaavainen.

Tai se voi tarkoittaa, että testin kysymyksillä oli hyvin erilaisia ​​vaikeuksia.

Käyrä B on mesocurinen, mikä osoittaa, että testitulokset seurasivat normaalia jakaumaa. Tämä on yleensä yleisin tapaus.

Ratkaistu esimerkki Curtosta

Löydä Fisherin osoituskerroin seuraaville arvosanoille, jotka on saatu fysiikkakokeessa opiskelijaryhmälle, asteikolla 1-10:

5, 5, 4, 7, 7,7, 9, 8, 9, 4, 3

Ratkaisu

Seuraavaa lauseketta käytetään ei -ryhmittyneisiin tietoihin, jotka on annettu edellisissä osissa:

Fisher Point -kertoimen kanssa:

Voi palvella sinua: Pythagorean -identiteetit: esittely, esimerkki, harjoitukset

K = g₂ - 3

Tämä arvo sallii tietää jakelutyypin.

G: n laskemiseksi₂ On kätevää tehdä niin järjestettävällä tavalla, askel askeleelta, koska useita aritmeettisia operaatioita on ratkaistava.

Vaihe 1

Ensinnäkin pätevyyden keskiarvo lasketaan. Tietoja on n = 11.

X = (5+5+4+7+7+7+9+8+9+4+3)/11 = 6.182

Vaihe 2

Vakiopoikkeama löytyy, jota varten tätä yhtälöä käytetään:

 Käyttämällä laskinta, jolla on tilastolliset toiminnot, tulos on välitön:

σ = 1.992

Tai voit myös rakentaa taulukon, jota tarvitaan myös seuraavaan vaiheeseen ja johon jokainen tarvittavat yhteenvetojen aikakausi kirjoitetaan, alkaen (x_Yllyttää - X), sitten (x_Yllyttää - X)² Ja sitten (x_Yllyttää - X)⁴ -

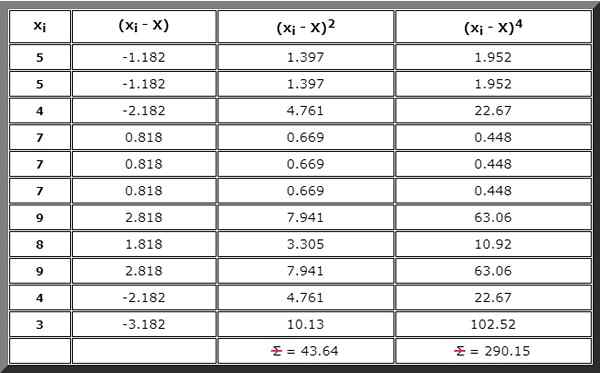
Vaihe 3

Suorita kaavan numeroijalle osoitettu summa G: lle₂. Tätä varten käytetään edellisen taulukon oikean sarakkeen tulosta:

∑ (x_Yllyttää - X)⁴= 290.viisitoista

Siksi:

g₂ = (1/11) x 290.15/1.992⁴ = 1.675

Fisherin opastuskerroin on:

K = g₂ - 3 = 1.675 - 3 = -1.325

Mitkä kiinnostuksen kohteet ovat tuloksen merkki, joka negatiivisena vastaa erilaisten vaikeustasojen tasoa.

Laskentataulukon, kuten Excel, käyttö helpottaa huomattavasti tämäntyyppisten ongelmien ratkaisua ja tarjoaa myös mahdollisuuden kuvaaja jakelu.

Viitteet

1. Levin, r. 1988. Järjestelmänvalvojien tilastot. Toinen. Painos. Prentice Hall.
2. Marco, f. Ryöstö. Toipunut: Econompedia.com.
3. Oliva, J. Epäsymmetria ja rosko. Haettu osoitteesta: StatisticsAucv.Tiedostot.WordPress.com.
4. Spurr, w. 1982. Päätöksen tekeminen hallinnossa. Limusa.
5. Wikipedia. Kurtoosi. Haettu: vuonna.Wikipedia.org.