Todennäköisyys aksioomien tyypit, selitys, esimerkit, harjoitukset

Se aksiomit todennäköisyys Ne ovat matemaattisia ehdotuksia todennäköisyyden teoriasta, jotka eivät ansaitse demonstraatiota. Venäjän matemaatikko Andrei Kolmogorov (1903-1987) perusti aksioomat vuonna 1933 hänen työssään Todennäköisyysteorian perusteet ja loi perustan matemaattiselle tutkimukselle todennäköisyydestä.

Kun suoritat tietyn satunnaisen kokeen ξ, näytetila on se, jolla on yhdessä kokeen mahdollisten tulosten kanssa, joita kutsutaan myös Tapahtumat. Jokainen tapahtuma on merkitty a ja p (a) on todennäköisyys tapahtua. Sitten Kolmogorov totesi, että:

Kuvio 1. Todennäköisyys -aksioomat sallivat laskea pelaamisen todennäköisyyden, kuten ruletti. Lähde: Pixabay.

-Aksiooma 1 (ei negatiivisuutta): Todennäköisyys, että kaikki tapahtumat tapahtuvat, on aina positiivinen tai nolla, P (a) ≥0. Kun tapahtuman todennäköisyys on 0, sitä kutsutaan Mahdoton tapahtuma.

-Axioma 2 (varmuus): edellyttäen, että jokin tapahtuma, joka kuuluu E: lle, sen esiintymisen todennäköisyys on 1, jota voimme ilmaista P (e) = 1. On niin kutsuttu a Turvallinen tapahtuma, Siitä lähtien, kun kokeilun suorittaminen on tulosta kaikesta varmuudesta.

-Axioma 3 (lisäys): Kahden tai useamman yhteensopimattoman tapahtuman tapauksessa kaksi tai kaksi, kutsuttu₁, -Lla₂, -Lla₃..., tapahtuman todennäköisyys₁ Lisää a₂ Lisää a₃ Ja niin edelleen, jokainen tapahtuu todennäköisyyksien summa erikseen.

Tämä ilmaistaan ​​seuraavasti: P (a₁ U a₂ U a₃ U ...) = p (a₁) + P (a₂) + P (a₃) +..

Kuva 2. Venäjän merkittävä matemaatikko Andrei Kolmogorov (1903-1987), joka loi perustan aksiomaattiseen todennäköisyyteen. Lähde: Wikimedia Commons.

[TOC]

Esimerkki

Todennäköisyyden aksioomia käytetään laajasti monissa sovelluksissa. Esimerkiksi:

Kynsi tai tachuela heitetään ilmaan, ja kun lattia putoaa, on mahdollisuus pudota kärjessä (u) tai kärjen ollessa alas (d) (emme harkitse muita mahdollisuuksia). Tämän kokeen näytetila koostuu näistä tapahtumista, sitten e = u, d.

Voi palvella sinua: vallankumous kiinteät aineet: tilavuus, tyypit, ratkaisut harjoituksetKuva 3. Tachuelan käynnistämiskokeessa on kaksi erilaista todennäköisyyttä: putoaa kärjen kanssa tai lattiaan. Lähde: Pixabay.

Soveltamalla aksioomia, joita meillä on:

P (e) = 1 (Axioma 2)

Mutta P (e) = p (u) + p (d) (Axioma 3), koska nämä tapahtumat ovat molemminpuolisesti yhteensopimattomia tai hajoavia. Vika ei pudota kärjen ollessa ylös tai alas samanaikaisesti, se on yksi tai toinen, mutta ei molempia, koska muita mahdollisuuksia harkitaan. Niin:

P (u) + p (d) = 1

P (u) = 1 - p (d)

Jos se todennäköisesti putoaa kärjen ollessa ylös tai alas, P (u) = p (d) = ½ (Axioma 1). Voi kuitenkin olla, että virheen rakentamisen ja suunnittelun vuoksi. Esimerkiksi se voi olla se P (u) = ¾ sillä aikaa P (d) = ¼ (Axioma 1).

Huomaa, että molemmissa tapauksissa todennäköisyyksien summa antaa 1. Aksioomit eivät kuitenkaan tarkoita, kuinka todennäköisyyksiä voidaan jakaa, ainakaan ei täysin. Mutta he vakuuttavat, että ne ovat välillä 0 ja 1, ja se, kuten tässä tapauksessa tapahtuu, kaikkien summa on 1.

Tapoja osoittaa todennäköisyys

Todennäköisyys aksioomit eivät ole menetelmä todennäköisyyden arvon osoittamiseksi. Tätä varten on kolme vaihtoehtoa, jotka ovat yhteensopivia aksioomien kanssa:

Laplace -sääntö

Jokaiselle tapahtumalle annetaan sama todennäköisyys tapahtua, sitten esiintymisen todennäköisyys määritetään seuraavasti:

P (a) = tapahtuman A/ Mahdollisten tapausten määrän tapausten lukumäärä

Esimerkiksi, mikä on todennäköisyys saada ässä ranskalaisten korttien kannesta? Kannella on 52 korttia, 13 jokaisesta sauvasta ja siellä on 4 sauvaa. Jokaisella sauvalla on 1, joten yhteensä on 4 ässää:

P (AS) = 4/52 = 1/13

Laplacen sääntö rajoittuu äärellisiin näytetiloille, joissa jokainen tapahtuma on yhtä todennäköinen.

Voi palvella sinua: Disretillinen matematiikka

Suhteellinen taajuus

Tässä kokeilun on oltava toistettavissa, koska menetelmä perustuu suuren määrän toistojen suorittamiseen.

Tehdään kokeen ξ toistoja, joista havaitsemme, että n on kuinka monta kertaa tietty tapahtuma A, niin todennäköisyys, että tämä tapahtuma tapahtuu, on:

P (a) = lim_{I → ∞} (ei kumpikaan)

Missä N/I on tapahtuman suhteellinen taajuus.

Määritä p (a) tällä tavalla tyydyttää Kolmogorovin aksioomit, mutta sillä on haittaa, että monet testit on suoritettava siten, että todennäköisyys on tarkoituksenmukaista.

Subjektiivinen menetelmä

Henkilö tai ihmisryhmä voi suostua antamaan todennäköisyyden tapahtumaan omien tuomioidensa kautta. Tällä menetelmällä on haitta, että eri ihmiset voivat antaa erilaiset todennäköisyydet samaan tapahtumaan.

Liikuntaa

Kokeessa samanaikaisesti kolmen rehellisen valuutan käynnistäminen, kuvattujen tapahtumien mahdollisuuden hankkiminen:

a) 2 kasvot ja risti.

b) 1 kasvot ja kaksi ristiä

c) 3 ristiä.

d) Ainakin yksi kasvot.

Liittää jhk

Kasvot on merkitty C: llä ja ristillä x: n kanssa. Mutta on olemassa useita tapoja saada kaksi kasvoja ja risti. Esimerkiksi kaksi ensimmäistä kolikkoa voivat pudota kasvojen kanssa ja kolmas Cruzin kanssa. Tai ensimmäinen voi pudota kasvot, toinen risti ja kolmas kasvot. Ja lopuksi ensimmäinen voi olla risti ja jäljellä olevat kasvot.

Kysymyksiin vastaamiseksi on tarpeen tietää kaikki mahdollisuudet, jotka on kuvattu työkalussa nimeltään puukaavio jompikumpi Todennäköisyyspuu-

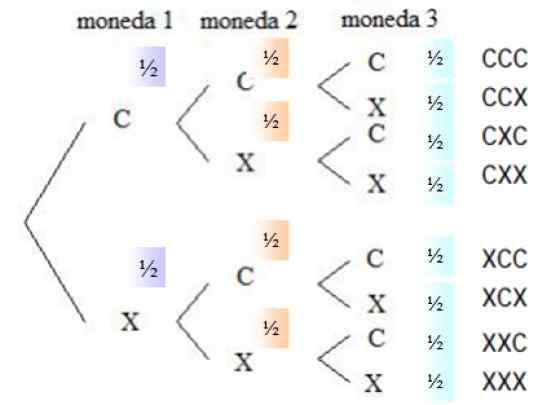Kuva 4. Puukaavio kolmen rehellisen kolikon samanaikaisesta käynnistämisestä. Lähde: f. Zapata.

Todennäköisyys, että missä tahansa valuutassa on kallis, on ½, sama tapahtuu risteille, koska valuutta on rehellinen. Oikeassa sarakkeessa kaikki käynnistämismahdollisuudet on lueteltu, ts.

Voi palvella sinua: Tilastolliset muuttujat

Pyydettyyn tapahtumaan reagoivat yhdistelmät valitaan näytetilasta, koska kasvot näyttävät. Suotuisia tapahtumia on kolme: CCX, CXC ja XCC. Kunkin tapahtuman todennäköisyys on:

P (ccx) = ½. ½ . ½ = 1/8

Sama tapahtuu CXC- ja XCC -tapahtumille, jokaisella on 1/8 todennäköisyys tapahtua. Siksi 2 pinnan saamisen todennäköisyys on kaikkien suotuisten tapahtumien todennäköisyyksien summa:

P (2 kasvot) = 1/8 + 1/8 + 1/8 = 3/8 = 0.375

Ratkaisu b

Löydä todennäköisyys, että kaksi ristiä on tarkalleen, on analoginen ongelma edelliselle, näytetilasta on myös kolme suotuisaa tapahtumaa: CXX, XCX ja XXC. Siksi:

P (2 ristiä) = 3/8 = 0.375

Liuos C

Intuitiivisesti tietävät, että 3 ristien (tai 3 pinnan) saamisen todennäköisyys on alhaisempi. Tässä tapauksessa etsitty tapahtuma on XXX, oikean sarakkeen lopussa, jonka todennäköisyys on:

P (xxx) = ½. ½. ½ = 1/8 = 0.125.

Liuos D

Sitä pyydetään hankkimaan vähintään yksi kasvot, tämä tarkoittaa, että 3 kasvot, 2 kasvot tai 1 kasvot voivat lähteä. Ainoa tämän kanssa ristiriitainen tapahtuma on yksi, jossa 3 ristiä tulee esiin, jonka todennäköisyys on 0.125. Siksi etsitty todennäköisyys on:

P (vähintään yksi kasvo) = 1 - 0.125 = 0.875.

Viitteet

1. Canavos, G. 1988. Todennäköisyys ja tilastot: Sovellukset ja menetelmät. McGraw Hill.
2. DeVore, J. 2012. Tekniikan ja tieteen todennäköisyys ja tilastot. Kahdeksas. Painos. Kyynärmä.
3. Lipschutz, S. 1991. Schaum -sarja: todennäköisyys. McGraw Hill.
4. Obregón, minä. 1989.Todennäköisyyden teoria. Toimituslimusa.
5. Walpole, r. 2007. Tekniikan ja tieteen todennäköisyys ja tilastot. Pearson.