Säännölliset, epäsäännölliset dekagonit, ominaisuudet, esimerkit

Hän dekangoni Se on litteä kuva, jossa on monikulmiokuorinen 10 sivua ja 10 kärkiä tai kärkeä. Decagens voi olla säännöllisiä tai epäsäännöllisiä, ensimmäisessä tapauksessa kaikilla puolilla ja sisäkulmissa on sama mitta, kun taas toisessa sivut ja/tai kulmat eroavat toisistaan.

Kuvio 1 esittää esimerkkejä kunkin tyypin dekagoneista ja kuten näemme, tavallinen dekagoni on erittäin symmetrinen.

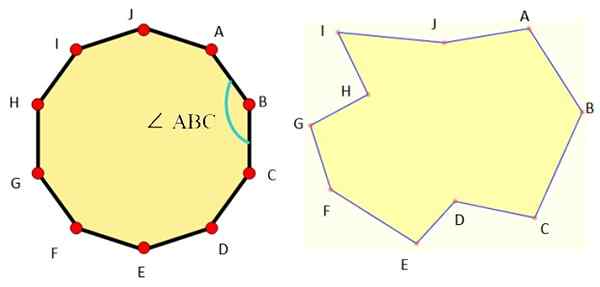Kuvio 1. Vasemmalle tavallinen dekagoni ja oikealla epäsäännöllinen dekagoni. Lähde: Wikimedia Commons/F. Zapata/MathPenref.

Kaikkien dekagonien peruselementit ovat:

-Sivut, linjasegmentit, jotka liittyivät dekagoniin.

-Kärjet tai pisteet kunkin peräkkäisen puolen välillä.

-Viereisten sivujen väliset sisäiset ja ulkoiset kulmat.

-Diagonaalit, segmentit, jotka yhdistävät kaksi ei -säilytystilaa.

Kärkipisteitä kutsutaan isoilla kirjaimilla, kuten kuvassa 1 esitetään, joissa käytettiin aakkosten ensimmäisiä kirjaimia, mutta mitä tahansa kirjainta voidaan käyttää.

Sivut symboloidaan kahdella kärkipisteellä. Samalla tavalla se tehdään diagonaalien kanssa, joten meillä on diagonaali AF, joka liittyy pisteisiin A ja F.

Kulmissa käytämme tätä symbolia: ∠, samanlainen kuin kalteva L. Esimerkiksi kulma ∠ ABC on sellainen, jonka kärki on B ja joiden sivut ovat AB- ja BC -segmentit.

[TOC]

Säännöllinen dekagoni

Tavallisessa dekagonissa kaikilla puolilla on sama mitta, samoin kuin sisäkulmat. Siksi sen sanotaan olevan tasasivuinen (yhtä suuret puolet) ja tasa -arvoinen (Yhtä suuret kulmat). Se on erittäin symmetrinen hahmo

Säännöllisen dekagonin sisäkulmat

Käytetään seuraavaa kaavaa, jotta voidaan löytää tavallisen monikulmion, mukaan lukien tavallinen dekagoni, mittaa: tavallinen dekagoni:

Missä:

-I on kulman mitta asteina.

-n on monikulmion sivujen lukumäärä. Decagonin tapauksessa n = 10.

Voi palvella sinua: Heptagon

Korvaamalla n = 10 edellisestä kaavasta saamme seuraavan:

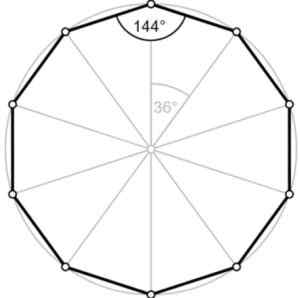
Nyt sanotaan, että monikulmio on kupera Jos sen kulmamittaukset ovat alle 180º, muuten monikulmio on kovera. Kuten minkä tahansa säännöllisen dekagonin sisäkulma on 144º ja on alle 180º, niin se on kupera monikulmio.

Sisäkulmien summa

Minkä tahansa monikulmion sisäkulmien mittausten summa on asteina:

S = (n-2) x 180º; n on aina suurempi kuin 2

Tässä kaavassa meidän on:

-S on sisäisten kulmien mittausten summa.

-n on sivujen lukumäärä. Dekagonille n = 10

Kaavan soveltaminen n = 10 tulokseen:

S = (10 - 2) x 180º = 1440º

Ulkokulmat 

Yhden sivun ja viereisen puolen pidennyksen väliin muodostuu ulkokulma: Katsotaanpa:

Kuva 2.- Säännöllisen dekaanin ulkoinen kulma on 36º. Suihkulähde. Wikimedia commons/f. Zapata.

Kulma ∠ ABC plus ulkoinen kulma lisää 180º, ts. Ne ovat Lisä-. Siksi ulkoinen kulma on yhtä suuri kuin 180º-144º = 36º, kuten kuvassa näemme.

Diagonaalien lukumäärä

Kuten aiemmin todettiin, diagonaalit ovat segmenttejä, jotka yhdistävät ei -säilytyskipuja. Kuinka monta diagonaalia voimme jäljittää dekagonissa? Kun kärkipisteiden lukumäärä on pieni, ne voidaan helposti laskea, mutta kun määrä kasvaa, voit menettää tilin.

Onneksi on kaava, jolla tiedetään monikulmion diagonaalien lukumäärä n sivut:

Decagonille korvaamme n = 10 ja saamme:

D = 10 x (10 - 3) /2 = 35

Tavallisessa dekagonissa kaikki diagonaalit leikataan yhdessä pisteessä, mikä on kuvan keskipiste:

Kuva 3. Tavallisen dekaanin kulmat ja diagonaalit. Lähde: Wikimedia Commons.

Keskusta

Monikulmion keskipiste määritellään minkä tahansa kärjen tasa -arvoiseksi pisteeksi. Edellisessä kuvassa keskus osuu kaikkien diagonaalien leikkauspisteen kanssa.

Kehä

Jos tavallisella dekagonilla on puoli A, sen kehä P on kaikkien osapuolten summa:

Voi palvella sinua: 90 jakajaa: Mitkä ovat ja selitys

P = 10.-lla

Alue

Tietäen pituuden -lla Sivulla säännöllinen dekagonialue lasketaan:

Arvioitu kaava alueelle on:

Ja kolmas vaihtoehto löytää alueen apoteemin l pituuden kautta_-Lla. Tämä on segmentti, joka liittyy keskipisteeseen toisella puolella monikulmion keskustan kanssa.

Tässä tapauksessa alue voidaan laskea kaavalla:

Epäsäännöllinen dekagoni

Epäsäännöllinen dekagoni ei ole tasapainon tai etäisyys, ja yleensä siitä puuttuu tavanomaisen hahmon symmetria, vaikka joillakin dekoneilla voi olla symmetria -akselia.

Ne voivat myös olla kupera tai kovera, jos sisäkulmat ovat suurempia kuin 180º.

Kuvion 1 epäsäännöllinen dekagoni on kovera, koska jotkut sen sisäkulmista ovat suurempia kuin 180º. On selvää, että on olemassa monia kulmien ja sivujen yhdistelmiä, jotka aiheuttavat epäsäännöllisen dekagonin.

Joka tapauksessa on toteutettu, että:

-Myös epäsäännöllisen dekagonin sisäkulmat lisäävät 1440º.

-Siinä on myös 35 diagonaalia.

Gauss -determinantit

Yleensä ei ole ainutlaatuista kaavaa löytää epäsäännöllisen monikulmion alue, koska sivut ja kulmat ovat erilaisia. Löydät kuitenkin kärkipisteiden koordinaattien tuntemuksen ja laskemisen Gauss -determinantit-

-Soitetaan (x_n , ja_n ) Paritsien koordinaateille n vaihtelee välillä 1-10.

-Voit aloittaa mistä tahansa kärkipisteestä, mihin koordinaatit määritetään (x x₁, ja₁ -A. Nyt sinun on korvattava kunkin koordinaatin arvot tässä kaavassa:

Missä determinantit ovat juuri sulujen välisiä operaatioita.

-On tärkeää huomata, että viimeinen determinantti sisältää ensimmäisen kärjen yhdessä viimeisen kanssa. Decagonille se olisi näin:

(x₁₀ja₁ - x₁ja₁₀-A

Voi palvella sinua: LaGrange -interpolointi

Tärkeä: Pylväät ovat absoluuttisen arvon ja tarkoittavat, että lopputulos on aina positiivinen merkki.

Menettely voi olla työläs, kun kuvassa on monia kärkipisteitä, dekagonin tapauksessa on 10 operaatiota, joten on suositeltavaa tehdä taulukko tai luettelo.

Liikuntaa

Laske kuvassa esitetty epäsäännöllinen dekagonialue. Perictices -koordinaatit ovat A, B, C ... J, joiden arvot on esitetty vasemmalla.

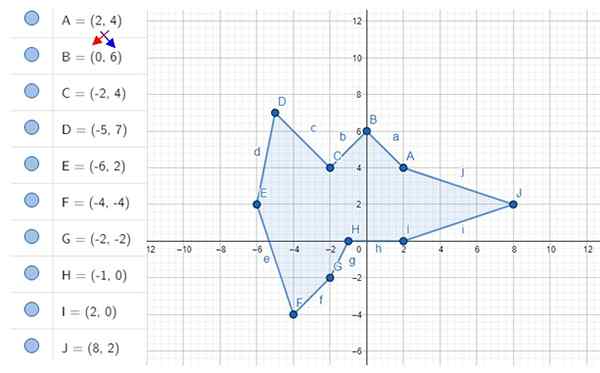Kuva 4. Epäsäännöllinen dekagoni ja sen kärjet. Lähde: f. Zapata geogebralla.

Ratkaisu

-Teemme jokaisen 10 toiminnan:

• 2 × 6 - 4 × 0 = 12 - 0 = 12
• 0 × 4 - 6 × (-2) = 0 + 12 = 12
• (-2) × 7-4 × (-5) = -14 + 20 = 6
• (-5) × 2 -7 × (-6) = -10 + 42 = 32
• (-6) × (-4) -2 × (-4) = 24 + 8 = 32
• (-4) × (-2)-(-4) × (-2) = 8-8 = 0
• (-2) × 0-(-2) × (-1) = 0 -2
• (-1) × 0 - 0 × (2) = 0 - 0 = 0
• 2 × 2 - 0 × 8 = 4 - 0 = 4
• 8 × 4 -2 × 2 = 32 - 4 = 28

-Lisäämme tulokset:

12 + 12 + 6 + 32 + 32 + 0 + (-2) + 0 + 4 + 28 = 124

Positiivinen tulos saadaan jopa ilman absoluuttisen arvon palkkeja, mutta jos se on negatiivinen, sama muutetaan.

-Aikaisempi tulos on jaettu 2: lla ja se on monikulmion alue:

A = 124/2 = 62

Decangon -ominaisuudet

Alla on yhteenveto dekagonin yleisistä ominaisuuksista, joko säännöllinen tai epäsäännöllinen:

-On 10 sivua ja 10 kärkeä.

-Sisäkulmien summa on 1440º.

-Diagonaaleja on 35.

-Kehä on kaikkien osapuolten summa.

-Voit luoda kolmioita monikulmion piirustussegmenttien sisällä kärkipisteestä kaikille muille. Decagonissa on mahdollista piirtää 8 kolmiota tällä tavalla, kuten alla on esitetty:

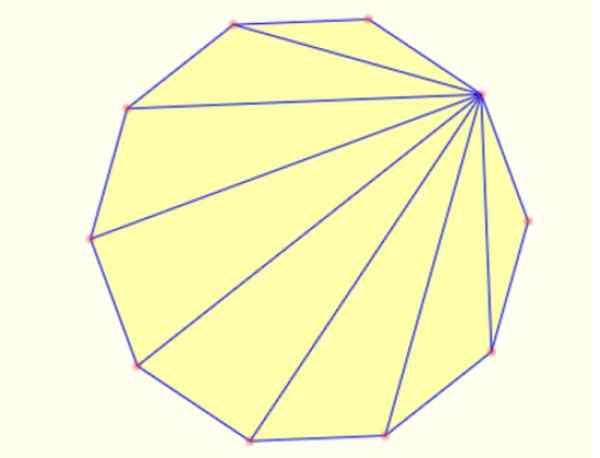Kuva 5. Sisäiset kolmiot tavallisessa dekagonissa. Lähde: MathPenref.

Viitteet

1. Alexander, D. 2013. Geometria. Viides. Painos. Cengage -oppiminen.
2. Dekangoni.com. Dekangoni. Toipunut: Decagon.com
3. Matematiikan avoin viite. Dekangoni. Toipunut: MathPenref.com.
4. Sangaku -matematiikka. Monikulmion ja sen luokituksen elementit. Toipunut: Sangakoo.com.
5. Wikipedia. Dekangoni. Palautettu: on.Wikipedia.com.