Suhteellisen tiheyden laskenta, esimerkit, harjoitukset

Se Suhteellinen tiheys Se on yhden aineen tiheyden ja toisen viitteen tiheyden ja toisen vertailun suhde 4 ° C: ssa (39.2 ºF) nesteille ja kiinteille aineille, kun taas kaasujen kuivaa ilmaa käytetään.

Joissakin teksteissä sitä kutsutaan myös Tietty painovoima (kirjaimellinen käännös Tietty painovoima englanniksi), mutta se on sama käsite. Molempien tiheyksien on oltava samassa yksikköjärjestelmässä ja ne on mitattu samoissa paine- ja lämpötila -olosuhteissa.

Kelluvien esineiden suhteellinen tiheys on vähemmän kuin veden tiheä. Lähde: Pixabay.

Suhteellinen tiheys lasketaan matemaattisesti seuraavasti:

Suhteellinen tiheys = veden veden tiheys/

Vaikka minkä tahansa aineen tiheys riippuu paine- ja lämpötilaolosuhteista, joissa sitä mitataan, etenkin kun kyse on kaasuista, suhteellinen tiheys on erittäin hyödyllinen käsite erilaisten materiaalien karakterisoimiseksi nopeasti.

Seuraavaksi tätä arvostetaan, koska vesitiheys on noin 1 grammaa kuutiometriä kohti: 1 g /cm3 tai 1000 kg /m³, Ilmakehän paineella ja hyvällä lämpötila -alueella (0 - 15 ° C).

Antamalla aineen suhteellisen tiheyden, on heti tiedossa, kuinka kevyt tai raskas veden suhteen, yleinen aine.

Lisäksi suhteellinen tiheys on helppo muistaa, koska se mitataan pienellä ja helppo käsitellä numeroita, kuten seuraavassa osassa nähdään, joissa on mainittu suhteellisten tiheyksien arvot joillekin tunnetuille aineille.

[TOC]

Esimerkit

Veden suhteellinen tiheys on selvästi 1, koska kuten alussa todettiin, se on nesteiden ja kiinteiden aineiden referenssikuvio. Nesteillä, kuten kahvilla, maito- tai virvoitusjuomilla, on suhteellisen tiheys hyvin lähellä vettä.

Öljyjen suhteen kaikkiin sovellettavan suhteellisen tiheyden ainutlaatuista arvoa, koska se riippuu sen alkuperästä, koostumuksesta ja käsittelystä. Useimmat suhteellisimmat öljytiheydet ovat 0.7 ja 0.95.

Voi palvella sinua: Watt Law: Mikä on, esimerkkejä, sovelluksia

Kaasut ovat paljon kevyempiä, joten monissa sovelluksissa viite on ilman tiheys, joten suhteellinen tiheys osoittaa, kuinka kevyt tai raskas kaasu ilmassa suhteessa. Verrattuna ilman suhteellinen tiheys on 0.0013.

Tarkastellaan joitain suhteellisia tiheysarvoja tunnetuille aineille ja materiaaleille.

Joidenkin tunnettujen aineiden suhteellinen tiheys

- Ihmiskeho: 1.07.

- Elohopea: 13.6.

- Glyseriini: 1.26.

- Bensiini: 0.68.

- Merivesi: 1.025.

- Teräs: 7.8.

- Puu: 0.5.

- Jää: 0.92.

Suhteellisen tiheyden arvo ilmoittaa välittömästi, kelluuko aine tai materiaali vedessä vai päinvastoin.

Tämän vuoksi öljykerros on veden päällä, koska melkein kaikkien öljyjen suhteellinen tiheys on vähemmän kuin tämän nesteen tiheä. Puinen kuutio vedessä voi olla siitä ulos, samalla tavalla kuin jää.

Ero absoluuttisen tiheyden kanssa

Absoluuttinen tiheys on osamäärä aineen massan ja sen käyttämänsä määrän välillä. Koska tilavuus puolestaan ​​riippuu lämpötilasta (kun suurin osa aineista on laajennettu) ja paineesta, tiheys puolestaan ​​riippuu näistä kahdesta suuruudesta. Matemaattisesti sinulla on:

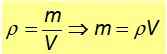
Missä ρ on tiheys, jonka yksiköt kansainvälisessä järjestelmässä ovat kg/m³, m on taikina ja V Se on tilavuus.

Taulukoissa näkyvien absoluuttisen tiheyden arvot määritetään yleensä ilmakehän paineessa ja tietyillä lämpötila -alueilla johtuen suhteesta lämpötilaan ja paineen määrään.

Voi palvella sinua: fyysinen optiikka: historia, usein termit, lait, sovellukset

Siten kaasujen normaaleissa olosuhteissa: 1 paineen ilmapiiri ja 0º C lämpötila, ilman tiheys määritetään 1.293 kg/m³.

Vaikka sen arvo kokee nämä variaatiot, se on erittäin sopiva määrä aineiden käyttäytymisen määrittämiseksi, etenkin jatkuvina keinoin.

Ero suhteellisen tiheyden kanssa on, että absoluuttisella on mitat, jolloin sen arvot riippuvat valittujen yksiköiden järjestelmästä. Tällä tavoin vesitiheys lämpötilan 4. C: n kohdalla on:

ρ_vettä = 1 g /cm³ = 1000 kg/m³ = 1.94 etana/jalka³

Ratkaisut

-Harjoitus 1

Löydä tilavuus, jota miehittää 16 grammaa öljyä, jonka suhteellinen tiheys on 0.8.

Ratkaisu

Ensin löydämme absoluuttisen tiheyden ρ_öljy öljyä. Merkitsee miten s_g Sen suhteellinen tiheys on:

ρ_öljy = 0.8 x vesitiheys

Vesitiheyden kannalta edellisessä osassa annettua arvoa käytetään. Kun suhteellinen tiheys tiedetään, absoluuttinen palautetaan välittömästi kertomalla tämä arvo vesitiheydellä. Niin:

Materiaalitiheys = suhteellinen tiheys x Vesitiheys (normaaleissa olosuhteissa).

Siksi tämän esimerkin öljylle:

ρ_öljy = 0.8 x 1 g/cm³= 0.8 g/cm³

Koska tiheys on massa m ja osa V, tämä pysyy seuraavasti:

V = m/ρ = 16 g / 0.8 g/cm³= 20 cm³

-Harjoitus 2

Kallion erityinen painovoima on 2.32 ja tilavuus 1.42 x 10 ^-4 m³. Löydä kallion paino kansainvälisen järjestelmän yksiköistä ja teknisestä järjestelmästä.

Ratkaisu

Vesitiheysarvoa käytetään 1000 kg/m³-

Se voi palvella sinua: Maan käännösliike

ρ_rock = 2.32 x 1000 kg/m³= 2.32 x 10³ Kg/m³

Massa m kalliosta on kilogrammissa:

M = r -_rock . V = 2.32 x 10³ Kg/m³. 1.42 x 10 ^-4 m³ = 0.33 kg.

Paino teknisen järjestelmän yksiköissä on 0.33 kiloa voimaa. Jos kansainvälisessä järjestelmässä on suositeltavaa, yksikkö on Newton, jolle massa kerrotaan G: n arvolla, painovoiman kiihtyvyys.

P = m. G = 0.33 kg. 9.8 m/s² = 3.23 n.

-Harjoitus 3

Piknometri on säiliö, jonka kanssa aineen suhteellinen tiheys tietyssä lämpötilassa voidaan määrittää.

Pyknometri. Lähde: Wikipedia.org.

Laboratoriossa tuntemattoman nesteen tiheyden määrittämiseksi noudatettiin tätä menettelyä:

- Tyhjä piknometri punnittiin ja lukeminen oli 26.038 g

- Sitten piknometri vedellä 20º C (vesitiheys 0.99823 g/cc) ja punnittu, saadaan arvo 35.966 g.

- Lopuksi pikknometri, joka oli täynnä tuntemattomia nesteitä, punnittiin ja saatu lukeminen oli 37.791 g.

Lauseke pyydetään määrittämään nesteen tiheyden laskemiseksi ja soveltamaan sitä saatuihin tietoihin.

Ratkaisu

Sekä veden että nesteen massa määritetään vähentämällä piknometrin lukeminen, joka on täynnä tyhjän piknometriä:

massa _H2O = 35.966 g - 26.038 g = 9.928 g; massa _sujuva  = 37.791 g - 26.038 g = 11.753 g

Lopuksi se korvataan johdetussa lausekkeessa:

ρ_sujuva = (11.753 g / 9.928 g) . 0 -.99823 g/cc = 1.182 g/cm3.

Viitteet

1. Brittiläinen tietosanakirja. Tietty painovoima. Toipunut: Britannica.com.
2. Giancoli, D.  2006. Fysiikka: sovellusten periaatteet. 6^th… Ed Prentice Hall.
3. Mott, r.  2006. Fluidimekaniikka. Neljäs. Painos. Pearson -koulutus. 12-21.
4. Valera Negrete, J. 2005. Yleiset fysiikan muistiinpanot. Yksinäinen. 44-45.
5. Valkoinen, f. 2004. Fluidimekaniikka. 5. painos. MC Graw Hill. 17-18.