Antoine -kaavojen, yhtälöiden, esimerkkien vakiot

Se Antoine -vakiot On olemassa kolme parametria, jotka esiintyvät empiirisessä suhteessa kyllästymishöyrynpaineen ja puhtaan aineiden lämpötilan välillä. Ne riippuvat jokaisesta aineesta ja niiden oletetaan olevan vakio tietyllä lämpötilan alueella.

Tältä alueelta Antoine -vakiot muuttavat arvonsa. Vakiot liittyvät ranskalaisen insinöörin Louis Charles Antoine (1825-1897) vuonna 1888 luoman yhtälön kautta vuonna 1888, jonka on luonut vuonna 1888.

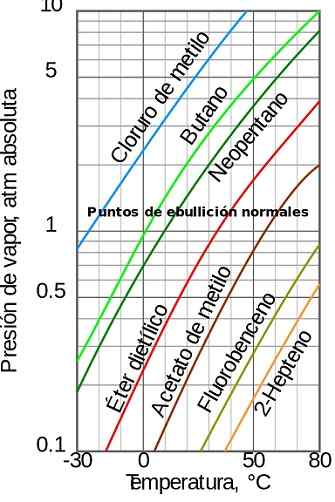
Kuvio 1. Höyrynpaine lämpötilasta riippuen. Lähde: Wikimedia Commons

[TOC]

Kaavat ja yhtälöt

Tavallisin tapa ilmaista Antoine -toiminto on:

 

Tässä kaavassa P se edustaa elohopean millimetreissä (MMHG) ilmaistusta kyllästyshöyrynpainetta, t on lämpötila, joka on riippumaton muuttuja ja ilmaistaan ​​℃: ssä. 

A, B ja C ovat Antoine -kaavan vakiot tai parametrit.

Tämän kaavan merkitys, joka on empiirinen huolimatta, antaa yksinkertaisen analyyttisen ekspression, jota voidaan helposti käyttää termodynaamisissa laskelmissa.

Antoinen kaava ei ole ainutlaatuinen, on olemassa tarkempia lausekkeita, jotka ovat tämän kaavan pidennyksiä, mutta haittalla on kuusi tai enemmän parametria ja niiden matemaattinen ilmaisu on monimutkaisempi, mikä tekee niistä erittäin käytännöitä käytettäväksi termodynaamisissa laskelmissa.

Kyllästyshöyry

Kun Antoinen kaava mittaa kylläisyyden höyrynpainetta, on välttämätöntä selittää, mistä se koostuu.

Lasi -ampullissa tai muussa astiassa neste asetetaan. Kaikki ilma on uutettu. Sarja sijoitetaan lämpöhauteeseen, kunnes tasapaino on saavutettu.

Alussa kaikki on nestettä, mutta koska tyhjiö on, nopeimmat molekyylit alkavat luopua nesteen kaasun muodostavan nesteen muodostavan nesteen muodostavan nesteen.

Voi palvella sinua: Yhtenäinen suorakulmainen liike: Ominaisuudet, kaavat, harjoitukset

Edellinen prosessi on haihtuminen Ja kun höyryn paine kasvaa. 

Jotkut höyrymolekyyleistä menettävät energian ja palaavat aineen nestemäiseen vaiheeseen, tämä on prosessi tiivistyminen.

Sitten kaksi prosessia, haihtuminen ja tiivistyminen tapahtuvat samanaikaisesti. Kun sama määrä siihen sisällytettäviä nestemolekyylejä tulee esiin, a dynaaminen tasapaino Ja tällä hetkellä tapahtuu maksimaalinen höyrypaine, joka tunnetaan kyllästyspaineeksi.

Juuri tämä höyryn kylläisyyspaine ennustaa jokaiselle aineelle antoine -kaavan ja jokaiselle lämpötilalle.

Joissakin kiinteissä aineissa on samanlainen ilmiö, kun se kulkee kiinteästä faasista soodaan suoraan käymättä nestefaasin läpi, näissä tapauksissa kyllästymishöyrypaine voidaan myös mitata.

Teoreettisen mallin luominen ei ole helppoa varhaisista periaatteista alkaen, koska molekyylin kineettisen energian muutokset ovat mukana, mikä voi olla translaatio-, kierto- ja värähtelytyyppiä, sisäisen molekyylisidoksen energian kanssa. Tästä syystä käytetään käytännössä empiirisiä kaavoja.

Kuinka Antoine -vakio?

Antoinen vakioiden saamiseksi ei ole teoreettista menetelmää, koska se on empiirinen suhde.

Ne saadaan kunkin aineen kokeellisista tiedoista ja kolmen parametrin A, B ja C säätämisestä siten, että ne minimoivat ennusteen neliömäisen eron (neliömäisten minimien menetelmä) kokeellisen datan kanssa.

Loppukäyttäjälle, jotka ovat yleensä kemiallisia insinöörejä.

Voi palvella sinua: Resistanssilämpömittari: Ominaisuudet, toiminta, käyttö

Saatavana on myös verkkopalveluita, jotka antavat vakioiden A, B ja C arvot, kuten DDBST GmbH onlines -palvelut.

Saman aineen kohdalla voi olla useampi kuin yksi pätevyyslämpötila. Sitten työalueesta riippuen valitaan yksi tai toinen vakioryhmä.

Vaikeudet voivat ilmetä, jos lämpötilatyöalue on vakioiden kahden pätevyysalueen välillä, koska kaavan paineen ennusteet eivät ole samaan aikaan rajavyöhykkeellä.

Esimerkit

Esimerkki 1

Etsi vesihöyrynpaine 25 ℃.

Ratkaisu 

Kuulimme taulukoita Antoinen vakioiden määrittämiseksi.

Vesialueita on kaksi: 

Välillä 1 - 100 ℃ ja välillä 99 - 374 ℃.

Koska olemme kiinnostuneita 25 ℃, otamme ensimmäisen alueen, jolla Antoinen vakioiden arvo on:

A = 8,07131

B = 1730,63

C = 233 426

P = 10^(8 07131 - 1730,63/(25 + 233 426)))

Eksponentin laskenta

Lasketaan ensin eksponentti: 1 374499

P = 10^1 374499 = 23 686 mmHg = 0,031166 ATM

Tulosanalyysi

Tulokset tulkitaan seuraavasti:

Oletetaan.

Veden säiliö asetetaan lämpöhauteeseen lämpötilassa 25 ℃, kunnes lämpötasapaino saavuttaa.

Hermeettisen astian vesi haihtuu osittain, kunnes kyllästymishöyryn paine on saavutettu, mikä ei ole muuta kuin paine, jossa veden nestemäisen vaiheen ja höyryfaasin välinen dynaaminen tasapaino muodostuu. 

Voi palvella sinua: Dirac Jordan Atomic -malli: Ominaisuudet ja postulaatit

Tämä paine tässä tapauksessa osoittautui 0,031166 atm 25 ℃.

Esimerkki 2

Etsi vesihöyrynpaine 100 ℃.

Ratkaisu 

Kuulimme taulukoita Antoinen vakioiden määrittämiseksi. Vesialueita on kaksi: 

Välillä 1 - 100 ℃ ja välillä 99 - 374 ℃.

Tässä tapauksessa kiinnostava lämpötila on kahdella alueella.

Käytämme ensimmäistä aluetta [1 ℃, 100 ℃]

A = 8,07131

B = 1730,63

C = 233 426

P = 10^(8 07131 - 1730,63/(100 + 233 426)))

Eksponentin laskenta

Lasketaan ensin eksponentti: 2.8808

P = 10^1 374499 = 760,09 mmHg = 1 0001 atm

Seuraavaksi käytämme toista aluetta [99 ℃, 374 ℃]

Tässä tapauksessa vakiot ovat

A = 8 14019

B = 1810.94

C = 244.485

P = 10^(8.14019 - 1810.94/(100 + 244.485))

Lasketaan ensin eksponentti: 2.88324

P = 10^2.88324 = 764.2602 mmHg = 1 0056 atm

Kahden tuloksen välillä on prosentuaalinen ero 0,55%.

Viitteet

1. Raoultin ja Daltonin lakien ja Antoine -yhtälön soveltaminen. Haettu: oma ja muinainen.WordPress.com
2.  Antoine -kaavan online -laskin. Toipunut: ddbonline.DDBST./antoineekalcion/antoinecalculaticgi.exe
3. Gecousb. Termodynamiikka ja höyrytaulukot / vakio Antoinista. Toipunut: gecousb.com.mennä
4. Aineen lämpöominaisuudet. Palautettu: verkkopalvelin.DMT.Kisko.On
5. Yaws ja Yang. Antoine -vakiotaulut yli 700 orgaaniselle yhdisteelle. Palautettu: Käyttäjä.Eng.Umd.Edu
6. Wikipedia. Antoine -yhtälö. Toipunut Wikipediasta.com
7. Wikipedia. Clausius-Clapeyron-yhtälö. Toipunut Wikipediasta.com
8. Wisniak J. Dalton Lelu Antoine -höyrypaineyhtälön historiallinen kehitys. Palautettu: linkki.Jousto.com