Peräkkäiset johdannaiset

Mitkä ovat peräkkäiset johdannaiset?

Se peräkkäiset johdannaiset Ne ovat peräisin toiminnasta toisen johdannaisen jälkeen. Prosessi peräkkäisten johdannaisten laskemiseen on seuraava: On funktio F, jonka voimme johtaa ja saada johdetun funktion f '. Tähän f -johdannaiseen voimme saada sen uudelleen, hankkimalla (f ')'.

Tätä uutta toimintoa kutsutaan toiseksi johdannaiseksi; Kaikki toisesta lasketut johdannaiset ovat peräkkäisiä; Näillä, joita kutsutaan myös korkeamman asteen, on suuria sovelluksia, kuten tiedon antaminen funktion kuvaajan iskusta, toisen johdannaisen testin suhteellisille päille ja äärettömän sarjan määrittäminen.

Määritelmä

Leibniz -merkinnän avulla meillä on, että "y" -funktion johdannainen suhteessa "x" on dy/dx. Ilmaista "Y" toiseen johdannaiseen Leibnizin merkintää käyttämällä seuraavasti:

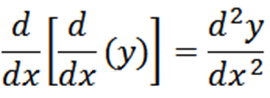
Yleensä voimme ilmaista peräkkäisiä johdannaisia ​​seuraavasti Leibnizin merkinnällä, jossa n edustaa johdannaisen järjestystä.

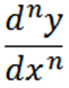
Muut käytetyt merkinnät ovat seuraavat:

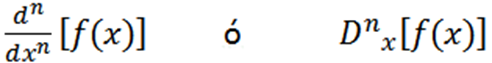
Joitakin esimerkkejä, joissa näemme eri merkinnät:

Esimerkki 1

Hanki kaikki F -funktion johdannaiset määritelty:

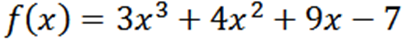
Tavallisten lähetystekniikoiden avulla meillä on, että F on:

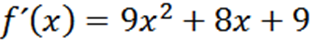
Prosessin toistaminen voimme saada toisen johdannaisen, kolmannen johdannaisen ja niin edelleen.

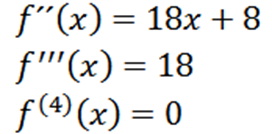
Huomaa, että neljäs johdannainen on nolla ja nollajohdannainen on nolla, joten meidän on:

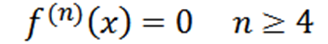
Esimerkki 2

Laske seuraavasta toiminnasta johdettu neljäs:

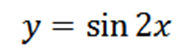
Seurauksena on, että annettu toiminto meillä on:

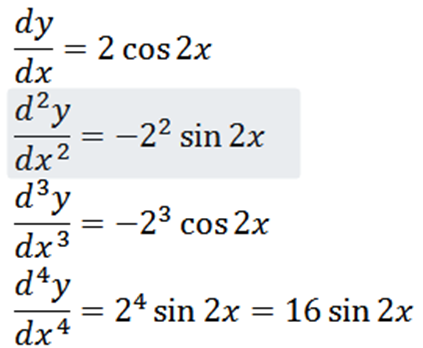
Nopeus ja kiihtyvyys

Yksi johdannaisen löytämiseen johtaneista motivaatioista oli välittömän nopeuden määritelmän etsiminen. Muodollinen määritelmä on seuraava:

Voi palvella sinua: Primo -numerot: Ominaisuudet, esimerkit, harjoitukset

Olkoon y = f (t) funktio, jonka kuvaaja kuvaa hiukkasen etenemissuuntaista t, Sitten hänen nopeutensa välittömässä T: ssä annetaan:

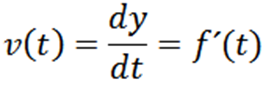
Kun hiukkasen nopeus on saatu, voimme laskea välittömän kiihtyvyyden, joka on määritelty seuraavasti:

Hiukkasen välitön kiihtyvyys, jonka etenemissuunta on annettu y = f (t), on:

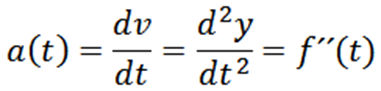
Esimerkki 1

Hiukkas liikkuu viivalla sijaintifunktion mukaan:

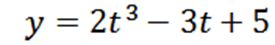
Missä "y" mitataan metreinä ja "T" sekunneissa.

• Millä hetkellä nopeutesi on 0?
• Millä hetkellä sen kiihtyvyys on 0?

Laittamalla Y -sijaintitoiminto meillä on, että sen nopeus ja kiihtyvyys annetaan vastaavasti:

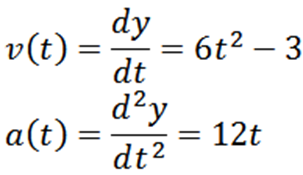
Ensimmäiseen kysymykseen vastaamiseksi riittää määrittämään, milloin V -funktio V on nolla; Tämä on:

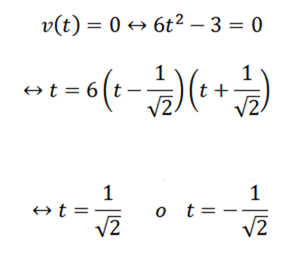
Jatkamme seuraavaa kysymystä analogisesti:

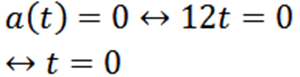
Esimerkki 2

Hiukkas liikkuu viivalla seuraavan liikeyhtälön mukaan:

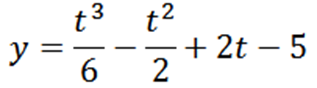
Määritä "t, y" ja "v", kun a = 0.

Tietäen, että nopeus ja kiihtyvyys annetaan

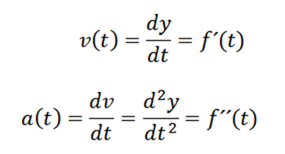
Jatkamme johdettavan ja saamme:

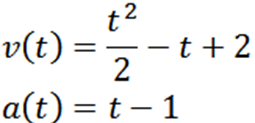
Tekemällä a = 0, meillä on:

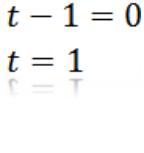
Missä voimme päätellä, että T: n arvo on niin, että a on yhtä suuri kuin nolla on t = 1.

Sitten arvioitaessa t = 1 sijainti- ja funktiotoiminto, meidän on:

Sovellukset

Mplícita -johdannainen

Peräkkäiset johdannaiset voidaan saada myös implisiittisesti johdannaisella.

Esimerkki

Seuraavan ellipsin perusteella etsi "Y":

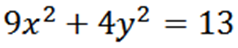
Meillä on epäsuorasti johdettu X: n suhteen: meillä on:

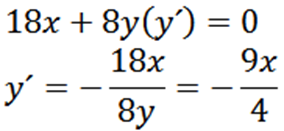
Sitten uudelleen johdetaan epäsuorasti X: n suhteen, antaa meille:

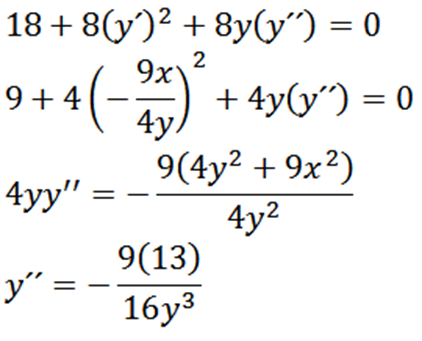
Lopuksi meillä on:

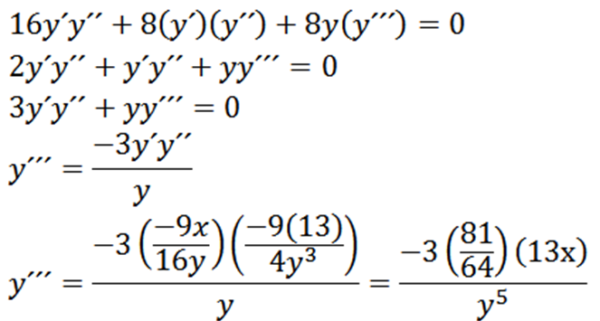
Suhteelliset äärimmäisyydet

Toinen käyttö, jonka voimme antaa toisen järjestyksen johdannaisille, on funktion suhteellisten päiden laskeminen.

Voi palvella sinua: kuinka monta symmetria -akselia ympyrällä on?

Paikallisten ääripäiden ensimmäisen johdannaisen kriteerit kertovat meille, että jos meillä on jatkuva F -funktio aikavälillä (A, B) ja mainitulle aikavälille kuuluu c siten, että se on kumottu C: hen (ts. C, C on kriittinen kohta), yksi näistä kolmesta tapauksesta voi esiintyä:

• Jos f '(x)> 0 jokaiselle X: lle, joka kuuluu (a, c) ja f' (x)<0 para x perteneciente a (c,b), entonces f(c) es un máximo local.
• Jos f '(x) 0 x: lle, joka kuuluu (c, b), niin f (c) on paikallinen minimi.
• Jos f '(x): lla on sama merkki (a, c) ja (c, b), se tarkoittaa, että f (c) ei ole paikallinen pää.

Toisen johdannaisen kriteerien avulla voimme tietää, onko kriittinen määrä funktiota maksimiarvoa vai paikallista minimiä tarvitsematta tehdä se, mikä on funktion merkki edellä mainitulla väliajoilla.

Toisen driftin kriteeri kertoo meille, että jos f '(c) = 0 ja että f "(x) on jatkuvaa kohdassa (a, b), se tapahtuu, jos f" (c)> 0, niin f (c) on a Paikallinen minimi ja jos f "(c) < 0 entonces f(c) es un máximo local.

Jos f "(c) = 0, emme voi päätellä mitään.

Esimerkki

Kun otetaan huomioon funktio f (x) = x⁴ + (4/3) x³ - 4x², Löydä F: n maksimin ja minimin sukulainen soveltamalla toisen johdannaisen kriteerejä.

Ensin lasketaan f '(x) ja f "(x) ja meillä on:

f '(x) = 4x³ + 4x² - 8x

f "(x) = 12x² + 8x - 8

Nyt f '(x) = 0 kyllä, ja vain jos 4x (x + 2) (x - 1) = 0, ja tämä tapahtuu, kun x = 0, x = 1 tai x = - 2.

Sen määrittämiseksi, ovatko saadut kriittiset luvut suhteelliset äärimmäisyydet vain F: ssä "ja tarkkaile siten sen merkkiä.

Voi palvella sinua: Heptagon

f "(0) = - 8, joten f (0) on paikallinen maksimiarvo.

f "(1) = 12, joten f (1) on paikallinen minimi.

f "(- 2) = 24, joten f (- 2) on paikallinen minimi.

Taylor -sarja

Ole f -funktio, joka on määritelty seuraavasti:

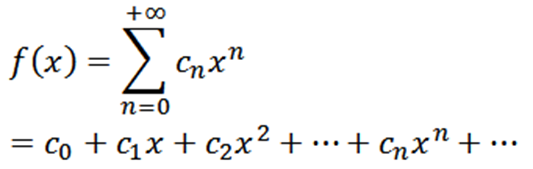
Tällä toiminnolla on lähentymisen säde r> 0 ja se on johdettu kaikista (-r, r) tilauksista. F: n peräkkäiset johdannaiset antavat meille:

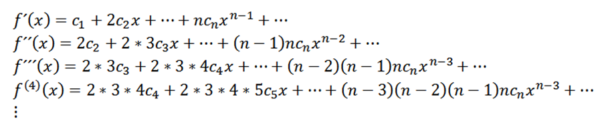
X = 0, voimme saada C: n arvot_n johdannaisista riippuen seuraavasti:

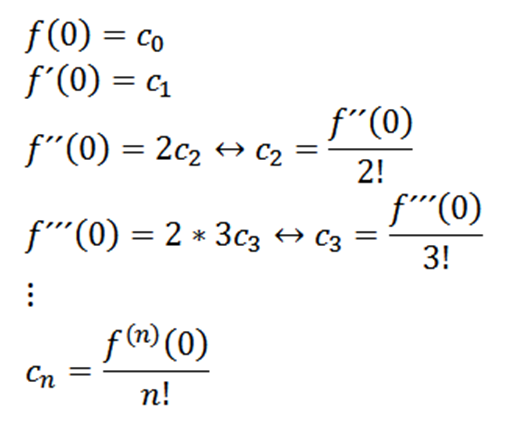
Jos otamme n = 0 funktiona f (ts. F^0 = F), voimme kirjoittaa funktion uudelleen seuraavasti:

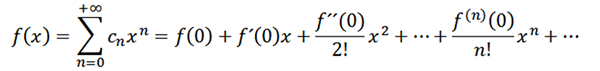
Tarkastellaan nyt funktiota voimien sarjana x = a:

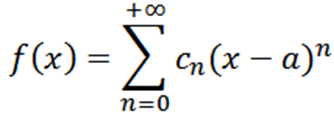
Jos suoritamme analyysin, joka on analoginen edellisen kanssa, meidän on kirjoitettava funktio f seuraavasti:

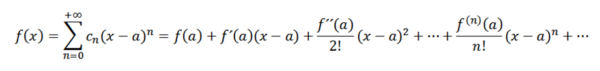
Nämä sarjat tunnetaan nimellä Taylor F sarjassa. Kun a = 0, meillä on erityinen tapaus nimeltään Maclaurin -sarja. Tämäntyyppisillä sarjalla on suuri matemaattinen merkitys etenkin numeerisessa analyysissä, koska näiden ansiosta voimme määritellä toiminnot tietokoneissa, kuten E^x , synti (x) ja cos (x).

Esimerkki

Hanki Maclaurin -sarja E^x.

Huomaa, että jos f (x) = e^x, sitten f^(N)(x) = e^x ja f^(N)(0) = 1, joten Maclaurin -sarjasi on: