Vapaakappalekuva

Mikä on vapaa kehon kaavio?

Eräs Vapaakappalekuva, Eristetty kehon kaavio tai voimakaavio, se on kaavio, jossa ruumiissa toimivat voimat edustavat nuolet.

Sinun on varmistettava, että kaikki esineelle toimivat voimat sisällytetään kaavioon, ja koska se on vektoria, nuoli on vastuussa sen suunnasta ja sen merkityksestä, kun taas sen pituus tarjoaa idean ajatuksen moduuli tai intensiteetti.

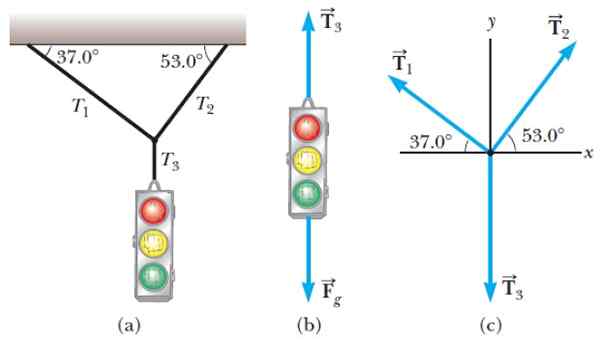
Kuvio 1. a) Kaapeleiden tuesta roikkuva liikennevalo, b) liikennevalon ilmainen runkokaavio ja c) ilmainen runkokaavio kaapelin solmussa. Lähde: Serway, R. Korkeakoulufysiikka.

Kuvassa 1 meillä on esimerkki vapaasta kehon kaaviosta, jota aiomme analysoida.

Tilanne on seuraava: liikennevalo, joka roikkuu muissa kaapeleissa (kuva 1a). Sillä kaksi voimaa toimii, toinen on se, että maa harjoittaa, mikä on paino. Kaaviossa se on merkitty F_g ja toimii pystysuunnassa.

Toinen voima on pystysuoran köyden jännitys, jota kutsutaan T₃ Ja se menee pystysuoraan ylöspäin, pitämällä liikennevaloa ja estämään sitä menemästä maahan.

Kun ongelmassa on useampi kuin yksi esine, on välttämätöntä piirtää kaavio jokaiselle erikseen.

Kaltevien merkkijonojen ja liikennevalon pitävän köyden välistä solmua pidetään tiettynä esineenä ja sen vapaa kehon kaavio on kuvassa 1c. Huomaa, että solmua varten jännitys T₃ on suunnattu alas.

On tärkeää huomata, että vapaassa kehossa kaaviot voimat, joita esine käyttävät muihin kappaleisiin, ei pitäisi ilmestyä, vaan vain niiden, jotka toimivat sen päällä.

Esimerkkejä vapaasta kehon kaaviosta

Vapaa kehon kaavio mahdollistaa Newtonin lakien soveltamisen ja niiden kanssa määrittää liikkeen tila tai muu esine, jolla voimat toimivat. Esitetyn liikennevalon tapauksessa voimme määrittää liikennevalojen alaisten kaapeleiden jännitteiden arvon, joka tunnetaan tämän painon.

Voi palvella sinua: Kuolleet kuormat: Ominaisuudet, laskelmat, esimerkit

Kun nämä tiedot on tiedossa, riittävät kaapelit valitaan ripustamaan liikennevalo ja se täyttää sen toiminnan ilman romahtamista.

Vapaat kehon kaaviot kuvaavat erilaisia ​​päivittäisiä tilanteita, kuten nämä:

Henkilö, joka katselee tavaratilaa tai astiaa

On hyvin yleistä, että ihmisten on siirrettävä raskaita esineitä, kuten kuvion säiliö. Tätä varten heidän on käytettävä voimaa F Säiliössä, joka tässä esimerkissä on vaakasuora ja oikealle, mikä on liikkeen suunta.

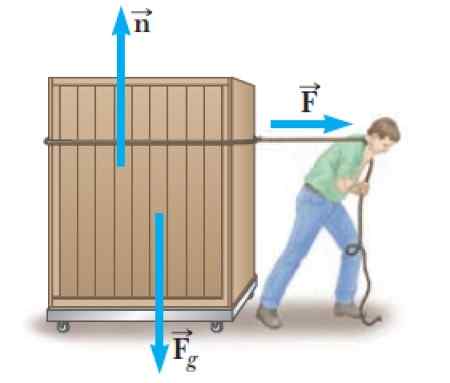Kuva 2. Henkilö käyttää suuruusluokkaa F siirtämään vaakasuoraan raskaan astiaan. Lähde: Serway, R. Korkeakoulufysiikka.

Mutta tämä ei ole ainoa voima, joka toimii häneen, on myös normaalia n, harjoittaa lavan tasaista pintaa pyörillä. Ja lopuksi on sen paino: F_g, Pystysuoraan suuntautuva.

Normaali on voima, joka syntyy niin kauan kuin kaksi pintaa on kosketuksessa ja on aina kohtisuorassa sitä käyttävään pintaan nähden. Tässä tapauksessa pyöränlustalla on normaali astiassa.

Lohko, joka liukuu kaltevan tason läpi

Joillakin työpöydällä on hiukan kalteva taulukko, jotta muistiinpanot olisivat mukavampia ja luettavia. Siinä on myös A-Lapiz-paikka, mutta olemme kaikki laittaneet kynän pöydälle paikasta ja olemme nähneet kuinka se liukuu pöydälle.

Mitkä joukot toimivat lyijykynällä?

Sama, joka toimii seuraavassa vapaassa rungon kaaviossa esitetyssä lohkossa:

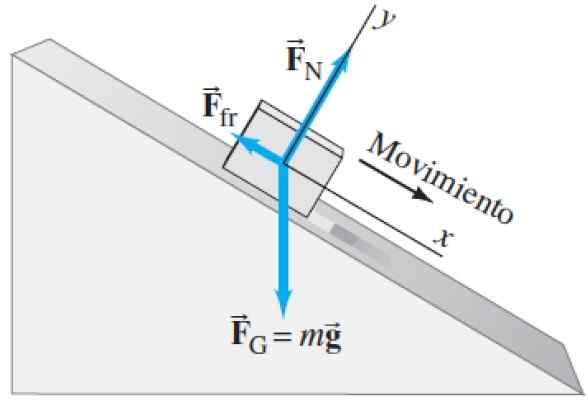Kuva 3.- Kohteen (lohko tai lyijykynä), joka liukuu kaltevalle tasolle kitkalla, on vapaa kehon kaavio. Lähde: Giancoli, D. Fysiikka: sovellusten periaatteet.

Normaali F_N Se on voima, jota pöydän pinta käyttää lyijykynään tai tuetulle lohkolle. Toisin kuin edellisessä esimerkissä, normaali ei ole pystysuora, vaan kalteva. Muista, että normaali on lohkon taulukon kohdistama voima ja se on kohtisuorassa siihen. Kun taulukko on kalteva, myös normaali.

Se voi palvella sinua: Ensimmäinen tasapainotila: Selitys, esimerkit, harjoitukset

Kuten aina paino F_g Se on pystysuora, välinpitämätön järjestelmän kaltevuudesta.

Ja lopuksi meillä on uusi voima, joka on kineettinen kitka F_fr Taulukon ja lyijykynän tai lohkon välillä. Kitka on myös kosketusvoima, mutta toisin kuin normaali, se on tangentiaalinen (yhdensuuntainen) voima pintaan. Huomaa myös, että se on aina suunnattu liikkeen vastaisesti.

Atwood -kone

Atwood -kone on yksinkertainen kone, joka koostuu kevyestä hihnapyörästä ja ilman kitkaa kiskossa, jonka läpi kevyt ja vaikuttamaton köysi kulkee.

Kaksi massaobjektia ripustetaan samasta₁ ja m₂. Kun yksi esineistä nousee, toinen laskeutuu, kuten kuvassa 4 esitetään:

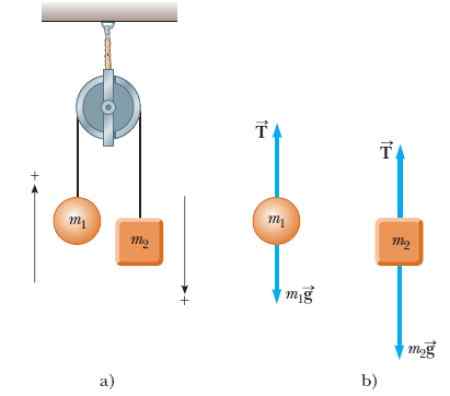Kuva 4. Atwood -kone ja köydestä roikkuvien massojen vastaavat vapaat rungon kaaviot. Lähde: Serway, R. Korkeakoulufysiikka.

Koska esineitä on kaksi, vapaa kehon kaavio tehdään erikseen. Molemmille esineille on vain kaksi voimaa: köyden jännitys T ja vastaavat painot.

Kuvassa jokainen paino ilmaistaan ​​suoraan massan tuloksena kiihtyvyydellä. Sen puolestaan ​​jännitys on aina suunnattu pystysuoraan jännitystä pitkin.

Liikuntaa

Käytä Newtonin lakeja määrittääksesi kiihtyvyyden, jonka kanssa edellisessä osiossa esitetyn Atwood -koneen massat.

Ratkaisu

Newtonin toisessa laissa todetaan, että voimien summa on yhtä suuri kuin massan tuote kiihtyvyydellä.

Kummankin massan merkintökokous voi olla erilainen, joten pidämme positiivisena merkityksenä, että liikkeen, kuten kuvaajan, ensimmäinen massa nousee ja toinen laskeutuu.

Se voi palvella sinua: pinnalliset aallot: ominaisuudet, tyypit ja esimerkit

Joissakin ongelmissa lausunto ei anna tietoa, niin merkintöjen on.

-Massalle 1 (lataus):

T - m₁g = m₁-lla

-Massalle 2 (matala):

-T + m₂g = m₂-lla

Molemmat yhtälöt muodostavat kahden tuntemattoman lineaarisen yhtälöjärjestelmän, koska jännite näkyy erilaisella merkinnällä jokaisessa yhtälössä, lisäämme ne vain termiin ja jännitys peruutetaan:

m₂G - m₁g = m₁A + M₂-lla

a = m₂G - m₁G / (m₁ + m₂-A

Viitteet

1. Bauer, W. 2011. Fysiikka tekniikkaan ja tieteisiin. Osa 1. MC Graw Hill.
2. Giancoli, D.  2006. Fysiikka: sovellusten periaatteet. Kuudes. Ed Prentice Hall.
3. Serway, R., ULOLE, c. 2011. Korkeakoulufysiikka. 9na ed. Cengage -oppiminen.
4. Tipler, P. (2006) Tieteen ja tekniikan fysiikka. 5. ed. Osa 1. Toimitus palautti.
5. Tippens, P. 2011. Fysiikka: Käsitteet ja sovellukset. 7. painos. McGraw Hill