Kaavojen, yhtälöiden, esimerkkien, harjoitusten ero

Se Kuutioerot Se on muodon binomiaalinen algebrallinen ekspressio³ - b -³, missä termit A ja B voivat olla todellisia lukuja tai erityyppisiä algebrallisia lausekkeita. Esimerkki kuutioeristä on: 8 - x³, Koska 8 voidaan kirjoittaa 2³.

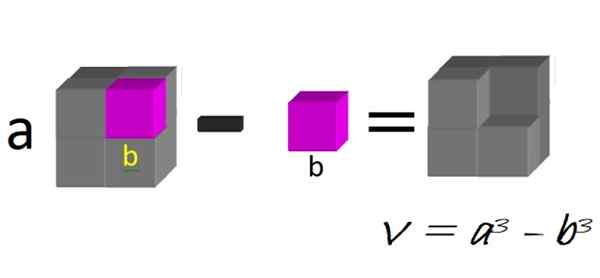
Geometrisesti voimme ajatella suurta kuutiota, sivulta A, johon sivun B -pienen pykälän vähennetään, kuten kuvassa 1 esitetään:

Kuvio 1. Kuutioiden ero. Lähde: f. Zapata.

Tuloksena olevan kuvan tilavuus on tarkalleen ero kuutioissa:

V = a³ - b -³

Vaihtoehtoisen ekspression löytämiseksi havaitaan, että tämä luku voidaan jakaa kolmeen prismaan, kuten alla on esitetty:

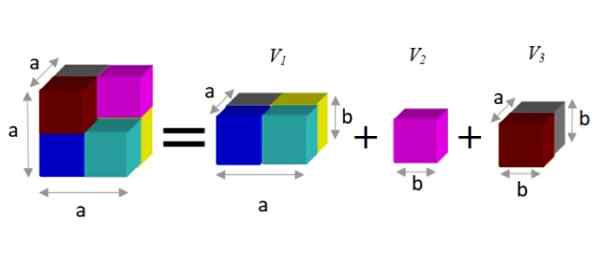Kuva 2. Kuutioiden ero (tasa -arvon vasen) on yhtä suuri kuin osittaisten tilavuuksien summa (oikea). Lähde: f. Zapata.

Prismalla on kolmen ulottuvuuden tuote antaa tilavuus: Leveys x korkea x syvyys. Tällä tavoin tuloksena oleva tilavuus on:

V = a³ - b -³ = a².B + B³ + -lla.b -²

Tekijä b - Se on yhteinen oikealle. Lisäksi yllä esitetyssä kuvassa se täyttyy erityisesti, että:

b = (a/2) ⇒ a = b + b

Siksi voidaan sanoa, että: b = a - b. Täten:

-lla³ - b -³ = B (a² + b -² +-lla.b) = (a-b) (a² + -lla.B + B²-A

Tämä tapa ilmaista ero kuutioissa osoittautuu erittäin hyödylliseksi monissa sovelluksissa ja se olisi saatu samalla tavalla, vaikka puuttuva kuutiopuoli nurkassa oli erilainen kuin b = A/2.

Huomaa, että toinen suluSe näyttää paljon summan neliön huomattavalta tuotteesta, mutta ylitetty termi ei kerrotaan 2: lla. Lukija voi kehittää oikean puolen varmistaakseen, että se on tehokkaasti -lla³ - b -³.

[TOC]

Voi palvella sinua: neliömäinen binomi

Esimerkit

Kuutioita on useita: eroja:

1 - m⁶

-lla⁶b -³ - 8z¹²ja⁶

(1/125).x⁶ - 27.ja⁹

Analyysi jokainen heistä. Ensimmäisessä esimerkissä 1 voidaan kirjoittaa 1 = 1³ ja termi m⁶ Se pysyy: (M²-A³. Molemmat termit ovat täydellisiä kuutioita, joten niiden ero on:

1 -m⁶ = 1³ - (m²-A³

Toisessa esimerkissä termit kirjoitetaan uudelleen:

-lla⁶b -³ = (a²b)³

8z¹²ja⁶ = 2³ (z⁴-A³ (ja²-A³ = (2z⁴ja²-A³

Näiden kuutioiden ero on: (a²b)³ - (2Z⁴ja²-A³.

Lopuksi murto (1/125) on (1/5³), x⁶ = (x²-A³, 27 = 3³ ja ja⁹ = (ja³-A³. Korvaamalla kaiken tämän alkuperäisessä lausekkeessa, se saadaan:

(1/125).x⁶  - 27y⁹ = [(1/5) (x²)³ - (3y³-A³

Kuutioerot tekijä

Tosiasia kuutioissa yksinkertaistaa monia algebrallisia operaatioita. Tätä varten riittää käyttämään aiemmin vähennettyä kaavaa:

Kuva 3. Kuutioerojen tekijä ja huomattavan osamäärän ekspressio. Lähde: f. Zapata.

Nyt tämän kaavan soveltamismenettely koostuu kolmesta vaiheesta:

- Ensinnäkin saadaan kunkin eron termin kuutiometriä.

- Sitten kaavan oikealla puolella näkyvät binomit ja trinomit on rakennettu.

- Lopuksi binomiaalinen ja trinomiaalinen korvataan lopullisen tekijän saamiseksi.

Havainnollamme näiden vaiheiden käyttöä jokaisessa esimerkissä edellä ehdotetuista kuutioeroista ja siten saamme sen tekijän ekvivalentin.

Esimerkki 1

Tosiasiallinen ilmaisu 1 -m⁶   Kuvattujen vaiheiden seuraaminen. Aloitamme kirjoittamalla lauseke 1 -m⁶ = 1³ - (m²-A³ Kunkin termin vastaavien kuutiomuotojen purkamiseksi:

Sitten rakennetaan binomiaalinen ja trinomiaalinen:

Se voi palvella sinua: jonoteoria: historia, malli, mihin se on ja esimerkkejä

A = 1

b = m²

Niin:

A - b = 1 - m²

 (² +-lla.B + B²) = 1² + 1.m² + (m²-A² = 1 + m² + m⁴

 Lopuksi se korvataan kaavassa A³ - b -³ = (a-b) (a² +-lla.B + B²)

1 -m⁶ = (1 - m²) (1 + m² + m⁴-A

Esimerkki 2

Vaikuttakaa:

-lla⁶b -³ -8z¹²ja⁶ = (a²b)³ - (2Z⁴ja²-A³

Koska nämä ovat täydellisiä kuutioita, kuutiomuodot ovat välittömiä: a²B ja 2Z⁴ja², Sieltä seuraa, että:

- Binomial: a²B - 2Z⁴ja²

- Trinomial: (a²b)² + -lla²b -. 2Z⁴ja² + (²B +2Z⁴ja²-A²

 Ja nyt haluttu tekijä on rakennettu:

-lla⁶b -³ -8z¹²ja⁶ = (a²B - 2Z⁴ja²-A. [(²b)² + -lla²b -. 2Z⁴ja² + (²B + 2Z⁴ja²-A²] =

= (a²B - 2Z⁴ja²-A. [⁴b -² + Toinen²b -.z -z⁴ja² + (²B + 2Z⁴ja²-A²-

Periaatteessa tekijä on valmis, mutta jokaista termiä on usein tarpeen yksinkertaistaa. Sitten huomattava tuote kehitetään summasta - joka ilmestyy lopussa ja lisää sitten samanlaisia ​​termejä. Muistatko, että summan neliö on:

(x + y)² = x² + 2xy + ja²

Merkittävä oikeus oikealle kehittyy tällä tavalla:

(²B + 2Z⁴ja²-A² = a⁴b -² + Neljäs²b -.z -z⁴ja² + 4Z⁸ja⁴

 Kuutioiden eron tekijän tekijän tekijän korvaaminen:

-lla⁶b -³ -8z¹²ja⁶ = (a²B - 2Z⁴ja²-A. [⁴b -² + Toinen²b -.z -z⁴ja² + -lla⁴b -² + Neljäs²b -.z -z⁴ja² + 4Z⁸ja⁴] =

Lopuksi, samanlaisten termien ryhmittely ja numeeriset kertoimet, jotka ovat kaikki pareja, on saatu:

(²B - 2Z⁴ja²-A. [Toinen⁴b -² + Kuudes²b -.z -z⁴ja² + 4Z⁸ja⁴] = 2 (a²B - 2Z⁴ja²-A. [⁴b -² + Kolmas²b -.z -z⁴ja² + 2Z⁸ja⁴-

Esimerkki 3

Tekijä (1/125).x⁶  - 27y⁹ Se on paljon yksinkertaisempi kuin edellinen tapaus. Ensinnäkin tunnistetaan a ja b ekvivalentit:

A = (1/5) x²

B = 3y³

Sitten ne korvataan suoraan kaavassa:

(1/125).x⁶  - 27y⁹ = [(1/5) x² - 3y³-. [(1/25) x⁴ + (3/5) x²ja³ + 9y⁶-

Liikuntaa

Kuutioiden ero on, kuten olemme sanoneet, erilaisia ​​sovelluksia algebrassa. Katsotaanpa joitain:

Voi palvella sinua: 5 Cartesian -lentokoneen ominaisuutta

Harjoitus 1

Ratkaise seuraavat yhtälöt:

a) x⁵ - 125 x² = 0

b) 64 - 729 x³ = 0

Liittää jhk

Ensinnäkin yhtälö on tekijä tällä tavalla:

x² (x³ - 125) = 0

Koska 125 on täydellinen kuutio, sulku on kirjoitettu erona kuutioissa:

x² . (x³ - 5³) = 0

Ensimmäinen ratkaisu on x = 0, mutta löydämme lisää, jos teemme x³ - 5³ = 0, sitten:

x³ = 5³ → x = 5

Ratkaisu b

Yhtälön vasen puoli kirjoitetaan uudelleen 64 - 729 x³ = 4³ - (9x)³. Siksi:

4³ - (9x)³ = 0

Koska eksponentti on sama:

9x = 4 → x = 9/4

Harjoitus 2

Vaikuta ekspressio:

(x + y)³ - (X - y)³

Ratkaisu

Tämä lauseke on ero kuutioissa, jos huomamme tekijä kaavassa, että:

A = x+ ja

b = x- y

Sitten binomi rakennetaan ensin:

a - b = x+ y - (x- y) = 2y

Ja nyt trinomiaalinen:

-lla² + -lla.B + B² = (x+ y)² + (x + y) (x-y) + (x-y)²

Kehitetään merkittäviä tuotteita:

(x+ y)² = x² + 2xy +ja²

(x+y) (x-y) = x²- ja²

(x- y)² = x² - 2xy +ja²

Sitten sinun on korvattava ja vähennettävä samanlaisia ​​termejä:

-lla² + -lla.B + B² = x² + 2xy +ja²+ x²- ja²+ x² - 2xy +ja² = 3x² + ja²

Tekijä johtaa:

(x + y)³ - (X - y)³ = 2y. (3x² + ja²-A

Viitteet

1. Baldor, a. 1974. Algebra. Venezuelan kulttuuritoimitus S.-Lla.
2. CK-12-säätiö. Kuutioiden summa ja ero. Toipunut: CK12.org.
3. Khan -akatemia. Kuutiot erotekijä. Palautettu: on.Khanacademy.org.
4. Matematiikka on hauskaa edistynyttä. Kahden kuutio ero. Toipunut: MathSisfun.com
5. Yksinäinen. Kuutioerot tekijä. Haettu: DCB.Fi-c.Yksinäinen.MX.