Fyysinen osoite)
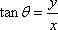
- 1646
- 38
- Ronald Reilly
Mikä on osoite?
Se Fysiikan hallinta Se on vakiintunut viiva, joka kulkee kehon tai esineen läpi, kun he tekevät liikkeen. Suunta on erittäin tärkeä erityisesti mekaniikan kokeissa, koska siinä tutkitaan kehon liikettä ja missä se liikkuu (ottaen huomioon väliaikainen muuttuja).
Fysiikan kentällä suunta on osa liikkeen elementtejä, koska se edustaa linjaa, jolla liikkuva esine tai runko lepää.
Kehon suunta voi vaihdella vasemmalta oikealle, oikealta vasemmalle, ylhäältä alas tai päinvastoin. Jos piirrämme ylöspäin nuolen, sanomme, että sen suunnan kulma on 90 ° lähtökohtaan nähden.
Osoite ja vektorit
Kuten aiemmin mainittiin, osoite liittyy tiukasti liikkeeseen ja voimme löytää sen elementiä, joka tunnetaan nimellä siirtymävektori.
Osoite on osa vektoreita, ja siksi on tarpeen tietää tarkalleen mitä he ovat ja miten ne toimivat. On yleistä sekoittaa vektorin suunta tämän merkitykseen. Osoite on yksinkertaisesti tapa ottaa vektorilta ja merkitys on siellä, missä se on suunnattu.
Selkeämpi esimerkki tästä olisi:
Jos juna menee oikealle kiskolle, se olisi sinun osoitteesi.
Toisaalta, jos juna päättää mennä eteenpäin tai taaksepäin samassa kiskossa, sitä pidetään saman merkityksenä.
Vektori on suuruus vertailujärjestelmässä, joka koostuu moduulista ja osoitteesta.
Voi palvella sinua: Aerostaattinen ilmapallo: Historia, ominaisuudet, osat, miten se toimiiVektorit voidaan kohdistaa kardinaalipisteisiin, kuten pohjoiseen, etelään, itään ja länteen (muodostaen eräänlaisen ristin), mutta samalla on mahdollista, että vektorin suunta on suunnattu koilliseen (diagonaalinen viiva).
Vektorien suunnan ominaisuudet
Vektorin suunta voidaan määritellä myös viivalla tai mikä tahansa vektoriin sisältävä rinnakkaisviiva. Vektorin suunnassa on 2 perusominaisuutta:
- Vektorien suunta mitataan alkuperäisestä pisteestä kardinaalipisteisiin ja sen mittaus voidaan ilmaista kulmajärjestelmän avulla.
- Vektoreiden suunta lasketaan vastakkaiseen suuntaan kuin lähtökohdasta lähtökohdasta kardinaalipisteisiin. Esimerkki tästä olisi, jos vektori rikki 30 °. Sitten 30 ° kelloneulojen vastakkaiseen suuntaan on siirretty.
Yhtälöt vektorin suunnan löytämiseksi
On monia tapoja laskea suunta, johon vektori on suunnattu. Alla on kaksi yleisintä fyysisissä kokeissa:
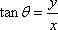
, missä x on vaakasuuntainen muutos e y on pystysuuntainen muutos.
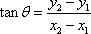
, Missä (x 1 ja 1) on alkupiste y (x 2 ja 2) on päätepiste.
Yhteenvetona voidaan todeta.
Viitteet
- Vektorin suuruus ja suunta. Toipunut www.Matematiikanhuone.com
- Suunta ja laakerivektori. Toipunut www.Ongelmat.com

