Euklidian etäisyyskonsepti, kaava, laskenta, esimerkki

Se Euklidian etäisyys Se on positiivinen luku, joka osoittaa erottelun, joka kahdella pisteellä on tilassa, jossa euklidigeometrian aksioomit ja lauseet täyttyvät.

Euklidian tilan kahden pisteen A ja B välinen etäisyys on vektorin pituus Ab Kuuluu ainoaan linjaan, joka kulkee näiden pisteiden läpi.

Kuvio 1 . Yksidimensionaalinen euklidinen tila, jonka on muodostettu linjalla (OX). Useita pisteitä tässä tilassa, niiden koordinaatit ja etäisyydet on esitetty. (Valmistaja Ricardo Pérez).

Tila, jonka havaitsemme ja jossa liikutamme ihmisiä. Tässä tilassa ovat kahden dimensionaaliset alaosat (suunnitelmat) ja yhden dimensionaaliset (suora) (suora) alaosat.

Euklidiset tilat voivat olla yhden ulottuvuuden (1-D), kaksiulotteisia (2-D), kolmiulotteita (3-D) tai N-ulottuvuuksia (N-D).

Nämä ovat pisteitä yhden ulottuvuuden avaruudessa X, jotka kuuluvat suuntautuneeseen viivaan (OX), suunta X: stä X on positiivinen osoite. Pisteiden löytämiseksi tällä linjalla Cartesian järjestelmää, joka koostuu linjan jokaisen pisteen osoittamisesta, käytetään numeroa.

[TOC]

Kaava

Euklidian etäisyys D (A, B) on määritelty pisteiden A ja B välillä, jotka sijaitsevat linjalla, kuten sen X -koordinaattien erojen neliön neliöjuuri:

D (a, b) = √ ((xb - xa)^2)

Tämä määritelmä takaa, että: kahden pisteen välinen etäisyys on aina positiivinen määrä. Ja että etäisyys A: n ja B: n välillä on yhtä suuri kuin etäisyys B: n ja a: n välillä.

Kuvio 1 esittää yhden dimensionaalisen euklidian tilan, jonka linja (OX) on muodostettu ja useita pisteitä kyseisellä linjalla. Jokaisella pisteellä on koordinaatti:

Kohta A on XA -koordinaatti = 2.5, B -koordinaatti XB = 4 ja piste C -koordinaatti XC = -2.5

Se voi palvella sinua: Taajuuden todennäköisyys: Konsepti, miten se lasketaan ja esimerkkejä

D (a, b) = √ ((4 - 2.5) 2) = 1.5

D (b, a) = √ ((2.5 - 4) 2) = 1.5

D (a, c) = √ (-2.5 - 2.5) 2) = 5.0 -

Euklidian etäisyys kahdessa ulottuvuudessa

Kaksi dimensionaalista eukliditila on taso. Esimerkiksi euklidian tason kohdat kohtaavat euklidigeometrian aksioomit:

- Kahdessa pisteessä yksi rivi kulkee. 

- Kolme pistettä tasossa muodostavat kolmion, jonka sisäkulmat lisäävät aina 180º.

- Suorakulmiokolmiossa hypotenuusin neliö on yhtä suuri kuin jalkojen neliöiden summa.

Kahdessa ulottuvuudessa pisteellä on X- ja Y -koordinaatit. 

Esimerkiksi pisteessä P on koordinaatit (XP, YP) ​​ja piste, joka koordinoi (xq, yq).

Euklidinen etäisyys pisteen P ja Q välillä määritetään seuraavalla kaavalla:

D (p, q) = √ ((xq - xp)^2 + (yq - yp)^2)

On huomattava, että tämä kaava vastaa Pythagoras -lausetta, kuten kuvassa 2 esitetään.

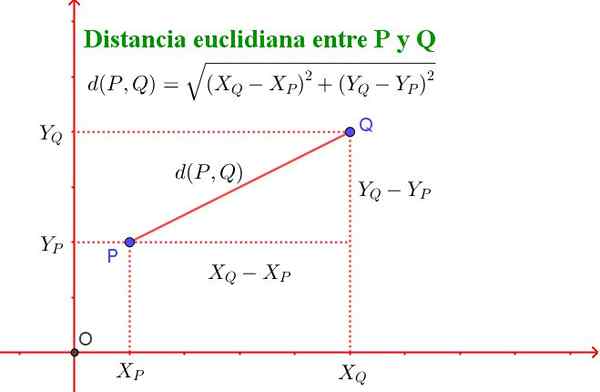Kuva 2. Kahden pisteen P ja Q: n välinen etäisyys kohtaa Pythagoras -lauseen. (Valmistaja Ricardo Pérez).

Ei -uclidian pinnat

Kaikki kaksi dimensionaalista tilaa eivät täytä euklidista geometriaa. Pallon pinta on kaksiulotteinen tila.

Pallomaisen pinnan kolmion kulmat eivät lisää 180º: ta, ja tällä pythagoras -lause ei täyty, joten pallomainen pinta ei täytä euklidin aksioomia.

Euklidian etäisyys N -ulottuvuuksissa

Koordinaattien käsite voidaan laajentaa suurempiin ulottuvuuksiin:

- 2-D-pisteessä P on koordinaatit (XP, YP)

- 3D-pisteessä, jolla on koordinaatit (xq, yq, zq)

- 4-D-pisteessä R on koordinaatit (XR, YR, ZR, WR)

- N-D-pisteessä P on koordinaatit (P1, P2, P3, ..., PN)

Voi palvella sinua: Baarien kuvaaja: Ominaisuudet, mitä se on, esimerkkejä

N-ulotteisen euklidialaisen tilan kahden p- ja q-pisteen välinen etäisyys lasketaan seuraavalla kaavalla:

D (p, q) = √ ((q1 - p1)^2 +(q2 - p2)^2 +… +(qn - pn)^2)

Kaikkien pisteiden geometrinen paikka, että n-ulotteisessa euklidisessa tilassa, joka toisesta kiinteästä P-pisteestä (keskuksesta) muodostavat n-ulotteisen hypersferan.

Kuinka laskea euklidian etäisyys

Alla on etäisyys kahden euklidian kolmiulotteisessa tilassa, joka on laskettu.

Oletetaan, että Cartesian -koordinaatit x, y, z on antanut :( 2, 3, 1) ja koordinaattien kohta B :( -3, 2, 2).

Haluat määrittää näiden pisteiden välisen etäisyyden, jota varten yleistä suhdetta käytetään:

D (a, b) = √ ((-3 - 2) 2 + (2 - 3) 2 + (2 - 1) 2) = √ ((-5) 2 + (-1) 2 + (1) 2 -A

D (a, b) = √ (25 + 1 + 1) = √ (27) = √ (9 *3) = 3 √ (3) = 5,196

Esimerkki

On kaksi pistettä P ja Q.  Piste Cartesian -koordinaateille x, y, z, joka on annettu p :( 2, 3, 1) ja koordinaattien pisteen Q :( -3, 2, 1).

[PQ] -segmentin keskipisteen M koordinaatit pyydetään löytävän kaksi pistettä yhdistävät koordinaatit. 

Ratkaisu:

Oletetaan, että tuntemattomalla pisteellä M on koordinaatit (x, y, z).

Koska m on [pq]: n keskimääräinen piste, on täytettävä, että d (p, m) = d (q, m), joten se on myös täytettävä d (p, m)^2 = d (q, m)^ 2:

(X - 2)^2 + (y - 3)^2 + (z - 1)^2 = (x - (-3))^2 + (y - 2)^2 + (z - 1)^2

Kuten tässä tapauksessa, kolmas termi on sama kahdessa jäsenessä, edellistä lauseketta yksinkertaistetaan:

Voi palvella sinua: Absoluuttinen vakio

(X - 2)^2 + (y - 3)^2 = (x + 3)^2 + (y - 2)^2 

Sitten on yhtälö kahdella tuntemattomalla x ja y. Toinen yhtälö tarvitaan ongelman ratkaisemiseksi.

Piste M kuuluu linjaan, joka kulkee P- ja Q -pisteiden läpi, jotka voimme laskea seuraavasti:

Ensimmäinen on johtajavektori Pq linja: Pq = = .

Sitten P = Oppi + -lla Pq, missä Oppi Se on pisteen p ja vektoriasento ja -lla Se on parametri, joka kuuluu reaalilukuihin. 

Aikaisempi yhtälö tunnetaan linjan vektoriyhtälöksi, joka Cartesian koordinaateissa hyväksyy seuraavasti:

= + a =

Yhtä suuret vastaavat komponentit ovat:

X - 2 = 2 - 5 A; Ja - 3 = 3 -a; Z - 1 = 0

Toisin sanoen x = 4 - 5a, y = 6 - a, lopulta z = 1.

Se korvataan kvadraattisessa lausekkeessa, joka yhdistää x: n y:

(4 - 5A - 2)^2 + (6 - A - 3)^2 = (4 - 5A + 3)^2 + (6 - A - 2)^2

Sitä yksinkertaistetaan:

(2 - 5a)^2 + (3 -a)^2 = (7 - 5a)^2 + (4 - a)^2

Nyt kehittää:

4 + 25 a^2 - 20a + 9 + a^2 - 6a = 49 + 25 a^2 - 70a + 16 + a^2 - 8a

Sitä yksinkertaistetaan, peruuttaa samanlaiset ehdot molemmissa jäsenissä:

4 - 20a + 9 - 6a = 49 - 70a + 16 - 8a

Parametri A:

52 a = 49 + 16 - 4 - 9 = 52, mikä johtaa A = 1.

Toisin sanoen x = 4 - 5, y = 6 - 1, lopulta z = 1.

Lopuksi hankimme segmentin [pq] Cartesian koordinaatit:

M: (-1, 5, 1).

Viitteet

1. Lehmann C. (1972) Analyyttinen geometria. Uteha.
2. Superprof. Kahden pisteen välinen etäisyys. Toipunut: SuperProf.On
3. Yksinäinen. Etäisyys sublineaaristen lajikkeiden välillä. Toipunut: Prometheus.Matem.Yksinäinen.MX/
4. Wikipedia. Euklidian etäisyys. Palautettu: on.Wikipedia.com
5. Wikipedia. Euklidinen tila. Palautettu: on.Wikipedia.com