Synteettinen jako

Selitämme, mikä synteettinen jako on, menetelmä sen tekemiseen, esimerkkejä ja harjoituksia ratkaistu.

Mikä on synteettinen jako?

Se Synteettinen jako Se on yksinkertainen tapa jakaa polynomi p (x) yhdellä muodosta d (x) = x - c - c. Esimerkiksi polynomi p (x) = (x⁵+3x⁴-7x³+2x²-8x+1) Se voidaan esittää kahden yksinkertaisimman polynomin (x+1) ja (x kertolaskuna (x⁴ + 2x³-A.

Se on erittäin hyödyllinen työkalu, koska sen lisäksi, että voimme jakaa polynomit, se mahdollistaa myös P (x) -polynomin arvioinnin missä tahansa numerossa C, mikä puolestaan ​​osoittaa meille tarkasti, jos tämä luku on nolla vai ei polynomi-.

Jakoalgoritmin ansiosta tiedämme, että jos meillä on kaksi p (x) ja d (x) polynomi (x) + r (x), missä r (x) on nolla tai on pienempi kuin q (x). Nämä polynomit tunnetaan osamääräksi ja jäännöksi tai lepo.

Toisinaan, joissa polynomi d (x) on x - c -muodossa, synteettinen jako antaa meille lyhyen tavan löytää kuka on q (x) ja r (x).

Synteettinen jakautumismenetelmä

Olkoon p (x) = a_nxⁿ+-lla_N-1x^N-1+… +A₁x+a_{0 -} Polynomi, jonka haluamme jakaa ja d (x) = x-c jakaja. Jakoon synteettisellä jakautumismenetelmällä jatkamme seuraavasti:

1- Kirjoitamme p (x) -kertoimet ensimmäisessä rivissä. Jos X -virtaa ei ilmesty, asetamme nollan sen kertoimeksi.

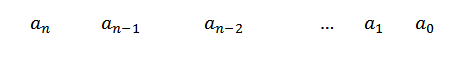
2- toisessa rivissä, a: n vasemmalla puolella_n Sijoitamme C ja piirtämme jakoviivat, kuten seuraavassa kuvassa on esitetty:

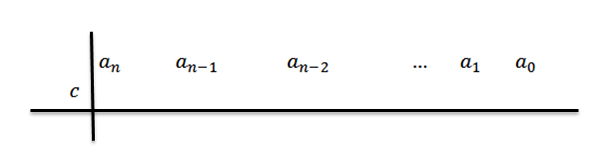
3- Alennamme johtava kertoimen kolmanteen riviin.

Voi palvella sinua: Euler -menetelmä: Mikä on menettelyn ja harjoitusten käyttö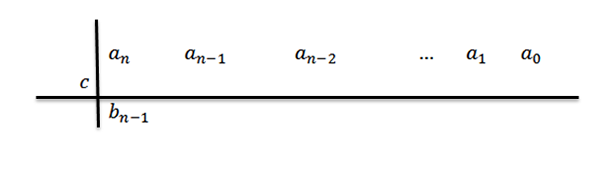

Tässä lausekkeessa b_N-1= a_n

4- Kerroin C: llä johtavalla kertoimella B_N-1 Ja kirjoitamme tulos toisessa rivissä, mutta oikealla oleva sarake.

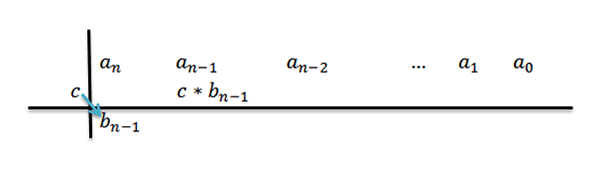
5- Lisäämme sarakkeen, johon kirjoitamme edellisen tuloksen ja tulos on sijoitettu mainitulle summalle. Eli samassa sarakkeessa kolmas rivi.

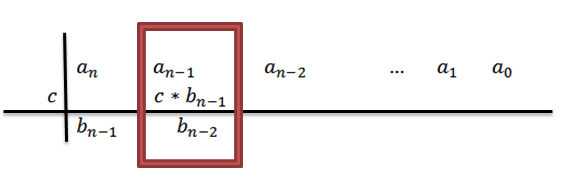
Lisäämällä, meillä on seurauksena_N-1+c*b_N-1, Mihin mukavuuteen soitamme b_N-2

6- Kerroin c edellisellä tuloksella ja kirjoitamme tulos oikealle toiselle riville.

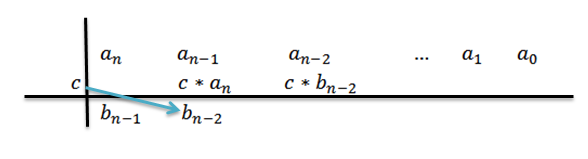
7- Toistamme vaihe 5 ja 6, kunnes saavutamme kerroimen_{0 -}.

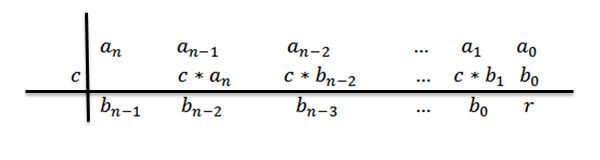
8- Kirjoitamme vastauksen, toisin sanoen jako ja jäännös. Kun teemme luokan N polynomin jakautumisen luokan 1 polynomin välillä, meillä on, että osuus olisi luokka N-1.

Jakojen polynomin kertoimet ovat kolmannen rivin numerot, paitsi viimeinen, joka on jäännöspolynomi tai muu jako.

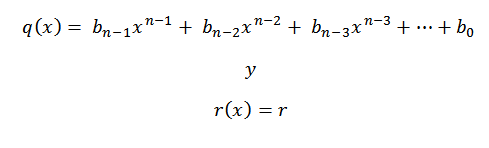
Ratkaisut

Esimerkki 1

Tee seuraava jako synteettisellä jakautumismenetelmällä:

(x⁵+3x⁴-7x³+2x²-8x+1): (x+1).

Ratkaisu

Ensin kirjoitamme osinkokertoimet seuraavasti:

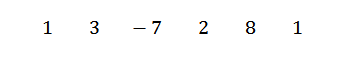
Sitten kirjoitamme C: n vasemmalla puolella, toisella rivillä, jakoviivojen kanssa. Tässä esimerkissä c = -1.

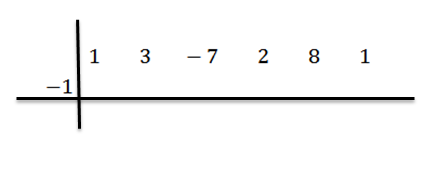
Laskemme johtavaa kertoimia (tässä tapauksessa B_N-1 = 1) ja me kertomme sen -1: n:

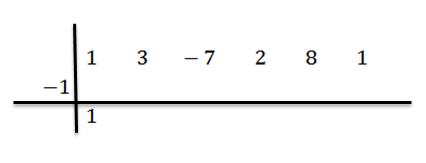
Kirjoitimme sen tuloksen oikealle toiselle riville, kuten alla on esitetty:

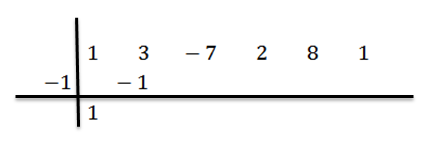
Lisäämme toisen sarakkeen numerot:

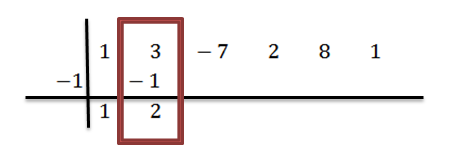
Kerrotaan 2: lla -1 ja kirjoitamme tulos kolmanteen sarakkeeseen, toiseen riviin:

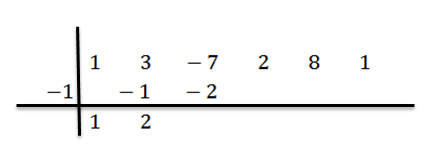
Lisäämme kolmanteen sarakkeeseen:

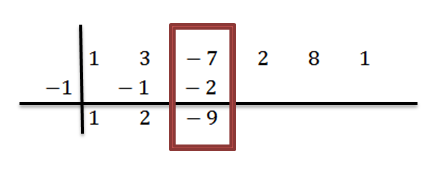
Jatkamme analogisesti, kunnes saavutamme viimeisen sarakkeen:

Voi palvella sinua: oletus ja ylimääräinen lähestymistapa: Mikä on ja esimerkkejä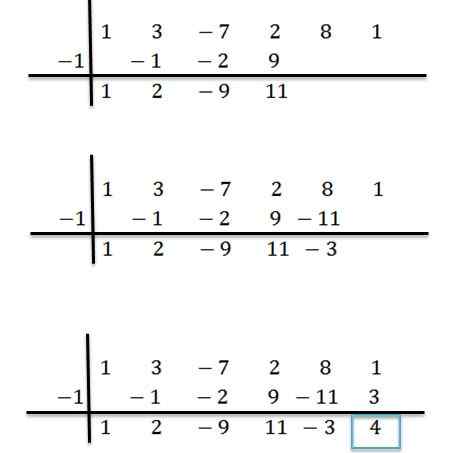

Siten meillä on, että viimeinen saatu numero on muu jako, ja jäljellä olevat numerot ovat osamäärän polynomin kertoimet. Tämä on kirjoitettu seuraavasti:

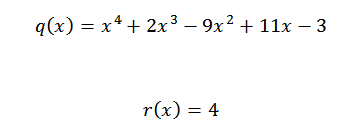
Jos haluamme varmistaa, että tulos on oikea, riittää varmistamaan, että seuraava yhtälö täyttyy:

P (x) = q (x)*d (x) + r (x)

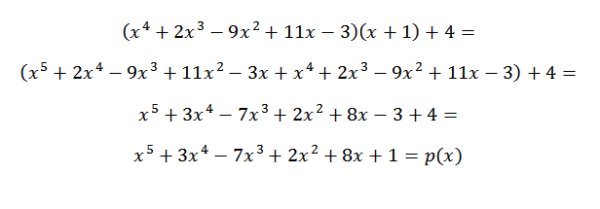
Siksi voimme varmistaa, että saatu tulos on oikea.

Esimerkki 2

Suorita seuraava polynominen jako synteettisellä jakautumismenetelmällä:

(7x³-x+2): (x+2)

Ratkaisu

Tässä tapauksessa meillä on termi x² Se ei ilmesty, joten kirjoitamme arvoon 0 kerroin. Siten polynomi pysyisi 7x³+0x²-x+2.

Kirjoitamme kertoimet peräkkäin, eli:

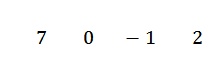
Kirjoitamme arvon c = -2 toiselle riville vasemmalle puolelle ja piirtämme jakoviivat.

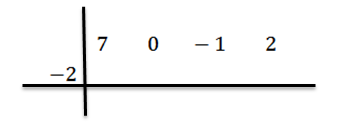
Laskemme johtavan kerroin B_N-1 = 7 ja me kertomme sen -2: lla kirjoittamalla sen tuloksen toiseen riviin oikealle.

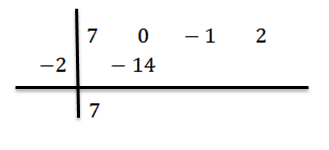
Lisäämme ja jatkamme, kuten aiemmin selitettiin, kunnes saavutamme viimeisen kauden:

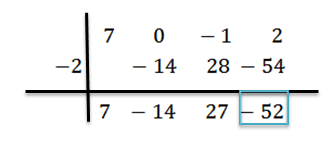
Tässä tapauksessa loput ovat r (x) = -52 ja saatu osuus on q (x) = 7x²-14x+27.

Esimerkki 3

Toinen tapa käyttää synteettistä jakoa on seuraava.

Jakoalgoritmille voimme kirjoittaa p (x) -polynomin seuraavasti:

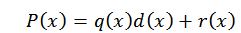
Tässä lausekkeessa q (x) ja r (x) ovat vastaavasti osamäärä ja loput. Nyt, jos d (x) = x-c, arvioitaessa C: ssä polynomista löydämme seuraavat:

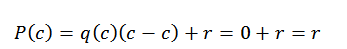
Siksi vain R (x): n löytäminen on edelleen, ja voimme tehdä tämän synteettisen jaon ansiosta.

Esimerkiksi meillä on polynomi p (x) = x⁷-9x⁶+19x⁵+12x⁴-3x³+19x²-37x-37 ja haluamme tietää, mikä sen arvo on arvioitaessa sitä x = 5. Tätä varten suoritamme jaon p (x) ja d (x) = x -5: n välillä synteettisellä jakautumismenetelmällä:

Voi palvella sinua: Aksiaalinen symmetria: Ominaisuudet, esimerkit ja harjoitukset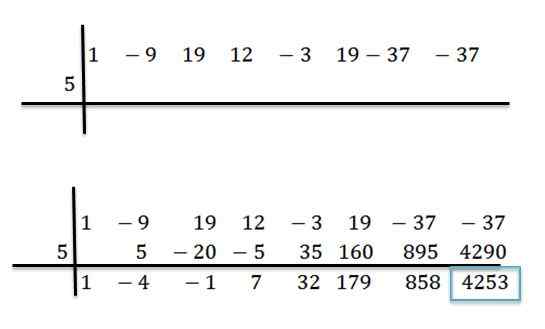

Kun toiminnot on tehty, tiedämme, että voimme kirjoittaa p (x) seuraavasti:

P (x) = (x⁶-4x⁵ -x⁴+ 7x³ +32x² +179x + 858)*(x-5) + 4253

Siksi sen arvioitaessa meidän on:

P (5) = (5-4 (5) -5 +7 (5) +32 (5) +179 (5) +858)*(5-5) +4253

P (5) = (5-4 (5) -5 +7 (5) +32 (5) +179 (5) +858)*(0) +4253

P (5) = 0 + 4253 = 4253

Kuten voimme nähdä, on mahdollista käyttää synteettistä jakautumista polynomin arvon löytämiseen arvioitaessa sitä C: ssä sen sijaan, että vain korvataan c x: llä. 

Jos yritämme arvioida P (5) perinteisellä tavalla, tarvitsemme joitain laskelmia, jotka yleensä muuttuvat tylsiksi.

Esimerkki 4

Polynomien jakautumisalgoritmi täyttyy myös polynomeille, joilla on kompleksikertoimia, ja seurauksena meillä on, että synteettinen jakautumismenetelmä toimii myös näille polynomeille. Seuraavaksi näemme esimerkin.

Käytämme synteettistä jakautumista menetelmää osoittaaksemme, että z = 1+ 2i on nolla polynomista p (x) = x³+ (1+i) x² -(1+2i) x+(15+5i). Toisin sanoen jaon P (x) jäännös d (x) = x - z: n välillä on yhtä suuri kuin nolla.

Jatkamme kuten aiemmin: Ensimmäisessä rivissä kirjoitamme P (x) -kertoimet, sitten toisessa kirjoitamme z: n ja piirtämme jakoviivat.

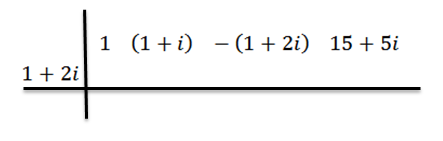
Teemme divisioonan kuten aiemmin, se on:

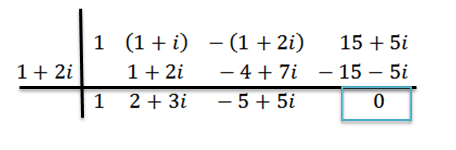
Voimme nähdä, että jäännös on nolla; Siksi päättelemme, että z = 1+ 2i on nolla p (x).

Viitteet

1. Kalju, aurelio. Algebra. Patria -toimitusryhmä.
2. Demana, Waits, Foley & Kennedy. Precáculo: graafinen, numeerinen, algebrallinen. Pearson -koulutus.