Arrhenius -yhtälö
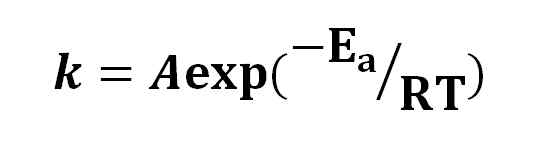
- 3751
- 1075
- Kelly Kilback
Mikä on Arrhenius -yhtälö?
Se Arrhenius -yhtälö Se on lähestymistapa, joka yhdistää kemiallisen reaktion nopeusvakion lämpötilasta riippuen. Sen perusti vuonna 1899 ruotsalainen kemisti Svante Arrhenius (1859-1927). Edustaa yhtä perustavanlaatuisimmista panoksista kemiallisen kinetiikan kehittämisessä.
Tämä yhtälö velkaa teoreettiset perustansa lukuisille tutkijoille, mukaan lukien Wihelmy (1850), Berthelot (1862) ja J. J -. Hood (1885). Mutta suurin vaikutus johtuu Arrhenius -yhtälön luomisesta Van't Hoofin (1884) tekemälle työlle, joka perusti riippuvuuden kemiallisten reaktioiden tasapainovakioista lämpötilan kanssa.
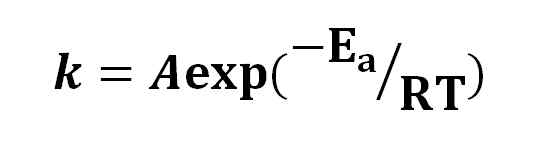 Arrhenius -yhtälö. Lähde: Gabriel Bolívar.
Arrhenius -yhtälö. Lähde: Gabriel Bolívar. Arrhenius -yhtälön perusteella ajatus siitä, että 10 ºC: n kasvu on aiheuttanut reaktionopeuden päällekkäisyyden, on levitetty. Muut tulkinnat, joista tulee, on, että molekyylit tarvitsevat jonkin verran aktivointienergiaa reagoidakseen toisiinsa.
Samoin huomautetaan, että Arrhenius -yhtälö on toinen eksponentiaalisen hajoamisen muoto, jossa nopeusvakion arvo eksponentista -e-lla/RT, missä E-lla on aktivointienergia.
Yhtälö ja selitys
Arrhenius -yhtälöllä on seuraavat kaksi lauseketta:
K = AE-EA/RT
Kemiassa käytetyn yhtälön muoto ja liittyy reagenssimoleihin.
K = AE-EA/KBT
Fysiikassa käytetyn yhtälön muoto ja liittyy enemmän molekyyleihin kuin mooliin.
Molemmat johdetaan vann kato -yhtälöstä tasapainovakion k variaatiolle lämpötilasta riippuen. Perusyhtälö on:
d (ln k)/dt = e-lla/RT2
Se voi palvella sinua: Dibenzalacetona: Ominaisuudet, reaktiomekanismi, käyttö, riskitJoka on integroitu olettaen-lla on riippumaton lämpötilasta. Joten meillä on:
ln k = - e-lla/Rt + ln a
Missä ln a on integraatiovakio. Kun eksponentiaalinen funktio sovelletaan yhtälön molemmille puolille, saadaan jo käyttöön otetun Arrhenius -yhtälön.
Komponentit
k -k -
Se on kemiallisen reaktion nopeusvakio. Sen arvoa voidaan saada Arrhenius -yhtälön käytön lisäksi nopeuslain soveltamalla. Edustaa reaktiolla tuotettujen hiukkasten välisten törmäysten lukumäärää.
-Lla
Se on ns. Exponentiaalinen tekijä, joka edustaa reagenssimolekyylien välisten törmäysten tiheyttä, jolla on asianmukainen geometrinen suuntaus. Jos lämpötilan vaihtelu on vähän suurta, sitä pidetään yleensä vakiona. Tällä tekijällä on oma kaava:
A = z ρ
Missä Z tunnetaan taajuus- tai törmäyskertoimena ja ρ geometrinen tai steerinen tekijä, joka osoittaa molekyylien suhteellisen suuntauksen törmäyspisteessä. Vakiona A on samat yksiköt kuin nopeusvakio. Jos aktivointienergiaa ei ole, A: n suuruus on yhtä suuri kuin k.
JA-lla
Se on aktivointienergia, joka edustaa kynnysenergiaa ennen siirtymätilanteen saavuttamista.
Aktivointienergialla on KJ/mol -yksikkö. Mutta laskelmissa J/mol käytetään yksikönä. Vähiten (-) merkki, joka edeltää E: tä-lla, Sen tarkoituksena on osoittaa, että sen kasvu tuottaa reaktionopeuden vähentyneen, samoin kuin sen lasku tuottaa reaktionopeuden lisääntymisen.
Voi palvella sinua: kaasukromatografiaRt
Edustaa keskimääräistä kineettistä energiaa. Samaan aikaan R on kaasujen yleinen vakio, joka on yksi sen eniten käytetyistä arvoista 8.31 J · K-1· Mol-1. Ja t on Kelvinissä ilmaistu absoluuttinen lämpötila (k).
ja
Se on luonnollisten tai Neperian logaritmien perusta, jonka arvo on 2.71828.
ja-EA/RT
Se on reagoivien molekyylien osuus yhtä suuresta tai ylimääräisestä energiasta suhteessa aktivointienergiaan.
Sovellukset
Suurin osa Arrhenius -yhtälön sovelluksista tulee käytöstä nopeusvakion määrittämisessä; ja laajennuksella, reaktion nopeus ja sen aktivointienergia.
Esimerkiksi kemiallinen malli on kehitetty Arrhenius -yhtälön perusteella, joka voi ennustaa materiaalien ominaisuudet niiden lämpötilan muutoksena, jota käytetään geologian, rakentamisen, materiaalien tekniikan ja elintarviketieteiden aloilla.
Sitä on sovellettu, vaikka tietyllä kritiikillä, Arrhenius -yhtälöä solid -tilan reaktioiden kinetiikassa. Sitä on käytetty myös kasvien vastausten karakterisoimiseksi vesistressille.
Arenhius -yhtälö toimi perustana matemaattisen mallin luomiselle, joka kvantifioi lämpötilan vaikutuksen nikkelimetallisten hydridisolujen tai paristojen käyttöikään.
Samoin perustuen Arrhenius -yhtälön, sikajätteiden hajoamisnopeus ja keittoöljy määritettiin, erilaisten kosteuspitoisuuksien mukaan.
Ratkaisut
Harjoitus 1
Mikä on reaktion aktivointienergia, jos havaitaan, että sen nopeusvakio kolminkertaiset lämpötilan noustessa 600 K - 610 K?
Voi palvella sinua: fenoksietikkahappo: synteesi, menettely, käyttö, riskitAlkaen Arrhenius -yhtälöstä:
k = a · e-EA/RT
Tyhjennämme tekijän A:
A = k1 / (e-EA/RT1-A
Mutta koska meillä on kaksi lämpötilaa, t1 ja T2, Nopeusvakioita on kaksi: k1 ja k2. Tekijä A ei muutu, joten voimme sovittaa sen toiseen lämpötilaan:
k -k -1 / (e-EA/RT1) = k2 / (e-EA/RT2-A
Ja puhdistaminen E-lla meillä tulee olemaan:
JA-lla = R (ln k2/k1) / (1 / t1 - 1/t2-A
Kuten mitä2 on kolme kertaa suurempi kuin k1,
k -k -2 / k1 = 3
ln (3) = 1.099
Ja toisaalta:
1 / t1 = 1/600 K = 1.66 x 10-3 K -k --1
1 / t2 = 1/610 K = 1.64 x 10-3 K -k --1
Silloin korvaaminen:
JA-lla = (8.31 J · K-1· Mol-1) (1.099) / (1.66 x 10-3 K -k --1 - 1.64 x 10-3 K -k --1-A
= 456.5 kJ · mol-1
Harjoitus 2
Kaasuhereaktiossa aktivointienergia on yhtä suuri kuin 103 kJ/mol, ja nopeusvakio on 0.085 min-1. Laske nopeusvakio 323 K: ssa.
Edellisestä lausekkeesta selvitämme ln k2/k1-
ln k2/k1 = (E-lla/R) (1 /t1 - 1/t2-A
Yhtälön oikean osan kehittäminen:
ln k2/k1 = (103.000 j · mol-1 / 8.31 J · K-1· Mol-1) (1/273 K - 1/323 K)
ln k2/k1 = 6.99
Antilogaritmien ottaminen:
k -k -2/k1 = 1.086
k -k -2 = (k1) (1.086)
= (0.085 min-1) (1.086)
= 0.092 min-1
Viitteet
- Whitten, Davis, Peck & Stanley. (2008). Kemia. (8. ed.-A. Cengage -oppiminen.
- Walter J. Moore. (1963). Fysikaalinen kemia. Kemiallisessa kinetiikassa. Neljäs painos, Longmans.
- Iranin. Levine. (2009). Fysikaalis -periaatteet. Kuudes painos. MC Graw Hill.
- Wikipedia. (2020). Arrhenius -yhtälö. Haettu: vuonna.Wikipedia.org
- Guenevieve del Mundo et ai. (10. syyskuuta 2020). Arrhenius -yhtälö. Palautettu: Chem.Librettexts.org
- Clark Jim. (2013). Nopeusvakiot ja Arrhenius -yhtälö. Talteenotettu: Chemguide.yhteistyö.Yhdistynyt kuningaskunta
- Enyclopaedia Britannica -toimittajat. (2020). Arrhenius -yhtälö. Toipunut: Britannica.com
- Helmestine, Anne Marie, PH.D -d. (28. elokuuta 2020). Arrhenius -yhtälön kaava ja esimerkki. Toipunut: Admingco.com

