Yleinen yhtälö linjasta, jonka kaltevuus on yhtä suuri kuin 2/3

Linjan L yleinen yhtälö on seuraava: AX+By+C = 0, missä a, b ja c ovat vakioita, x on riippumaton muuttuja E ja riippuvainen muuttuja.

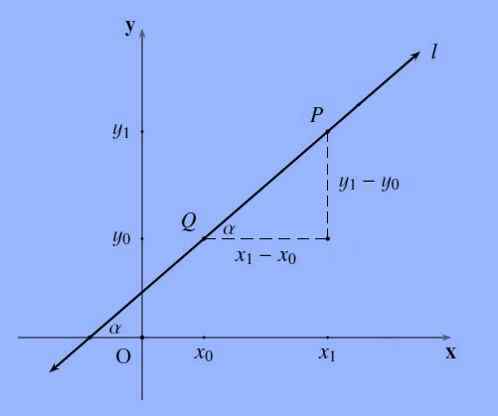
Linjan kaltevuus, joka on merkitty yleisellä tavalla kirjaimella M, joka kulkee pisteiden p = (x1, y1) ja q = (x0, y0) läpi, on seuraava jakaminen m: = (y1-y0)/(x1 -X0).

Suoran viivan kaltevuus edustaa kaltevuutta; Sanotaan muodollisemmin, viivan kaltevuus on kulman tangentti, jonka tämä muoto X -akselilla.

On huomattava, että pisteiden nimeämisjärjestys on välinpitämätön, koska (y0-y1)/(x0-x1) =-(y1-y0)/(-(x1-x0)) = (y1-y0) /(X1-x0).

Vireillä oleva linja

Jos tiedetään kaksi pistettä, jonka kautta linja kulkee, sen kaltevuus on helppo laskea. Mutta mitä tapahtuu, jos näitä kohtia ei tunneta?

Kun otetaan huomioon kirves+c = 0 -rivi, sen on oltava.

Mikä on linjan yleinen yhtälö, jonka kaltevuus on 2/3?

Koska viivan kaltevuus on 2/3, tasa -arvo muodostetaan -a/b = 2/3, mikä näkee, että a = -2 ja b = 3. Niin, että viivan yleinen yhtälö, jonka kaltevuus on yhtä suuri kuin 2/3, on -2x+3y+c = 0.

On selvennettävä, että jos sinut valitaan a = 2 ja b = -3, sama yhtälö saadaan. Itse asiassa 2x -3y+c = 0, joka on yhtä suuri kuin edellinen kerrottuna -1: llä. C -merkinnällä ei ole merkitystä, koska se on yleinen vakio.

Toinen havainto, joka voidaan tehdä. Tässä tapauksessa yleinen yhtälö on -4x+6y+c = 0.

Onko olemassa muita tapoja löytää viivan yleinen yhtälö?

Vastaus on kyllä. Jos viivan kaltevuus tunnetaan, on olemassa kaksi muotoa, jotka ovat edellisen lisäksi, yleisen yhtälön löytämiseksi.

Tätä varten käytetään pistettä odotettavaa yhtälöä ja leikkausyhtälöä.

-Pistettä odotettavaa yhtälöä: Jos m on viivan kaltevuus ja p = (x0, y0) piste, jossa se kulkee, niin yhtälö y-y0 = m (x-x0) kutsutaan pisteviivaiseksi yhtälöksi.

-Leikkauslähetysyhtälö: Jos m on viivan kaltevuus ja (0, b) on viivan leikkaus Y-akselin kanssa, niin yhtälöä y = mx+b kutsutaan leikkausviivan yhtälön kanssa.

Ensimmäistä tapausta käyttämällä saadaan, että viivan pisteessä oleva yhtälö, jonka kaltevuus on 2/3, annetaan lausekkeella y-y0 = (2/3) (x-x0).

Yleisen yhtälön saavuttamiseksi kaikki termit kerrotaan 3: lla molemmilla puolilla ja ryhmitelty toisiinsa, mikä saa siten -2x+3y+(2 × 0-3Y0) = 0 on viivan yleinen yhtälö, jossa c = 2 × 0-3Y0.

Jos toista tapausta käytetään, saadaan, että viivan leikkausyhtälö, jonka kaltevuus on 2/3, on y = (2/3) x+b.

Jälleen kerrotaan 3 molemmin puolin ja ryhmittelemällä kaikki muuttujat, se saadaan -2x+3y -3b = 0. Jälkimmäinen on linjan yleinen yhtälö, jossa c = -3b.

Itse asiassa tarkkaan molemmissa tapauksissa voidaan nähdä, että toinen tapaus on yksinkertaisesti ensimmäinen tapaus (kun x0 = 0).