Murto -yhtälöt

Murto -yhtälöt sisältävät numeeriset ja/tai algebralliset fraktiot, ja tuntematon voi olla sekä numeraattorissa että nimittäjässä tai molemmat

Mitkä ovat murto -yhtälöt?

Se murto -yhtälöt ovatko ne, jotka sisältävät fraktioita yhdessä tai useammassa termissaan. Tällaiset fraktiot voivat olla numeerisia tai algebrallisia, missä tuntematon löytyy numeraattorista ja/tai minkä tahansa termin nimittäjästä.

Sitten joitain esimerkkejä murto -yhtälöistä yhdellä tuntemattomalla:

Ensimmäinen esimerkki on lineaarinen yhtälö, jossa on murtokertoimet; Toisessa esimerkissä tuntematon on kunkin termin nimittäjä, ja viimeisessä tuntematon on sekä numeroija että nimittäjässä.

Niiden ratkaisemiseksi on tarpeen suorittaa joitain algebrallisia muunnoksia ja saada siten vastaava yhtälö, jossa tuntematon ei näy nimittäjässä. Kun tämä menettely on suoritettu, ratkaisu löytyy sopivilla tekniikoilla.

Ratkaisu koostuu tasa -arvon tyydyttävistä “x” -arvoista. Se voi olla ainutlaatuinen arvo tai useita, mutta joka tapauksessa on erittäin tärkeää pitää mielessä, että kaikki vastaavan yhtälön ratkaisut eivät ole alkuperäisen yhtälön hyväksyttäviä.

Itse asiassa, jos se on yhtälö, jonka tuntematon on nimittäjässä, ”x” -arvot, jotka mitäöitävät sitä, on vältettävä, vaikka ne kuuluisivat vastaavien yhtälöratkaisujen joukkoon,. Tämä johtuu siitä, että jakoa 0 välillä ei ole määritelty.

Jos vastaavalla yhtälöllä on ainutlaatuinen ratkaisu, ja osoittautuu, että minkä tahansa alkuperäisen yhtälön ehtojen nimittäjä peruutetaan, niin siinä ei ole ratkaisua.

Kuinka ratkaista murto -yhtälö

Ei -vakavien yhtälöiden ratkaisemiseksi suoritetut toiminnot ovat päteviä, edellyttäen, että tasa -arvo ylläpidetään. Tällä tavalla voit lisätä tai vähentää saman määrän tasa -arvon molemmille puolille murto -yhtälöllä, kertoa kaikki termit samalla määrällä tai jakaa jokainen termi samalla määrällä (erilainen kuin 0).

Voi palvella sinua: Bolzano -lause

Mutta koska murto -yhtälö on välttämätöntä muuttua toiseen vastaajiksi ilman nimittäjiä, seuraavia yleisiä indikaatioita seuraa myös:

1. Löydä nimittäjien vähimmäismäärä (M.c.m).
2. Kerro jokainen termi M: llä.c.m., Nimittäjien poistamiseksi.
3. Ratkaise saatu vastaava yhtälö.
4. Varmista, että löydetyt ratkaisut tyydyttävät alkuperäisen tasa -arvon.

Tyypit vastaavat yhtälöt

Ehdotetun menettelyn mukaiset vastaavat yhtälöt voivat olla:

• Lineaarinen tai ensimmäinen aste
• Kvadraattinen
• Korkeamman asteen

Ratkaistu esimerkki

Esimerkki 1

Ratkaise seuraava yhtälö:

On huomattava, että yhtälö on ensimmäinen aste "X": ssä, koska "x" on korkea 1: ssä. Yhtälön kertoimet ovat fraktioita ja tapa eliminoida ne, työskennellä kokonaislukuilla, se kertoo kaikki termit nimittäjien vähimmäismäärällä (M.c.m.-A.

m.c.m. (2,3,6) = 6

Niin:

3x - 2x = 1

x = 1

Lukija voi tarkistaa tämän ratkaisun pätevyyden korvaamalla x = 1 alkuperäisessä yhtälössä ja varmistamalla, että tasa -arvo saadaan.

Esimerkki 2

Määritä X -arvot, jotka tyydyttävät:

Toisin kuin edellisessä esimerkissä, tässä tapauksessa tuntematon löytyy nimittäjästä. Huomaa, että nimittäjät on kumottu arvoille x = 2 ja x = −1, yksityiskohta, joka on kätevä ottaa huomioon, koska jos vastaava yhtälö myöntää nämä ratkaisut, meidän on hylättävä ne, koska niitä ei voida hyväksyä alkuperäisessä yhtälössä.

Nyt meidän on muutettava yhtälö toiseksi ilman nimittäjiä, ensimmäinen askel on tehdä termien summa tasa -arvon vasemmalle:

Koska nimittäjät ovat samat, niin että tasa -arvo toteutuu, on välttämätöntä, että myös numeroijat ovat:

Voi palvella sinua: Suhteellisuusvakio: Mikä on, laskenta, harjoitukset

4 (x+1) - 3 (x -2) = 8

Se riittää ratkaisemaan tämän yhtälön, joka osoittautuu ensimmäisen luokan:

4x + 4 - 3x + 6 = 8

x = 8 - 6 - 4 = - 2

x = - 2

Koska tämä arvo on erilainen kuin kielletyt arvot, se hyväksytään alkuperäisen yhtälön ratkaisuna.

Esimerkki 3

Löydä ratkaisu:

Tässä yhtälössä arvo x = 4 peruuttaa nimittäjät, siksi se suljetaan muunnosyhtälön liuosjoukon ulkopuolelle, jos se ilmestyi.

Muunnettu yhtälö on helppo löytää, se riittää kertomaan kaikki termit tekijän (x-4) avulla:

Pysyminen:

2x - 4 = 4

2x = 8

x = 4

Esimerkki 4

Ratkaise yhtälö:

Tässä tapauksessa nimittäjillä on neliömäiset termit, joten on kätevää ottaa ne ensin huomioon:

• x² + 8x + 7 = (x + 7) (x + 1)
• x² - 49 = (x + 7) (x - 7)
• x² - 6x - 7 = (x - 7) (x + 1)

Yhtälö on tällainen:

X: n arvot, jotka peruuttavat minkä tahansa nimittäjän, ovat: x = −7, x = 7, x = −1. Siksi, vaikka nämä arvot ovat osa modifioidun yhtälön ratkaisujoukkoa, ne eivät voi olla alkuperäisen yhtälön ratkaisu.

Nyt tulee yhtälön muuntamisprosessi. Ensimmäinen askel on löytää nimittäjien vähimmäisosaosa:

m.c.m. = (x + 7) (x - 7) (x + 1)

Kertomalla tasa -arvon molemmilla puolilla m.c.m. on jäljellä:

Tuloksena:

(x --7) (x - 2) = (x + 1) (2x - 5) - (x + 7) (x - 2)

Jakavan omaisuuden kautta tuotteita kehitetään:

x² - 9x +14 = 2x² - 3x - 5 - (x² + 5x - 14)

Vähentämällä samanlaisia ​​termejä oikealla puolella:

x² - 9x + 14 = x² - 8x + 9

Neliölliset ehdot peruutetaan täyttämällä sama merkki tasa -arvon eri puolilla:

Voi palvella sinua: Kuutiot: Kaavat, yhtälöt, esimerkit, harjoitukset

- 9x + 14 = - 8x + 9

-x = -5 ⇒ x = 5

Tämä tulos hyväksytään ratkaisuna, koska se ei ole mikään kielletty arvo.

Fraktioyhtälöiden käyttö käyttää

Firctionin nimittäjä ylittää neljä yksikköä osoittajalle. Jos osoitin vähennetään osoitimesta ja myös nimittäjästä, tuloksena oleva murto on 3/5. Määritä alkuperäinen osuus.

Ratkaisu

Olkoon x osoittajan arvo.

Koska murto -osan nimittäjä ylittää neljä yksikköä osoittajalle, alkuperäinen osa on:

Nyt sinun on vähennettävä 5 yksikköä, sekä numeroijalle että nimittäjälle:

Koska edellisen menettelyn suorittamisesta johtuva osuus on yhtä suuri kuin 3/5, ne tasoitetaan:

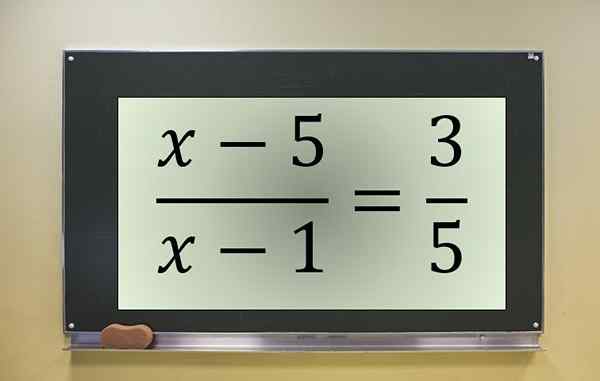Murto -yhtälöesimerkki. Lähde: f. Zapata.

Tämä on murto -yhtälö tuntemattoman kanssa numeroija ja nimittäjä, joka peruutetaan kohdassa x = 1. Siksi tämä arvo on suljettava pois, jos se olisi muunnetun yhtälön ratkaisujen joukossa.

Sitten se moninkertaistaa molemmat osapuolet vähimmäisvaatimuksella, joka on 5 (x - 1):

Tuloksena seuraava vastaava yhtälö:

5 (x - 5) = 3 (x - 1)

Jakavan omaisuuden soveltaminen:

5x -25 = 3x - 3 ⇒ 2x = 22

x = 11

Alkuperäinen osuus korvaa x = 11 lausekkeessa:

Tuloksena osittainen 11/15. Tämä on vastaus nostettuun ongelmaan.

Viitteet

1. Murto -yhtälöt. Toipunut: MathePower.com
2. Matematiikkaportaali. Murto -yhtälöt. Ongelmanratkaisu. Toipunut: Silviodarte.com.
3. Stewart, J. (2007). Precculment: Laskentamatematiikka. Viides. Painos. Cengage -oppiminen.
4. Sullivan, M. (1997). Ennakkoluulo. Neljäs. Painos. Pearson -koulutus.
5. Zill, D. (2008). Ennakkoluulo laskenta etenee. Neljäs. Painos. McGraw Hill.