Matematiikka

Ellipsi

Ellipsi
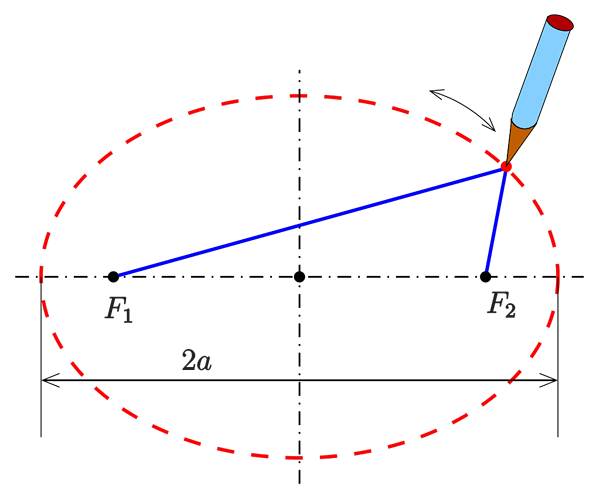
Kuvio 1. Puutarhurimenetelmä ellipsin piirtämiseksi. Ellipsin pisteen P (punaisella) ja valokeilojen (mustana) pisteen P: n välisten etäisyyksien summa pysyy vakiona. Lähde: AG2gaeh, CC BY-SA 4.0, Wikimedia Commons.

Mikä on ellipsi?

Ellipsi on joukko koordinaattipisteitä (x, y), joille etäisyyksien summa kahteen kiinteään pisteeseen, nimeltään Keskittyä, se on vakio. Kohdevalot puolestaan ​​erotetaan toisistaan ​​etäisyys, joka on yhtä suuri kuin 2C.

Ellipsit löytyvät luonnosta. Esimerkiksi, se on maan liikkeessä auringon ympärillä, koska saksalainen tähtitiede osoittaa.

Lisäksi elliptinen muoto löytyy arkkitehtonisten rakenteiden suunnittelusta, se on osa lääketieteellistä hoitoa munuaislaskelmien tuhoamiseksi ja sen tarkoituksena on muokata erilaisia ​​esineitä, kuten säiliöitä ja muita astioita.

Yläkuviossa ellipsi on esitetty kahdella valokeilalla, jotka sijaitsevat yhtä kaukana kuvion keskustasta ja pisimmästä akselista. Edellytys, että pisteen P on täytettävä kuulumiseksi ellipsiin, on, että etäisyyksien summa jokaiseen tarkennukseen on kiinnitetty:

d -d1 + d -d2 = vakio.

Siksi, kun puutarhuri haluaa. Ota sitten hyvä kokoinen köysi, sido sen päät panoksiin ja köyden sauvan tukeminen liukuu sen päälle merkitsemään pehmeän maan elliptistä ura. Tämä on puutarhurimenetelmä Piirtää ellipsejä.

Elipse -elementit

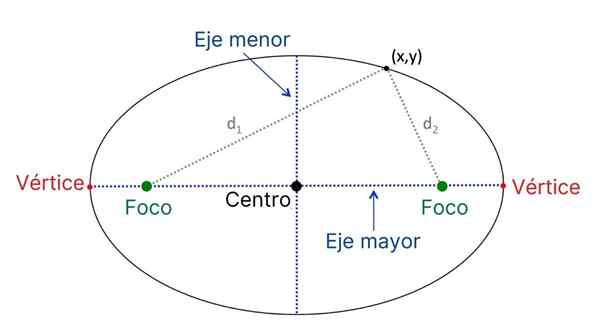Ellipsin pääelementit

Nämä ovat ellipsin pääelementit:

  1. Keskittyä, Kiinteät pisteet, jotka sijaitsevat ellipsin pisin akseli.
  2. Kärjet, Ne ovat sen ellipsin kaksi pistettä, joiden läpi linja kulkee, joka liittyy valokeilaan.
  3. Pääakseli, Se on köyttä, joka liittyy kärkipisteisiin ja sisältää myös valokeilut.
  4. Keskusta, Pääakselin keskimmäinen kohta, joka vastaa koordinaattipistettä (H, K). Jokainen tarkennus on yhtä kaukana keskustasta ja etäisyydestä c samasta.
  5. Akseli, Köysi kulkee keskustan läpi ja on kohtisuorassa pääakseliin nähden.
  6. Vektoriradiot, Segmentit, jotka yhdistävät kukin keskittyvät ellipsin p: llä.
  7. Polttoakseli, suoraan, joihin valokeilut ovat.
  8. Polttomatka, Se on etäisyys valonheittimien välillä, merkitty 2c: ksi.
  9. Toissijainen akseli, Akseli, joka on kohtisuorassa pääakseliin, joka on samanaikaisesti segmentin megmentin mediatrix, joka sitoutuu valokeilaan.
  10. Symmetriakeskus, Piste on samat kuin ellipsin keskusta, jossa saman symmetrian akselit ristissä on ristissä.
  11. Symmetria -akselit, linjat, jotka sisältävät ellipsin suurimmat ja pienemmät akselit.
Voi palvella sinua: verotus

Tyypit ellipse

Ellipsejä on kahta tyyppiä:

  • Ne, joilla on pääakseli vaaka.
  • Ne, joilla on suurin pystysuora akseli.

Sitten ne kuvataan matemaattisesti:

Ellipse suurten vaakasuoran akselin kanssa

Olkoon osoitus koordinaattien (h, k) ellipsin keskipiste, pääakselin pituus on 2a ja pienemmän akselin pituus, joka on yhtä suuri kuin 2B, a> b.

Tämän ellipsin yhtälö on:

Ellipse pääasemakselilla

Samoilla ellipsin parametreilla, joissa on vaakasuora akseli, ellipsi pääasiansa kanssa kirjoitetaan seuraavasti:

Molemmissa tapauksissa etäisyys keskittymisestä keskustaan c Se liittyy sedimenteihin pääaineisiin ja alaikäisiin:

c2 = a2 - b2

Esimerkkejä ellipseistä

Vaakasuuntainen ellipsi

Seuraava kuva näyttää ellipsin, jonka pääakseli on vaakasuora. Keskusta on pisteessä (0,0) ja vastaavasti (-3,0) ja (3.0) kohdevalot. Piste P (0, -4) korostettu kuuluu ellipsiin.

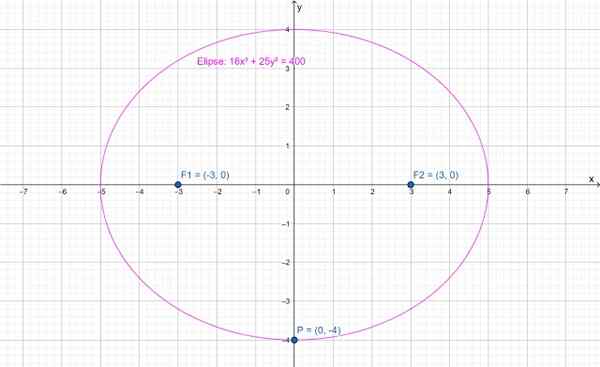Kuva 2.- Ellipsi, jonka pääakseli on vaakasuora. Lähde: f. Zapata Geogebran kautta.

Tämän ellipsin yhtälö on:

16x2 + 25 ja2 = 400

Tätä yhtälöä ei ole vaikea ilmaista kanonisessa muodossa, se riittää jakamaan kaikki termit 400: n välillä ja yksinkertaistamaan kätevästi (katso harjoitus ratkaistu myöhemmin).

Pystysuuntainen ellipsi

Seuraava on pystysuora ellipsi, jonka pääakseli on samaan aikaan akselin ja. Se on keskittynyt pisteeseen (0,0) ja sen yhtälö on:

36x2 + 9y2 = 324

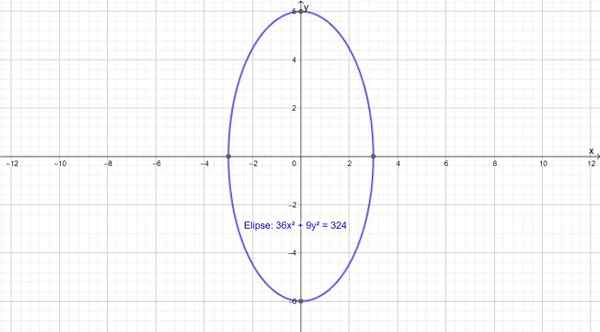Kuva 3.- Ellipsi suuren pystysuoran akselin kanssa. Lähde: f. Zapata Geogebran kautta.

Heijastusominaisuus

Se koostuu seuraavista: Jos heijastin tai äänilähde sijoitetaan johonkin ellipsin valonheittimeen, emittoidut aallot heijastuvat kohti toista keskittymistä. Se on hyvä tapa ohjata aaltoja, joissa energiasi tarvitaan.

Voi palvella sinua: Endecagon

Siksi elliptisissä salissa, kun henkilö puhuu yhdessä ollessa yhdessä valokeilassa, toisessa painopisteessä oleva kuuntelija kuuntelee selvästi.

Ja lääketieteessä tätä heijastusominaisuutta käytetään munuaiskivien tuhoamiseen asettamalla potilas johonkin vettä täynnä olevan elliptisen kylpyammeen valokeilaan, kun taas ultraääni -aaltogeneraattori on sijoitettu toiseen tarkennukseen. Aallot heijastuvat laskelmissa ja pirstoutuvat ne pienemmissä hiukkasissa, jotka sitten karkotetaan virtsan läpi.

Ska -radio

Tämä radioteleskooppi on tyypiltään suurin, ja sen odotetaan alkavan toimimaan vuonna 2021. Sen pinta on 1 km neliö ja siksi sitä kutsutaan SKA: sta (englanniksi ne ovat lyhenne Neliökilometrin taulukko-A.

Hyödyntäen ellipsien heijastusominaisuutta, rakenne koostuu 3000 antennista, jonka elliptinen muoto on noin 15 m leveä, jaettu Australian ja Etelä -Afrikan kesken. Tämän instrumentin kanssa, 50 kertaa herkempi kuin tällä hetkellä käytössä olevat, odotetaan katsovan maailmankaikkeutta, kun se oli vielä paljon nuorempi: noin miljardi vuotta tuskin.

Kuva 4.- SKA Radio Ska -sarjan taiteellinen tulkinta. Lähde: Wikimedia Commons.

Liikuntaa

Löydä kuvioissa 2 ja 3 esitettyjen ellipsien kanoniset yhtälöt ja määritä kussakin tapauksessa aistien pituudet suuremmat ja pienemmät, samoin kuin polttomatkat.

Ratkaisu

Vaaka ellipsissä, jonka yhtälö on 16x2 + 25 ja2 = 400, kaikki termit 400: n välillä on jaettu, tuloksena:

Voi palvella sinua: Kohdosta johdettu: Laskenta, esittely, harjoitukset

 Jota yksinkertaistetaan:

Puoli -akseli “A” mittaa 5 ja pienin “B” mittaa 4, jota myös varoitetaan tarkkailemalla kuvaa huolellisesti. Mitä tulee keskietäisyyteen, sinun on:

c2 = a2 - b2

c2 = 25 - 16 = 9 ⇒ C = √9 = 3

Siksi c = 3 on keskuksen ja yhden valokeilan välinen etäisyys. Molemmat polttoaineet ovat etäisyys 2c = 6.

Pystysuoraan ellipsi 36x2 + 9y2 = 324 Sinulla on:

Yksinkertaistamalla:

c2 = 36 - 9 = 27

C = √27 ≅ 5.2

Siksi valokeilojen välinen etäisyys on 10.4 yksikköä.

Viitteet

  1. Hoffman, J. Matematiikan aiheiden valinta. Osa 3.
  2. Stewart, J. 2006. Precculment: Laskentamatematiikka. Viides. Painos. Cengage -oppiminen.
  3. Maailmankaikkeuden kaavat. Ellipsi. Toipunut: UniversOformulat.com.
  4. Wikipedia. Neliökilometrin taulukko. Palautettu: on.Wikipedia.org.
  5. Zill, D. 1984. Algebra ja trigonometria. McGraw Hill.