Jännitystesti miten se tehdään, ominaisuudet, esimerkit

Eräs jännityskoe Se on kokeellinen testi, joka suoritetaan materiaalinäytteelle sen määrittämiseksi. Sen ansiosta voit tuntea monia materiaalin mekaanisia ominaisuuksia ja selvittää, onko se sopiva tietylle suunnittelulle.

Näyte on yleensä sylinteri, nimeltään koeputki. Tähän kohdistuu jännitys, joka koostuu kahden vastakkaisen voiman soveltamisesta päihin, jotka venyttävät palkkia ja muodostuvat sen. Essee jatkaa kasvavia ponnisteluja, kunnes näyte lopulta rikkoutuu.

Kuvio 1. Jännitekone. Lähde: Wikimedia Commons.

Huomaa niiden voimien suuruudesta ja muodonmuutoksista, joita ne tuottavat näytteessä, pienistä voimista, jotka eivät aiheuta pysyviä muodonmuutoksia, kappaleen murtumisen aiheuttamaan jännitykseen.

Siellä päättyy tiedonkeruun ja ponnistelujen kaavioon on kehitetty, mikä auttaa analysoimaan materiaalien, kuten metallien, keramiikan, sementin, puun ja polymeerien, käyttäytymistä.

[TOC]

Mitä käytetään jännityskokeessa?

Kokeilu tekee erityiskoneet, kuten kuvassa 1 esitetyt, jotka tarjoavat tarvittavat pyrkimykset lataamiseen ja lataavat materiaalin sitten muodonmuutoksen arvioimiseksi.

Näytteen osalta se on putki, jolla on vakio poikkileikkaus, lieriömäisessä, suorakaiteen muotoisessa tai neliömessä, jonka mitat on standardisoitu. Äärimmäiset ovat leveämpiä näytteen alistamisen helpottamiseksi, kuten kuvassa 2 on jäljellä.

Alkuperäinen pituus l_jompikumpi Näytteen putken kalibroitu alue mitataan ja merkitään. Sitten leuat pitävät sitä testikoneessa ja tämä alkaa.

Kuva 2. Vasemmalla puolella teräsputki ja oikea sama näyte jo murtunut. Jännitystesti on tuhoisa testi. Lähde: Wikimedia Commons.

Saadut ominaisuudet ja tiedot

Materiaaleilla on erilaisia ​​käyttäytymisiä jännityksen edessä, joka on esitetty seuraavassa kaaviossa, jota varten terästä käytettiin. Pystysuuntaisella akselilla sovelletut ponnistelut merkitään kreikkalaisella kirjaimella σ ja vaakasuoran akselin yhtenäisen muodonmuutoksen, nimeltään ε.

Se voi palvella sinua: Rutherford Atomic -malli: Historia, kokeet, postulaatit

Yhtenäisellä muodonmuutoksella ei ole ulottuvuuksia, koska testin pituuden Δ = l välillä on osoitus_F - Lens_jompikumpi ja alkuperäinen pituus. Niin:

ε = ΔL / L_jompikumpi

Ponnistelujen suuruus σ on puolestaan ​​voima/ristikkäinen syy.

Kaaviossa erotetaan kaksi tärkeää aluetta: elastinen vyöhyke ja muovivyöhyke.

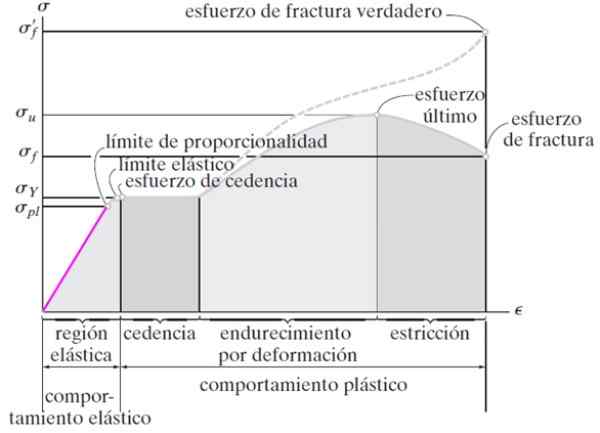Kuva 3. Teräspyrkimyskäyrä. Lähde: Materiaalimekaniikka. Hibbeler, R.

Joustava alue

Kun jännityspyrkimys σ on pieni, muodonmuutos on verrannollinen, niin kutsutaan Hooken laki:

σ = y ε

Kun ponnistus lakkaa, runko palaa alkuperäisiin mittoihinsa. Tämä on kuvion 3 värillinen elastinen alue, joka ulottuu nimeltään pisteeseen suhteellisuusraja. Toistaiseksi materiaali noudattaa Hooken lakia.

Suhteellisuusvakio ja on Nuori moduuli, Materiaalille ominainen ja joka voidaan määrittää jännitys- ja puristuskokeista.

Youngin moduulilla on paineyksiköt kansainvälisessä järjestelmässä [y] = n / m^2 = pa. Yhtenäinen muodonmuutos on, kuten jo sanottu, ulottumaton, siksi ponnistelu σ: lla on myös voiman mitat poikkileikkausosastoyksikköä kohti ja SI: ssä sen yksikkö on Pascal: [σ] = N/ M^2 = PA.

Suhteellisuusrajasta ja pyrkimyksen lisääminen etenee alueella, jolla muodonmuutos on palautuvaa, mutta ei noudata Hooken lakia. Päättyy kohtaan, josta runko on muodonmuutos, nimeltään joustava raja.

Muovivyöhyke   

Sitten materiaali tulee muovikäyttäytymisalueelle. Kun joustavan käyttäytymisen pinta -ala on ylitetty, teräs tulee Tuottopyrkimys tai hiipiä, jossa näyte on muodonmuutos, mutta ei rikko, vaikka ponnistus pysyy vakiona σ: ssa_JA.

Voi palvella sinua: Lämpölaajennus

Siirtovyöhykkeen voittaminen muodonmuutos kasvaa sovellettaessa, mutta ei enää lineaarisella tavalla.

Materiaalikokemukset muuttuvat molekyylitasolla ja kovettuminen muodonmuutoksella tapahtuu. Siksi näemme, että muodonmuutoksen saavuttamiseksi tarvitaan kasvavia ponnisteluja.

Tämän alueen raja on Viimeistä ponnisteluja. Materiaalia pidetään rikki tässä vaiheessa, vaikka näyte on edelleen kappaleessa. Sieltä tarvittava kuorma muodonmuutoksen tuottamiseksi vähenee ja näyte ohennetaan asteittain (tiukka) kunnes lopulta murtumat (kuva 2, oikea).

Tätä käyrää ja sen alueita kutsutaan tavanomaisiksi murtumispyriksi. Mutta hänen päällään on epäjatkuva käyrä, nimeltään Todellinen murtumapyrkimys, joka saadaan rekisteröimällä näytteen välitön tai todellinen pituus sen sijaan, että työskentelisit alkuperäisen pituuden kanssa yhtenäisen muodonmuutoksen löytämiseksi, kuten alussa selitetään.

Molemmat käyrät, tosi ja tavanomainen, osuvat samanaikaisesti pienten ponnistelujen alueella zidance -vyöhykkeelle. Joka tapauksessa materiaalin odotetaan toimivan elastisella alueella pysyvien muodonmuutosten välttämiseksi, jotka estävät valmistetun kappaleen asianmukaisen toiminnan.

Joten kokeesta saatujen tärkeimpien tietojen joukossa ovat ponnistus σ_JA joka määrittelee joustavan rajan.

Esimerkkejä jännitystesteistä

Materiaali, jota käytettiin mallina edellisessä kuvauksessa, on teräs, jonka käyttöä laajennetaan laajasti rakentamiseen ja teollisuuteen. Mutta on monia materiaaleja, kuten betonia, betonia, erilaisia ​​metalleja, seoksia ja puuta, joita käytetään myös laajasti.

Voi palvella sinua: Termodynaaminen järjestelmä: Ominaisuudet, tyypit, esimerkit

Jokaisella on ominaista ponnistelukäyrä, ja heidän vasteensa jännitteeseen tai pitoisuuteen ne luokitellaan kahteen luokkaan: herkkä tai palloke.

Hauraita ja palloke -materiaaleja

Seuraavassa kaaviossa σ vs. ε (Stressi rasitus) hauraita materiaaleja verrataan (Hauras) ja kanavat (kanavat), vaikka on tarpeen selventää, että samalla materiaalilla voi olla yksi tai toinen vaste sellaisista tekijöistä riippuen. Materiaalit ovat alhaisissa lämpötiloissa yleensä hauraita.

Merkittävä ero näiden kahden välillä on, että herkästä materiaalista puuttuu satoalue tai sillä on hyvin pieni. Heti kun joustava raja ylittää näytteen, on rikki. Toisaalta palloke -materiaalit absorboivat enemmän energiaa ennen murtumista, koska niillä on laaja muovivyöhyke.

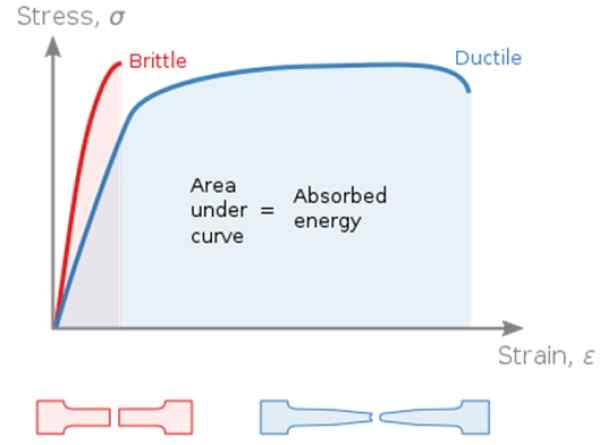Kuva 4. Ductive-materiaalien ja hauras materiaalien pyrkimyskäyrä. Lähde: Wikimedia Commons.

Jännitystesti on hyödyllinen materiaalin luokittelemiseksi, mikä on edullinen, kun muotoilukerroksen käytön levitys.

On myös huomattava, että vaikka jotkut materiaalit ovat hauraita jännityksessä, muut ponnistelut voivat vastustaa paremmin, kuten alla näemme.

Eri materiaalien vaste jännitestiin

-Harmaa valurauta: Hauras jännitys, vastustuskykyisempi puristuksessa.

-Pronssi:.

-Betoni: Hauras sekoitustyypistä riippuen, mutta erittäin kestävä puristuksessa. Kun se on jännitteellä, se vaatii teräspalkkien vahvistamista.

-Puu: Alkuperän mukaan hän on kohtalaisen ulottuva.

-Teräs: Herkkä, kun sinulla on korkea hiilipitoisuus.

-Metakrylaatti: Ductive, kun lämpötilaa nostetaan.

Viitteet

1. Olut, f. 2010. Materiaalimekaniikka. McGraw Hill. Viides. Painos.
2. Cavazos, j.Lens. Materiaalimekaniikka. Palautettu: YouTube.com.
3. Hibbeler, R. 2011. Materiaalimekaniikka. Kahdeksas painos. Pearson.
4. Collins, D. Lineaariset liikkeen kärjet. Materiaalien mekaaniset ominaisuudet: jännitys ja rasitus. Toipunut: LinearMotionips.com.
5. Valera Negrete, J. 2005. Yleiset fysiikan muistiinpanot. Yksinäinen.
6. Wikipedia. Vetokoe. Palautettu: on.Wikipedia.org.