Hess Selityslaki, hakemukset, esimerkit

Se Hess -laki Se on toinen osoitus energiansäästölaista, jonka avulla voidaan määrittää yksinkertaisten algebrallisten summien avulla kemiallisen reaktion entalpian avulla. Entalpian ymmärretään, kun lämpö vapautuu tai absorboitiin vakiopaineessa, joka liittyy mihin tahansa kemialliseen reaktioon tai kemialliseen ilmiöön.

Entalpit, ΔH, määritetään kokeellisesti kalorimetrialla. On kuitenkin reaktioita, joita on vaikea tutkia tällä tekniikalla. Kun näin tapahtuu, käytetään muita reaktioita, jotka heidän erityisillä entalpiaillaan on ja joilla on kiinnostuksen kohteet tai yhdisteet.

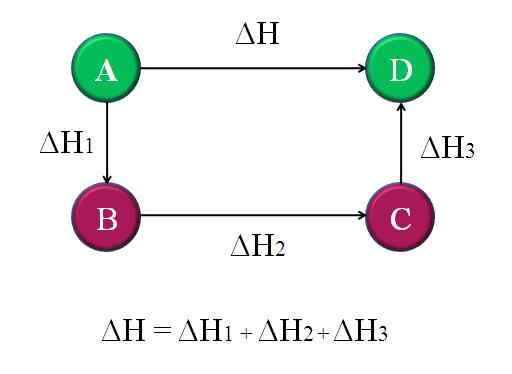
Yksinkertainen ja yleinen kaavio, jossa sovelletaan neljän kemiallisen reaktion hess -lakia. Lähde: Gabriel Bolívar.

Tällä tavalla voidaan laskea reaktion ”tuntematon” ΔH. Esimerkiksi ylin kaavio auttaa ymmärtämään tätä ajatusta. Reaktioita on neljä: A-D, A-B, B-C ja C-D. A-D-reaktio on se, jolla on suurin ΔH, koska niitä tapahtuu niin sanotusti, tunnetuimmat kemialliset muutokset.

Muissa reaktioissa on pienempi ΔH, koska ne koostuvat vaihtoehtoisista vaiheista tai vaihtoehtoisista reaktioista samojen tuotteiden saavuttamiseksi D. Siksi ΔH: n summa₁, ΔH₂ ja ΔH₃, Se on yhtä suuri kuin ΔH. Tämän tietäminen, ΔH tai mikä tahansa muu entalpia voidaan laskea soveltamalla yksinkertaisia ​​puhdistuksia. Tämä on Hessin laki.

Hessin laki on erittäin hyödyllinen reaktion entalpiat laskiessasi sekä erilaisten yhdisteiden tai epävakaiden välittäjien entalpiat.

[TOC]

Selitys Hessin laista

Reaktion entalpian laskeminen

Syy, miksi se täyttyy:

ΔH = ΔH₁ + ΔH₂ + ΔH₃

Se johtuu siitä, että entalpia tai entalpian muutos on valtion funktio. Tämä tarkoittaa, että niiden arvoja ei muuteta vaiheiden, vaiheiden tai välittäjäreaktioiden lukumäärällä. Esimerkiksi ΔH pysyy samana, vaikka on ΔH₁₀ Se olisi otettava huomioon algebrallisessa summassa.

Entalplies voitaisiin visualisoida joidenkin vuorten yläosana. Riippumatta siitä, kuinka vaiheet heitä kohti ohjataan, korkeus, joka erottaa ne Mar -tasolta, ei koskaan vaihtele. Ja juuri se on lisätty tai vähennetään ympäröivän vuoren tuntemattoman korkeuden määrittäminen tai vähennetty korkeudet.

Palaa edelliseen kaavioon: A, se on vuori, toisen vuoren ja niin edelleen. Korkeusero A- ja D -yläosien välillä on suurin. Lisäämällä korkeudet A-B: n, B-C: n ja C-D: n välillä, se antaa A-D-korkeuden. Tätä tehdään heidän vastaavien kemiallisten reaktioiden entalpialla.

Voi palvella sinua: fosfaattiryhmä

Reaktion entalpia muodostelmien entalpiat

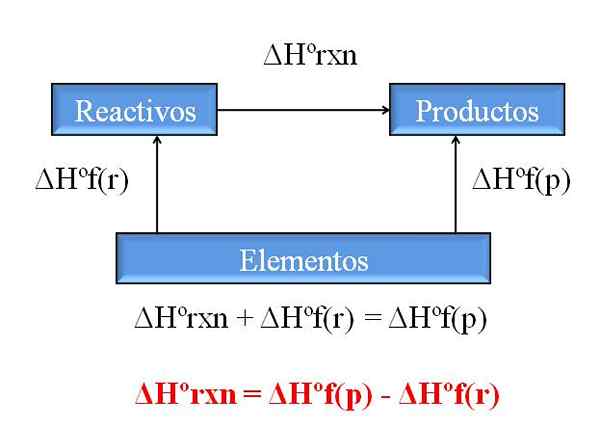Yleinen kaavio reaktion entalpian laskemiseksi muodostelmien entalpiaista. Lähde: Gabriel Bolívar.

Yksi Hessin lain arvokkaimmista seurauksista on, että se sallii minkä tahansa kemiallisen reaktion entalpiat, ottaen kaikkien mukana olevien yhdisteiden (reagenssit ja tuotteet) koulutus entalpikit.

Ylivoimainen kuva kuvaa tätä asiaa. Ymmärretään liittyvän lämmönmuodostuksen entalpia, kun yhdiste muodostuu sen elementeistä. Tästä entalpiasta tulee suurin mahdollinen ero reagenssien ja tuotteiden välillä ilman tarvetta kuulla muita kemiallisia reaktioita; Ainakin yhdisteiden erillisen koulutuksen ulkopuolella.

Kuinka luet kaavion tällä kertaa? Temppu on aina lisätä entalpiat, kun se menee nuolen suuntaan, ja vähennä ne, kun nuoli on vastakkaisella reitillä. Siten ΔHºRXN, tavanomainen reaktion entalpia, lisää ΔHºF (reagenssit), reagenssin muodostumisen tavanomainen entalpia, ja ne vähennetään ΔHºF (tuotteet), tuotteiden muodostumisen tavanomainen entalpia.

Reaktiot summat

Kaavioista voi tulla erittäin monimutkaisia ​​tulkita, varsinkin kun on otettava huomioon monia reaktioita. Siksi reaktioiden summaa käytetään. Tämä menetelmä helpottaa huomattavasti entalpien laskemista ja nopeuttaa Hessin lain ymmärtämistä.

Oletetaan esimerkiksi, että haluat määrittää seuraavan reaktion ΔHºRXN:

A + B + C → ABC

Ja meillä on myös kaksi muuta reaktiota:

A + B → AB (ΔHº₁-A

AB + C → ABC (ΔHº₂-A

On mielenkiintoista, että A + B + C on vasemmalla puolella (reagenssit) ja että ABC on oikealla puolella (tuotteet). Sitten lisäämme vain kaksi viimeistä reaktiota:

A + B → AB

AB + C → ABC

A + AB + C → ABC + AB

Koska AB on molemmilta puolilta, se poistetaan. Ja niin meillä on:

A + B + C → ABC

Δhºrxn = ΔHº₁ + ΔHº₂

Reaktioiden lisääminen minkä tahansa kaavion käyttö jätetään pois.

Hessin lain hakemukset

Hessin laki sallii ilman kokeita, entalpia erilaisille kemiallisille reaktioille tai ilmiöille. Jotkut heistä on lueteltu:

- Epävakaiden yhdisteiden tai välittäjien entalpikien koulutus, kuten yleensä orgaanisessa kemiassa.

-Vaihesiirtymien entalpikit kiteisten kiinteiden aineiden tutkimuksessa.

Voi palvella sinua: kemiallinen yhdiste

-Allotrooppisten siirtymien entalpikit, kuten grafiitin ja timantin välinen.

Samoin Hessin lakia käytetään määrittämään kiinteän aineen retikulaarisen energian ja joidenkin atomien elektroniset affiniteetit.

Esimerkkejä: Ratkaisut harjoitukset

- Esimerkki 1

Laske seuraavan reaktion ΔHrxn:

2HCl (G) + F₂(g) → 2HF (L) + CL₂(g)

Jos sinulla on seuraavat reaktiot ja heidän vastaavat entalpikit:

4HCl (g) + tai₂(g) → 2h₂Tai (l) + 2cl₂(g) (ΔH = -202.4 kJ/mol)

1/2h₂(g) + 1/2f₂(g) → Hf (l) (ΔH = -600.0 kJ/mol)

H₂(g) + 1/2o₂(g) → H₂Tai (l) (ΔH = -285.8 kJ/mol)

Yhtälöiden tilaus

Aluksi meidän on lisättävä reaktiot siten, että HCl ja F₂ ovat vasemmalla puolella ja HF ja Cl₂, Oikealla puolella. Mutta tärkeämpää on, että on huomattava, että niin paljon h₂ h₂Tai eivät ole korkoyhtälön mukaisia. Siksi meidän on peruutettava ne summassa ja annettava stoikiometriset kertoimet samaan aikaan kertolaskuin:

2HCl (g) + 1/2₂(g) → H₂Tai (l) + cl₂(g) (ΔH = -202.4 kJ/mol) * (1/2)

Tämä yhtälö kerrottiin 1/2: lla 2HCl: n sijasta 4HCL: n sijasta

H₂(g) + f₂(g) → 2HF (l) (ΔH = -600.0 kJ/mol) * (2)

Tämä yhtälö kerrottuna 2: lla on F F₂ ja ei 1/2f₂

H₂Tai (l) → H₂(g) + 1/2o₂(g) (ΔH = -285.8 kJ/mol) * (-1)

Sillä välin jälkimmäinen kerrottuna -1: llä "kääntää sen". Siksi meillä on tilattu yhtälöt ja valmis lisäämään.

Yhtälöiden summa

Kaikkien lisääminen antaa meille:

2HCl (g) + 1/2₂(g) → H₂Tai (l) + cl₂(g) (ΔH = -101.2 kJ/mol)

H₂(g) + f₂(g) → 2HF (l) ΔH = -1200.0 kJ/mol)

H₂Tai (l) → H₂(g) + 1/2o₂(g) (ΔH = 285.8 kJ/mol)

2HCl (G) + F₂(g) → 2HF (L) +CL₂(g)

Huomaa, että termit 1/2₂, H₂Tai h₂ Ne peruutetaan, koska ne ovat nuolen molemmilla puolilla. Entalpia lisätään myös, antaen:

Δhrx = 285.8 kJ/mol + (-101.2 kJ/mol) + (-1200.0 kJ/mol)

Tämä ilmaisu on sama kuin alku:

ΔH = ΔH₁ + ΔH₂ + ΔH₃

Ja niin, meillä on, että ΔHRX on yhtä suuri kuin:

Δhrx = -1015.4 kJ/mol

- Esimerkki 2

Tässä esimerkissä nähdään, että vaihtoehtoisten reaktioiden entalpikit vastaavat kiinnostuksen kohteena olevien yhdisteiden muodostumisen entalpioita.

Seuraavaa hajoamisreaktiota varten halutaan määrittää ΔHRXN:

2so₃(g) → 2SO₂(g) + tai₂(g)

Ja SO -yhdisteiden koulutus entalpikit lasketaan käsillä₃ Ja niin₂-

S (s) + o₂(g) → niin₂(g) (ΔH = -296.8 kJ/mol)

Voi palvella sinua: isopreno: rakenne, ominaisuudet, sovellukset

S (s) + 3/2o₂(g) → niin₃(g) (ΔH = -395.6 kJ/mol)

Yhtälöiden tilaus

Tämä harjoitus ratkaistaan ​​samalla tavalla kuin edellinen esimerkki. Sen pitäisi olla niin₃ Ole oikeassa ja kerro 2: lla. Sitä varten meidän on "käännettävä" niin muodostumisyhtälö₃ kertomalla se -1: llä ja sitten kertomalla se 2:

2so₃(g) → 2 s) + 3o₂(g) (ΔH = -395.6 kJ/mol) * (-2)

SO -muodostumisyhtälö₂ Kerroin sen myös 2:

2S (s) + 2₂(g) → 2SO₂(g) (ΔH = -296.8 kJ/mol) * (2)

Yhtälöiden summa

Nyt yhtälöt lisätään:

2so₃(g) → 2 s) + 3o₂(g) (ΔH = 791.2 kJ/mol)

2S (s) + 2₂(g) → 2SO₂(g) (ΔH = -593.6 kJ/mol)

2so₃(g) → 2SO₂(g) + tai₂(g)

Huomaa, että termi 2S poistetaan, koska se on nuolen molemmilla puolilla. Myös kolmas₂ 2o on vähennetty₂ Antaa O₂. Entalpian summa ja siksi ΔHRXN: n arvo on:

ΔH = ΔHrxn = 791.2 kJ/mol + (-593.6 kJ/mol)

= 197.6 kJ/mol

Kuten mikä tahansa hajoamisreaktio, se on endoterminen, joten sen entalpia on positiivinen.

Vaihtoehtoinen menetelmä

On menetelmä, jolla tämä tulos saavutetaan suorana ja yksinkertaisemmalla tavalla. Tämä mainittiin edellisessä osassa.

2so₃(g) → 2SO₂(g) + tai₂(g)

Tämän reaktion ΔHrxn: n määrittämiseksi meidän on laskettava ΔHºF (reagenssit) ja ΔHºF (tuotteet). ΔHºF (niin₃) on yhtä suuri kuin -395.6 kJ/mol, kun taas ΔHºF (niin₂) on yhtä suuri kuin -296.8 kJ/mol. ΔHºF (tai₂) on yhtä suuri kuin 0, koska alkuaine happi on olemassa O: n molekyylinä₂ Eikä atomeja tai vapaa.

Joten meillä on:

ΔHrxn = ΔHºF (tuotteet) - ΔHºF (reagenssit)

= [ΔHºF (niin₂) + ΔHºF (tai₂)] - ΔHºF (niin₃-A

= ΔHºF (niin₂) - ΔHºF (niin₃-A

Meidän on kuitenkin kerrottava molemmat koulutuksen entalpit 2: lla, jotta voidaan sovittaa stökiömetriset kertoimet kemiallisen yhtälön suhteen:

ΔHrxn = 2AHºF (niin₂) - 2AHºF (niin₃-A

Ja laskemalla meillä on:

Δhrxn = 2 (-296.8 kJ/mol) - 2 (-395.6 kJ/mol)

= 197.6 kJ/mol

Itse asiassa tämä on tapa, jolla on yleensä mieluummin ratkaista kaikki harjoitukset, joissa Hess -lakia sovelletaan.

Viitteet

1. Whitten, Davis, Peck & Stanley. (2008). Kemia. (8. ed.-A. Cengage -oppiminen.
2. Wikipedia. (2020). Hessin laki. Haettu: vuonna.Wikipedia.org
3. Cohen Shelly. (18. toukokuuta 2020). Hessin laki. Kemian librettexts. Palautettu: Chem.Librettexts.org
4. Clark Jim. (2010). Hessin laki ja entalpian muutoslaskelmat. Talteenotettu: Chemguide.yhteistyö.Yhdistynyt kuningaskunta
5. Helmestine, Anne Marie, PH.D -d. (11. helmikuuta 2020). Hessin lain määritelmä. Toipunut: Admingco.com
6. Foist Laura. (2020). Hessin laki: Määritelmä, kaava ja esimerkki. Opiskelu. Toipunut: Opiskelu.com
7. Quimitube. (2014). Teoria 14 Thermokemia: Hessin lain reaktion entalpian laskeminen. Palautettu: quimitube.com