Epävakaa tasapainokonsepti ja esimerkit

Mekaniikassa esine on Epävakaa tasapaino Kun siirtämällä sitä vain asennosta voimalla, se ei palaa siihen. Esimerkiksi seuraavan kuvan pallo, kun se on kukkulan yläpuolella, on epävakaa tasapainossa, koska pienin häiriö tekee siitä ylösalaisin ilman mahdollisuutta palata omalla keinolla.

Kuvio 1. Pallo on epävakaassa tasapainossa vasemman asennossa, välinpitämättömässä tasapainossa keskellä ja vakaassa tasapainossa oikealle. Lähde: Wikimedia Commons.

Toisaalta, kun pallo on tasaisella pinnalla, kuten keskuksen asennossa, sanotaan, että se on välinpitämätön tasapaino tai neutraali. Sitä häiritsevä voima voidaan kohdistaa, siirtämällä se toiselle puolelle, mutta jos voima katoaa, pallo on jälleen vakaa.

Lopuksi, oikealla, pallo on koveran kulhon pohjassa. Tämä asema on myös tasapainossa, mutta tasapaino. Palloa häiritsevä voima saa sen vain heilahtamaan hiukan alkuperäisen asennon ympärillä, lopulta palaamaan siihen.

[TOC]

Tasapainon menetyksen syyt

Yleiset esineet (ja ihmiset ja eläimet) menettävät tasapainonsa ja putoamassa painosta johtuvan vääntömomentin takia, maapallon asettama voima kaikkien pinnan lähellä olevien esineiden yli. Kun sinulla on pidennetty runko, kohta, jossa painotoimia kutsutaan painovoima.

Paino voi olla tasapainossa tuen ansiosta, kuten se, joka tarjoaa pinnan, ja tällä tavalla esine ei liiku. Mutta silti on mahdollisuus kääntyä johonkin kohtaan, koska laajennetuissa esineissä voimien tasapaino ei ole ainoa tekijä, joka pitää ne edelleen, vaan myös paikka, jossa näitä voimia käytetään.

Alla on luku, jonka kärjessä on tasapainoinen lyijykynä, epävakaa tasapaino. Mikä tahansa ilmavirta kääntää sen pois, mutta sillä välin itse tukeva normaali paino ja voima korvataan. Lisäksi molemmilla voimilla on sama toimintalinja ja tämä kulkee lyijykynän kärjen läpi, varmistaen tasapainon.

Voi palvella sinua: Ei -koplanarvektorit: Määritelmä, olosuhteet, harjoitukset

Mutta jos lyijykynä nojaa vain vähän, kuten oikealla osoitetaan, painon toimintalinja lakkaa kulkevan kärjen läpi, joka toimii nivelnäytteenä. Sitten paino tuottaa tasapainoisen vääntömomentin ja lyijykynä pyörii kellon käsien suuntaan.

Kuva 2. Sen kärjessä tuettu lyijykynä on epävakaassa tasapainossa, pieni häiriö aiheuttaa painon tuottaa vääntömomentin kärjen suhteen ja lyijykynä putoaa. Lähde: f. Zapata.

Stabiilisuuden takaavat tekijät

Melkein aina sitä, mitä etsitään, on vakaa tasapaino, koska epävakaa tasapaino on, kuten sen nimi osoittaa, melko epävarma. Jatkamalla lyijykynän esimerkkiä, kun se putoaa ja pysyy vaakasuorassa pinnalla, uusi sijainti on paljon vakaampi kuin silloin, kun se pysäytettiin kärjessä.

Tämä johtuu siitä, että toisaalta painopiste on lähempänä pintaa ja toisaalta kynän tukipinta on paljon suurempi.

Kun tukipinta on Lar. Ja jos etäisyys painopisteestä pintaan on alhaisempi, painovivun käsivarsi on alhaisempi, ja siksi vääntömomentti on myös.

Yhteenvetona voidaan todeta, että mitä suurempi esineen tuen perusta on ja lähempänä sen painovoimaa lattialle, sitä vähemmän kaatumisen todennäköisyys ja tasapaino on yleensä vakaa. Vauvat tietävät sen, ja siksi he yleensä murtavat ensin ennen kuin riskivät seisomaan.

Ja jos sen sijaan, että tuetaan, vartalo ripustetaan pisteestä, painopisteen sijainti on myös merkittävä rooli tasapainon luomisessa, kuten pian seuraavissa esimerkeissä nähdään.

Voi palvella sinua: Mount Olympus (Mars)

Tasapainottaa esimerkkejä

Tuetujen elimien tasapaino

Tuettujen elinten tasapaino riippuu, kuten todettiin:

-Kuinka lähellä pinnan painopiste.

-Objektin pohjan koko.

Harkitse kartiota tasaisella pöydällä. Vakain sijainti epäilemättä on kartion pohjan tuettu täysin pöydällä. Tämä on vakaa tasapainon sijainti, koska kartion painopiste on symmetrian akselilla ja lähempänä sen pohjaa kuin kärkeä.

Välinpitämätön tasapaino saavutetaan asettamalla kartio valehtelemaan ja epävakaa tasapaino vastaa sen kärjessä olevaa kartiota, kuten lyijykynä, joka ei ehkä ole helppo tehtävä, kun otetaan huomioon, että pienin liike, jonka kartio kääntyy.

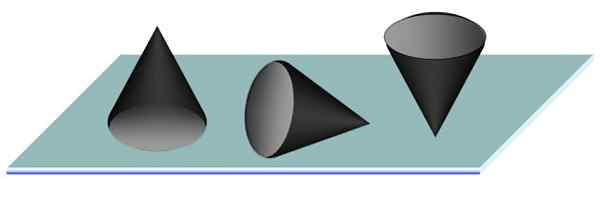Kuva 3. Taulukossa tuetun kartion vakaa, välinpitämätön ja epävakaa tasapaino. Lähde: f. Zapata.

Tasapaino ripustetuissa elimissä

On yleistä löytää ripustettuja kappaleita, jotka ripustavat ainakin yhden pisteen, kuten maalaukset ja lamput. Tasapainon määrittämisessä on tarpeen harkita painopisteen ja suspensiopisteen sijaintia.

Tilanne on helppo visualisoida suorakaiteen muotoisen pahvilevyn tai homogeenisen materiaalisen säännön avulla. Tässä painopiste on samanaikaisesti kuvan geometrisen keskuksen kanssa, olettaen, että esineen massa on jakautunut tasaisesti.

Arkin asettamiseksi epävakaaseen tasapainoon se ripustetaan löydetystä pisteestä alla Painovoiman keskipisteestä se pitää vain arkin sormien välillä kiristämättä liikaa, jättääkseen hänelle liikkumisvapauden.

Pieni voima riittää, jotta arkki pyörii heti tietyssä mielessä. Syynä käännökseen on sama kuin tuetun esineen tapauksessa: paino käyttää thromplorgal -vääntömomenttia, joka helpottaa kehon pyörimistä.

Voi palvella sinua: Ratkaisu Heat: Kuinka se lasketaan, sovellukset ja harjoitukset

Kun kääntyy, arkki kulkee vakaan tasapainon asennon läpi, jossa suspensiopiste pysyy ylhäältä painopiste. Tämän aseman ympärillä se vaihtelee vähän ja lopulta pysähtyy.

Jos voima kohdistetaan uudelleen, lamina vaihtelee jälleen, mutta palaa uudelleen siihen asentoon, jossa suspensio ja painopiste kohdistuvat pystysuoraan.

Lopuksi välinpitämätön tasapaino tarkistetaan siirtämällä tappi tarkasti painopisteen läpi. Jos arkki käännetään pysymään eri asentoissa, nähdään, että niiden välillä ei ole suurempaa eroa.

Yhteenvetona voidaan todeta, että epävakaassa tasapainossa ripustetuille ruumiille suspensio on painopisteen alapuolella. Ja päinvastoin vakaan tasapainon suhteen.

Viitteet

1. Bauer, W. 2011. Fysiikka tekniikkaan ja tieteisiin. Osa 1. MC Graw Hill.
2. Giancoli, D.  2006. Fysiikka: sovellusten periaatteet. Kuudes. Ed Prentice Hall.
3. Hewitt, Paul. 2012. Käsitteellinen fysiikka. Viides. Ed. Pearson.
4. Resnick, r. (1999). Fyysinen. Osa. 1. 3. ed. espanjaksi. Mannertoimitusyhtiö S.-Lla. C: n.V.
5. Rex, a. 2011. Fysiikan perusteet. Pearson.
6. Sears, Zemansky. 2016. Yliopiston fysiikka, jolla on moderni fysiikka. 14. päivä. Ed. Osa 1. Pearson.