Lämpötasapainoyhtälöt, sovellukset, harjoitukset

Kahden lämpökontaktissa olevien kappaleiden lämpötasapaino on tila, joka saavutetaan riittävän pitkän ajan jälkeen, jotta molempien kappaleiden lämpötilat ovat yhtä suuret kuin.

Termodynamiikassa kahden kappaleen (tai kahden termodynaamisen järjestelmän) lämpökontaktissa ymmärretään tilanteena, jossa rungoilla on mekaaninen kosketus tai ne on erotettu, mutta kosketuksessa pinnan kanssa, joka sallii vain lämmönkulun ruumiista toiseen (Diaterinen pinta -A.

Kuvio 1. Jonkin ajan kuluttua jää ja juoma saavuttavat heidän lämpötasapainonsa. Lähde: Pixabay

Lämpökosketuksessa kosketussa olevien järjestelmien välillä ei pitäisi olla kemiallista reaktiota. Lämmönvaihtoa pitäisi olla vain.

Jokapäiväiset tilanteet, joissa lämmönvaihto on olemassa, esitetään järjestelmillä, kuten kylmäjuoma ja lasi, kuuma kahvi ja teelusikallinen, runko ja lämpömittari, monien muiden esimerkkien joukossa.

[TOC]

Kun kaksi tai useampi järjestelmä on lämpötasapainossa?

Termodynamiikan toinen laki osoittaa, että lämpö siirtyy aina korkeimmasta lämpötilan rungosta alhaisimpaan lämpötilaan. Lämmönsiirto lakkaa heti, kun lämpötilat tasoitetaan ja lämpötasapainon tila saavutetaan.

Lämpötasapainon käytännöllinen käyttö on lämpömittari. Lämpömittari on laite, joka mittaa oman lämpötilansa, mutta lämpötasapainon ansiosta voimme tietää muiden kappaleiden lämpötilan, kuten ihmisen tai eläimen lämpötilan.

Elohopeapylväslämpömittari asetetaan lämpökontaktiin rungon kanssa, esimerkiksi kielen alla, ja riittävän ajan odotetaan saavuttavan kehon ja lämpömittarin välinen lämpötasapaino ja että sen lukeminen ei vaihtele enemmän.

Kun tämä kohta saavutetaan, lämpömittarin lämpötila on sama kuin runko.

Termodynamiikan nolla -laki osoittaa, että jos runko A on lämpötasapainossa, jossa on rungon C ja sama runko C on lämpötasapainossa B: n kanssa, niin A ja B ovat lämpötasapainossa, vaikka A: n ja B: n välillä ei ole lämpökontaktia.

Johtopäätöksenä on, että kaksi tai useampi järjestelmä on lämpötasapainossa, kun niillä on sama lämpötila.

Lämpötasapainoyhtälöt

Oletamme, että rungon alkulämpötilassa lämpökontaktissa toisen B -rungon kanssa, jolla on alkulämpötila TB. Oletetaan myös, että Ta> TB, sitten toisen lain mukaan lämpö siirretään A: sta b.

Jonkin ajan kuluttua lämpötasapaino saavutetaan ja molemmilla kappaleilla on sama lopullinen lämpötila TF. Tällä on väliarvo TA: lle ja TB: lle, ts. TA> tf> TB.

A: sta B: stä B: stä siirretyn lämmön määrä on qa = ma ca (tf - ta), missä MA on kehon A, Ca, lämpökapasiteetti y (tf - ta) lämpötilaerot. Jos TF on pienempi kuin, QA on negatiivinen, mikä osoittaa, että vartalo antaa lämpöä.

Samoin keholle B sinun täytyy QB = MB CB (TF - TB); Ja jos TF on suurempi kuin TB, QB on positiivinen, mikä osoittaa, että vartalo B vastaanottaa lämpöä. Koska runko A ja B ovat lämpökontaktissa niiden välillä, mutta ympäristöstä eristettynä, vaihdetun lämmön kokonaismäärän tulisi olla nolla: QA + QB = 0

Sitten ma ca (tf - ta) + mb cb (tf - tb) = 0

Tasapainotuslämpötila

Tämän ekspression kehittäminen ja TF -lämpötilan puhdistaminen saadaan lopullinen lämpötasapainon lämpötila.

Kuva 2. Lopullinen tasapainolämpötila. Lähde: Itse tehty

Tf = (ma ca ta + mb cb tb) / (ma ca + mb cb).

Tietyssä tapauksessa harkitse tapausta, että rungot A ja B ovat identtisiä massassa ja lämpökapasiteetissa, tässä tapauksessa tasapainolämpötila on:

Tf = (ta + tb) / 2 ↔ Jos MA = MB ja CA = CB.

Lämpökosketus vaihemuutoksen kanssa

Joissakin tilanteissa tapahtuu, että kun kaksi kappaletta asetetaan lämpökontaktiin, lämmönvaihto aiheuttaa tilan tai vaiheen muutoksen yhdessä niistä. Jos näin tapahtuu, on otettava huomioon, että vaihemuutoksen aikana kehossa ei ole lämpötilan muutosta, joka muuttaa sen tilaa.

Jos tapahtuu yhden kehon vaihemuutos lämpökontaktissa, käytetään piilevän lämmön L käsitettä, joka on valtion muutoksen välttämätön massayksikköä kohti:

Q = l ∙ m

Esimerkiksi 1 kg: n jäätä 0 ° C: ssa, vaaditaan 333,5 kJ/kg ja tämä arvo on jäähaunan piilevä lämpö.

Fuusion aikana kiinteä vesi muutetaan nestemäiseksi vedeksi, mutta vesi ylläpitää samaa jäälämpötilaa sulautumisprosessin aikana.

Sovellukset

Lämpötasapaino on osa jokapäiväistä elämää. Esimerkiksi, tutkitaan tätä tilannetta yksityiskohtaisesti:

-Harjoitus 1

Henkilö haluaa uida lämpimällä vedellä 25 ° C: ssa. Kuutiossa 3 litraa kylmää vettä 15 ° C: ssa ja keittiön lämpöä vettä jopa 95 ° C: seen.

Kuinka monta litraa kuumaa vettä on lisättävä kylmän veden kuutioon halutun lopullisen lämpötilan saamiseksi?

Ratkaisu

Oletetaan, että se on kylmää vettä ja b kuumaa vettä:

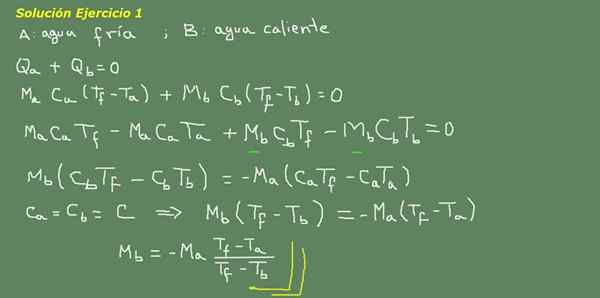Kuva 3. Harjoitus 3 -ratkaisu. Lähde: Itse tehty.

Ehdotamme lämpötasapainoyhtälöä, kuten kuvion 3 pöydällä on osoitettu ja sieltä puhdistamme MB -veden.

Alkuperäinen kylmän veden massa voidaan saada, koska veden tiheys tunnetaan, mikä on 1 kg jokaiselle litralle. Eli meillä on 3 kg kylmää vettä.

MA = 3 kg

Niin

MB = - 3 kg*(25 ° C - 15 ° C)/(25 ° C - 95 ° C) = 0,43 kg

Sitten riittää 0,43 LT: llä kuumaa vettä lopulta 3,43 litraa lämpimää vettä 25 ° C: ssa.

Ratkaisut

-Harjoitus 2

Pala metalli 150 g massaa otetaan käyttöön ja 95 ° C: n lämpötilassa säiliöön, joka sisältää puoli litraa vettä lämpötilassa 18 ° C. Jonkin ajan kuluttua lämpötasapaino ja veden ja metallin lämpötila ovat 25 ° C.

Oletetaan.

Hanki metallin spesifinen lämpö.

Ratkaisu

Ensin laskemme veden absorboiman lämmön:

QA = ma ca (TF - TA)

QA = 500 g 1cal/(g ° C) (25 ° C - 18 ° C) = 3500 kaloria.

Se on sama metalli antaa:

QM = 150 g cm (25 ° C - 95 ° C) = -3500 kaloreita.

Sitten voimme saada metallin lämpökapasiteetin:

Cm = 3500 cal/ (150 g 70 ° C) = ⅓ cal/ (g ° C).

Harjoitus 3

Sinulla on 250 c.c. vettä 30 ° C: ssa. Tähän veteen, joka on eristävässä termossa, lisätään 25 g jääkuutiota 0 ° C.

Määritä tasapainolämpötila; toisin sanoen lämpötila, joka pysyy, kun kaikki jää on sulanut ja jäävesi on lämmitetty, kunnes vesi, jolla oli alun perin lasi.

Ratkaisu 3

Tämä harjoitus voidaan ratkaista kolmessa vaiheessa:

1. Ensimmäinen on jään fuusio, joka imee lämpöä alkuperäisestä vedestä sulamaan ja tulemaan veteen.
2. Sitten lasketaan alkuperäisen veden lämpötilan laski, koska se on antanut lämpöä (QCED<0) para fundir el hielo.
3. Lopuksi sulaa vettä (jäästä) on oltava termisesti tasapainossa alun perin olemassa olevan veden kanssa.

Kuva 4. Harjoitus 3 -ratkaisu. Lähde: Itse tehty.

Lasketaan jäätelön fuusioon tarvittava lämpö:

Qf = l * mh = 333,5 kJ/kg * 0,025 kg = 8,338 kJ

Sitten veden määräämä lämpö jään sulamiseksi on QCED = -QF

Tämä veden määräämä lämpö laskeutuu lämpötilan arvoon, jonka voimme laskea seuraavasti:

T '= t0 - qf/(ma*ca) = 22,02 ° C

Missä CA on veden lämpökapasiteetti: 4,18 kJ/(kg ° C).

Lopuksi alkuperäinen vesimassa, joka on nyt 22,02 ° C: ssa, tuottaa lämmön sulaan veteen jäästä, joka on 0 ° C: ssa.

Lopuksi tasapainolämpötila saavutetaan tarpeeksi ajan kuluttua:

TE = (ma * t ' + mh * 0 ° C) / (ma + mh) = (0,25 kg * 22,02 ° C + 0,025 kg * 0 ° C) / (0,25 kg + 0,025 kg)).

Lopuksi tasapainolämpötilan hankkiminen:

TE = 20,02 ° C.

-Harjoitus 4

0,5 kg: n lyijykappale jättää uunin lämpötilassa 150 ° C, joka on aivan sen sulamispisteen alapuolella. Tuo pala on asetettu astiaan, jossa on 3 litraa vettä huoneenlämpötilassa 20 ° C. Määritä lopullinen tasapainolämpötila.

Laske myös:

- Lyijyn toimittaman lämmön määrä vettä.

- Veden absorboivan lämmön määrä.

Tiedot:

Erityinen lyijylämpö: CP = 0,03 kalkki/(g ° C); Erityinen vesilämpö: Ca = 1 kalkki/(g ° C).

Ratkaisu 

Ensinnäkin määritämme lopullisen tasapainon lämpötilan te:

TE = (ma ca ta + mp cp tp) / (ma ca + mp cp)

TE = 20,65 ° C

Sitten lyijyn määrittämä lämmön määrä on:

Qp = mp cp (TE - tp) = -1,94 x 10³ kalkki.

Veden absorboivan lämmön määrä on:

QA = MA CA (TE - TA) = +1,94x 10³ Lime.

Viitteet

1. Atkins, p. 1999. Fysikaalinen kemia. Omega -versiot.
2. Bauer, W. 2011. Fysiikka tekniikkaan ja tieteisiin. Osa 1. MC Graw Hill.
3. Giancoli, D. 2006. Fysiikka: sovellusten periaatteet. 6. ... Ed Prentice Hall.
4. Hewitt, Paul. 2012. Käsitteellinen fysiikka. Viides. Ed. Pearson.
5. Resnick, r. (1999). Fyysinen. Osa. 1. 3. ed. espanjaksi. Mannertoimitusyhtiö S.-Lla. C: n.V.
6. Rex, a. 2011. Fysiikan perusteet. Pearson.
7. Sears, Zemansky. 2016. Yliopiston fysiikka, jolla on moderni fysiikka. 14. päivä. Ed. Osa 1.
8. Serway, R., Jewett, J. (2008). Fysiikka tieteen ja tekniikan fysiikka. Osa 1. Seitsemäs. Ed. Cengage -oppiminen.