Satunnainen virhekaava ja yhtälöt, laskelmat, esimerkit, harjoitukset

Hän satunnainen virhe fyysinen määrä koostuu kyseisen määrän mittaamattomista muunnelmista. Nämä variaatiot voivat tuottaa ilmiö, joka mitataan mittauslaitteella tai itse tarkkailijalla.

Tällainen virhe ei johdu siitä tosiasiasta, että jotain on tehty väärin kokeen aikana, vaan että se on mittausprosessissa tai tutkittu ilmiö. Tämä aiheuttaa mitatun mittauksen joskus hiukan suuremman ja joskus hiukan alhaisemman, mutta yleensä heilahtelee keskusarvon ympärillä.

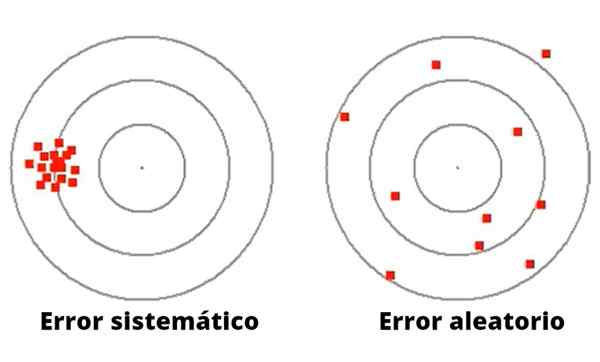
Kuvio 1- Satunnaisvirheet vaihtelevat suuruudessa ja suunnassa. Päinvastoin, systemaattiset virheet ovat yleensä johdonmukaisia.

Toisin kuin satunnaisvirhe, systemaattinen virhe voi johtua huonosta kalibroinnista tai mittauslaitteessa sopimattomasta asteikon tekijästä, mukaan lukien vika kokeellisissa laitteissa tai sopimattoman havainnon, joka aiheuttaa poikkeaman samassa mielessä.

Kuvio 1 kuvaa eroa systemaattisen ja satunnaisen virheen välillä DART -käynnistyspelissä tavoitteeseen ympyröillä.

Vasen tapauksessa tikkat ovat keskittyneet hyvin kaukana keskustasta. Näiden tikankan syöttäjällä, vaikkakin hyvällä tavoitteella, on systemaattinen vika, ehkä visuaalinen alku.

Toisaalta oikealla olevalla syöttäjällä (kuvassa 1) on suuri hajonta keskuskohteen ympärille, siksi se on erittäin epätarkka syöttäjä, jolla on huono tavoite, mikä tekee tahattomasti satunnaista virhettä.

[TOC]

Kaavat ja yhtälöt satunnaisessa virheessä

Kun mittausprosessi näyttää satunnaisen virheen, se on välttämätöntä.

Tietenkin, jokaisessa mittauksessa on tarpeen huolehtia siitä, että ne toteutettavissa olosuhteet ovat aina samat.

Voi palvella sinua: Faradayn laki: kaava, yksiköt, kokeet, liikunta,

Oletetaan, että mittaus toistetaan n ajat. Koska kussakin mittauksessa on satunnaista virhettä, se on hiukan erilainen arvo. Oletetaan n Mittaukset ovat:

x₁, x₂, x₃,…, X_n

Joten mikä arvoraportti mittauksesta? 

Keskiarvo ja keskihajonta

Se keskiarvo jompikumpi keskiverto toimenpiteistä, jotka merkitsemme ja lasketaan seuraavasti:

= (x₁ + x₂ + x₃ +… +X_n) / n

Keskihajonta

Tällä tuloksella on kuitenkin keskihajonnan antama virhemarginaali. Sen määrittelemiseksi sinun on ensin tiedettävä poikkeama ja sitten varianssi:

-Poikkeama d -d_Yllyttää  että jokaisella mitatulla arvolla on Xi Keskimääräisen arvon suhteen on:

d -d_Yllyttää = x_Yllyttää -

Jos poikkeamien keskiarvo lasketaan, se saadaan systemaattisesti = 0, olettaen että: 

= (D₁ + d -d₂ + d -d₃ +… +D_n) /n =

= [x₁ - ) + (x₂ - ) +… +(X_n - )/n

= (x₁+ x₂ +… + X_n) / n - n / n = - = 0

-Poikkeamien keskiarvo ei ole hyödyllistä tietää toimenpiteiden leviäminen. Toisaalta poikkeamien tai varianssin neliön keskiarvo, jonka merkitsee σ², kyllä ​​se on.

Se lasketaan seuraavan kaavan mukaan:

σ² = (D₁² + d -d₂² +.. .+ d -d_n² ) / (N -1)

Tilastoissa tätä määrää kutsutaan varianssi.  

Ja sen varianssin neliöjuuressa se tunnetaan nimellä Keskihajonta σ-

σ = √ [(D₁² + d -d₂² +.. .+ d -d_n² ) / (n -1)] 

Vakiopoikkeama σ osoittaa, että:

1.- 68% tehdyistä mittauksista sisältyy aikaväliin [ - σ, + σ]. 

2.- 95% mittauksista on aikavälillä [ - 2σ, + 2σ].

3.- 99,7% toteutetuista toimenpiteistä on alueella [ - 3σ, + 3σ].

Kuinka laskea satunnainen virhe?

Mittaustulos on keskiarvo niistä n Mittaukset, jotka on merkitty ja lasketaan seuraavan kaavan mukaan:

Voi palvella sinua: areolaarinen nopeus: miten se lasketaan ja ratkaistu harjoitukset

= (∑x_Yllyttää) / n

Se ei kuitenkaan ole mittauksen "tarkka" arvo, koska siihen vaikuttaa siihen Satunnainen virhe ε, joka on laskettu näin:

ε = σ / √n

Missä:

σ = √ [(∑ (xi -)² ) / (n -1)]

Mittauksen lopputulos on ilmoitettava millä tahansa seuraavista tavoista:

1. ± σ / √n = ± ε 68%: n luottamustasolla.
2. ± 2σ / √n = ± 2ε 95%: n luottamustasolla.
3. ± 3σ / √n = ± 3ε 99,7%: n luottamustasolla.

Satunnainen virhe vaikuttaa mittauksen viimeiseen merkittäviin lukuihin, jotka yleensä vastaavat mittauslaitteen arviointia. Jos satunnainen virhe on kuitenkin erittäin suuri, variaatio voi vaikuttaa kahteen viimeiseen merkittävään numeroon.

Satunnaiset virheesimerkit

Satunnaiset virheet voivat esiintyä useissa tapauksissa, joissa mitta tehdään:

Pituuden mittana mittanauhalla tai sääntöllä

Kun pituus mitataan säännöllä tai mittanauhalla ja lukemat putoavat asteikon tuotemerkkien välillä, niin väliarvo arvioidaan.

Joskus arviolla on ylimääräinen ja muu vika, joten mittausprosessiin tehdään satunnaista virhettä.

Kuva 2. Satunnaiset virheet voivat näkyä, kun pituus mitataan nauhateipillä. Lähde: Pikrepo.

Tuulen nopeus

Tuulen nopeuden mittaamisessa lukemisessa hetkestä toiseen voi tapahtua muutoksia ilmiön muuttuvan luonteen vuoksi.

Kun luet äänenvoimakkuutta valmistuneessa sylinterissä

Kun tilavuus luetaan asteittaisella sylinterillä, jopa yrittäen minimoida rinnakkaisuusvirheen, joka kerta kun se mitataan, meniscal -havaintokulma muuttuu hiukan, minkä vuoksi satunnainen virhe vaikuttaa mittauksiin.

Se voi palvella sinua: Ensimmäinen tasapainotila: Selitys, esimerkit, harjoitukset Kuva 3.- Kemian laboratoriossa on mahdollista tehdä satunnaisia ​​virheitä jatko -sylinterin lukemisessa. Lähde: Pexels.

Kun lapsen asema mitataan

Mittaamalla lapsen korkeus, varsinkin jos se on vähän levoton, se saa pienet asennot muuttumaan hieman lukemaan.

Kun käytät kylpyhuoneen asteikkoa

Kun haluamme mitata painomme kylpyhuoneessa, pieni muutos tukipisteessä, jopa aseman muutos voi satunnaisesti vaikuttaa mittaukseen.

Liikuntaa

Lelulottarin annetaan rullata suoraa ja kaltevaa rataa pitkin ja mitataan sekuntikellolla, joka vie koko radan. 

Mittaus tehdään 11 ​​kertaa, huolellisesti vapauttaa kärry samasta paikasta antamatta mitään impulssia ja pitämällä kaltevuuskorjaukset.

Saatujen tulosten joukko on:

3,12s 3,09s 3,04s 3,04s 3,10s 3,08s 3,05s 3,10s 3.11s 3,06s, 3,03s

Mikä on mittojen satunnainen virhe?

Kuva 4. Ottaen lelulelun ajan, joka laskeutuu kaltevan tason läpi. Lähde: Fanny Zapata.

Ratkaisu

Kuten voidaan nähdä, saadut tulokset eivät ole ainutlaatuisia ja vaihtelevat hieman.

Ensimmäinen on laskea keskimääräinen laskeutumisajan arvo, saadaan 3,074545455 sekuntia.

Ei ole mitään järkeä ylläpitää niin monia desimaaleja, koska jokaisella mittauksella on kolme merkittävää lukua ja kunkin toimenpiteen toinen desimaali on epävarma, koska se on sekuntikellon arvostamisraja, joten tulos on pyöristetty kahteen desimaaliin:

= 3,08 s.

Laskimen ollessa tilastollisessa tilassa keskihajonta on σ = 0,03 s Ja vakiovirhe on σ / √11 = 0,01 s. Lopputulos ilmaistaan ​​seuraavasti:

Laskeutumisaika 

3,08 s ± 0,01 s (68%: n luottamustasolla)

3,08 s ± 0,02 s (95%: n luottamustasolla)

3,08 s ± 0,03 s (99,7%: n luottamustasolla)

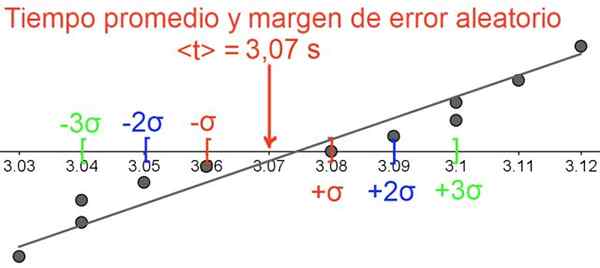Kuva 5. Satunnainen virhemarginaali, huomaa, että tiedot on ryhmitelty keskiarvoon. Lähde: f. Zapata.

Viitteet

1. Canavos, G. 1988. Todennäköisyys ja tilastot: Sovellukset ja menetelmät. McGraw Hill.
2. DeVore, J. 2012. Tekniikan ja tieteen todennäköisyys ja tilastot. Kahdeksas. Painos. Kyynärmä.
3. Helmestiina a. Satunnainen virhe vs. Systemaattinen virhe. Toipunut: Admingco.com
4. Laredo, E. Keskivirheet. Toipunut: USB.mennä.
5. Levin, r. 1988. Järjestelmänvalvojien tilastot. Toinen. Painos. Prentice Hall.