Käänteiset trigonometriset toiminnot, johdetut, esimerkit, harjoitukset

Se Käänteiset trigonometriset toiminnot, Kuten nimestä voi päätellä.

Käänteiset trigonometriset funktiot merkitään sen vastaavan suoran trigonometrisen toiminnon samalla nimellä sekä etuliite Kaari. Täten:

1.- Arcsen (x) Se on funktion käänteinen trigonometrinen funktio synti (x)

2.- Arccos (x) Se on funktion käänteinen trigonometrinen funktio cos (x)

3.- Arctan (x) Se on funktion käänteinen trigonometrinen funktio Tan (x)

4.- Arccot ​​(x) Se on funktion käänteinen trigonometrinen funktio pinnasänky (x)

5.- Arcsec (x) Se on funktion käänteinen trigonometrinen funktio Sec (x)

6.- ARCCSC (x) Se on funktion käänteinen trigonometrinen funktio CSC (x)

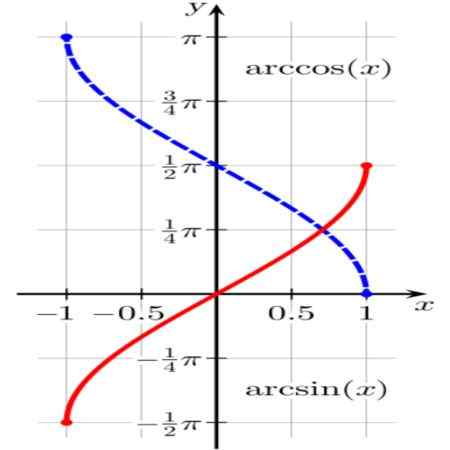
Kuvio 1. Arcsen -toiminnot (x) (punaisella) ja arccos (x) (sinisellä). Lähde: Wikimedia Commons.

Toiminto θ = Arcsen (x) Se johtaa yksikkökaariin θ (tai kulma radianeissa θ) sellainen sin (θ) = x.

Siten esimerkiksi Arcsen (√3/2) = π/3 Koska kuten tiedetään, π/3 radiaanien rinta on yhtä suuri kuin √3/2.

[TOC]

Käänteisten trigonometristen funktioiden pääarvo

Niin, että matemaattisella funktiolla F (x) on käänteinen g (x) = f^-1(x) On välttämätöntä, että tämä toiminto on Injektiivinen, Mikä tarkoittaa, että funktion f (x) jokainen arvo ja saapumisjoukko tulee vain yhdestä x -arvosta.

On selvää, että mikään trigonometrinen funktio ei täytä tätä vaatimusta. Huomaa, että pisteen selventäminen, että arvo y = 0,5 voidaan saada sinusfunktiosta seuraavilla tavoilla:

• sin (π/6) = 0,5
• synti (5π/6) = 0,5
• synti (7π/6) = 0,5

Ja monia muita, koska sinusfunktio on jaksollinen ajanjaksolla 2π.

Se voi palvella sinua: Monilaitteet 8: mitä ovat ja selitys

Käänteisten trigonometristen funktioiden määrittelemiseksi on välttämätöntä rajoittaa niiden vastaavien suorien trigonometristen toimintojen alue, jotta ne täyttävät injektiivisuusvaatimukset.

Tämä suoran toiminnan rajoitettu alue on vastaavan käänteisen toiminnan pääalue tai haara.

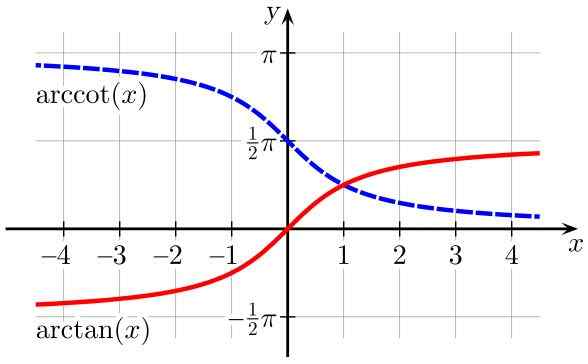Kuva 2. Arctan -toiminnot (x) (punaisella) ja arccot ​​(x) (sinisellä). Lähde: Wikimedia Commons.

Taulukko verkkotunnuksista ja käänteisten trigonometristen funktioiden alueista

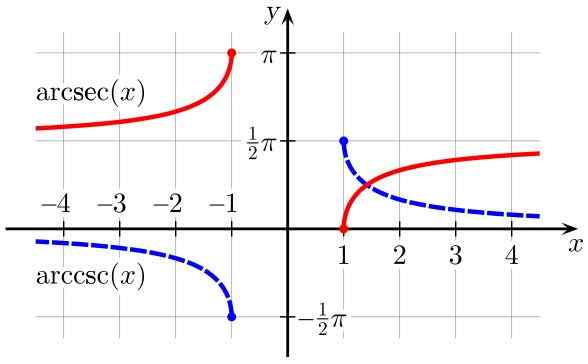Kuva 3. Arcsec (x) (punaisella) ja arccsc (x) (sinisellä) funktiot (sinisellä). Lähde: Wikimedia Commons.

Johdettu käänteisistä trigonometrisista toiminnoista

Käänteisten trigonometristen funktioiden johdannaisten saamiseksi käytetään johdannaisten ominaisuuksia, erityisesti käänteisestä toiminnasta johdettuja ominaisuuksia.

Jos merkitsemme f (y) funktioon ja f^-1(x) käänteisfunktioon, sitten johdettu käänteisestä funktiosta liittyy suoran toiminnan johdannaiseen seuraavan suhteen kautta:

[F^-1(x)] '= 1/ f' [f^-1(x)]

Esimerkiksi: Jos x = f (y) = √y on suora funktio, sen käänteinen on

y = f^-1(x) = x². Käytämme käänteisen johdannaisen sääntöä tähän yksinkertaiseen tapaukseen nähdäksesi, että tämä sääntö on täytetty:

[x²] '= 1 / [√y]' = 1 / (½ ja^-½ = 2 ja^½ = 2 (x²-A^½ = 2x 

No, voimme arvioida tämän tempun löytääksemme ne, jotka on johdettu käänteisistä trigonometrisistä toiminnoista.

Esimerkiksi otamme θ = Arcsen (x) Suorana funktiona sen käänteinen toiminta on sin (θ) = x.

[Arcsen (x)] '= 1 / [sin (θ)]' = 1 / cos (θ) = 1 / √ (1 - sen (θ)²) =…

… = 1 / √ (1 - x²-A .

Tällä tavoin voidaan saada kaikki käänteisistä trigonometrisistä funktioista johdetut, jotka on esitetty alla:

Kuva 4. Taulukko niistä, jotka on johdettu käänteisistä trigonometrisistä funktioista. Lähde: Wikimedia Commons.

Nämä johdannaiset ovat voimassa kaikissa monimutkaisissa numeroissa oleviin z -argumenteihin, ja siksi ne ovat voimassa myös kaikissa todellisissa argumenteissa X, koska z = x + 0i.

Voi palvella sinua: nelikulmainen: elementit, ominaisuudet, luokittelu, esimerkit

Esimerkit

- Esimerkki 1

Löydä arctan (1).

Ratkaisu

Arktan (1) on yksikkökaari (kulma radianeissa) ፀ siten, että tan (ፀ) = 1. Tuo kulma on ፀ = π/4, koska niin (π/4) = 1. Sitten arktan (1) = π/4.

- Esimerkki 2

Laske arcsen (cos (π/3)).

Ratkaisu

Kulma π/3 radiaanit ovat merkittävä kulma, jonka kosini on ½, niin että ongelma pelkistetään Arcsenin (½) löytämiseen (½).

Joten kyse on kulman löytämisestä, jonka sini antaa ½. Tämä kulma on π/6, koska sen (π/6) = sen (30º) = ½. Siksi Arcsen (cos (π/3)) = π/6. 

Harjoitukset

- Harjoitus 1

Etsi seuraavan lausekkeen tulos:

Sec (Arcan (3)) + CSC (Arccot ​​(4))

Ratkaisu

Alamme nimetä α = Arcan (3) ja β = Arcot (4). Joten lauseke, joka meidän on laskettava, on tällainen:

SEC (α) + CSC (β)

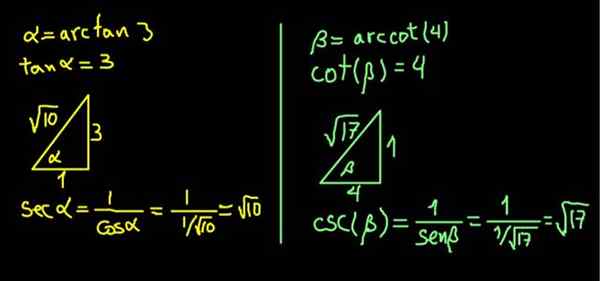
Ekspressio α = Arcan (3) vastaa niin sanoista (α) = 3.

Koska tangentti on viereisen vastakkaisen jalka, rakennetaan 3 yksikön a ja viereinen luokka, joka vastustaa Catoton suorakulmiokolmiota, ja se (α) = 3/1 = 3.

Suorakulmiokolmiossa hypotenuse määritetään Pythagoras -lauseella. Näillä arvoilla se on √10, niin että:

Sec (α) = hypotenuse / vierekkäinen cateto = √10 / 1 = √10.

Samoin β = Arcot (4) vastaa sitä, että pinnasänky (β) = 4.

Suorakulmion suorakulmiokolmio, joka on 4 yksikön β ja 1 yksikön vastakkainen kateto, rakennetaan siten, että pinnasänky (β) = 4/1.

Kolmio saadaan heti päätökseen etsimään hypotenusia Pythagorasin lauseen ansiosta. Tässä tapauksessa siinä osoittautui √17 -yksiköt. Sitten CSC (β) = hypotenuse / vastakkainen cateto = √17 / 1 = √17 lasketaan.

Se voi palvella sinua: y = 3Sen (4x) toimintojakso

Muistamme, että lauseke, joka meidän on laskettava, on: 

SEC (Arcan (3)) + CSC (Arcot (4)) = Sec (α) + CSC (β) =…

… = √10 + √17 = 3,16 + 4,12 = 7,28.

- Harjoitus 2

Löydä ratkaisut:

Cos (2x) = 1 - sen (x)

Ratkaisu

On välttämätöntä, että kaikki trigonometriset toiminnot ilmaistaan ​​samassa argumentissa tai kulmassa. Käytämme kaksoiskulman identiteettiä:

Cos (2x) = 1 - 2 Sen²(x)

Sitten alkuperäinen lauseke pelkistetään:

1 - 2 Sen²(x) = 1 - sin x

Kun se on yksinkertaistettu ja ottanut huomioon, se ilmaistaan ​​seuraavasti:

sin (x) (2 sen (x) - 1) = 0

Joka antaa kaksi mahdollista yhtälöä: sin (x) = 0 liuoksella x = 0 ja toinen yhtälö Sen (x) = ½ x = π/6 liuoksena.

Ratkaisut nostettuun yhtälöön ovat: x = 0 tai x = π/6.

- Harjoitus 3

Etsi seuraavan trigonometrisen yhtälön ratkaisut:

cos (x) = synti²(x)

Ratkaisu

Tämän yhtälön ratkaisemiseksi on kätevää sijoittaa yhden tyyppinen trigonometrinen funktio, joten käytämme perustavanlaatuista trigonometristä identiteettiä siten, että alkuperäinen yhtälö kirjoitetaan seuraavasti:

cos (x) = 1 - cos²(x)

Jos nimeämme y = cos (x), lauseke voidaan kirjoittaa uudelleen:

ja² + ja - 1 = 0

Se on toisen asteen yhtälö ja jonka ratkaisut ovat:

y = (-1 ± √5) / 2

Sitten alkuperäisen yhtälön täyttävien x: n arvot ovat:

x = arcos ((-1 ± √5) / 2)

Todellinen ratkaisu on positiivinen merkki x = 0,9046 rad = 51,83º.

Toinen ratkaisu on kompleksi: x = (π - 1,06 i) rad.

Viitteet

1. Hazewinkel, M. 1994. Matematiikan tietosanakirja. Kluwer Academic Publishers / Springer Science & Business Media. 
2. Matkapuhelin. Käänteiset trigonometriset toiminnot. Toipunut: Matemovil.com
3. Maailmankaikkeuden kaavat. Käänteiset trigonometriset toiminnot. Toipunut: UniversOformulat.com
4. Weisstein, Eric W. Keksitty trigonometriset toiminnot. Toipunut: MathWorld.Susi.com
5. Wikipedia. Keksitty trigonometriset toiminnot. Haettu: vuonna.Wikipedia.com