Leikkaus pyrkimykset lasketaan ja ratkaistaan ​​harjoituksia

Se tunnetaan nimellä leikkauslujuus mikä johtuu kahden voiman asettamisesta rinnakkain alueen kanssa ja vastakkaiseen suuntaan. Tällä tavoin esine voidaan jakaa kahteen osaan, jolloin osiot liukuvat toiseen.

Päivittäiset suorat leikkausrasitukset kankaille, paperille tai metalleille, jotka ovat saksilla, giljotiinilla tai leikkauksella. Ne esiintyvät myös rakenteissa, kuten pultit tai ruuvit, nastat, palkit, kiilat ja hitsat.

Kuvio 1. Saksilla tehdään leikkauspyrkimys. Lähde: Pixabay

On tarpeen selventää, että sitä ei aina ole tarkoitettu leikkaamaan tai leikkaamaan, mutta leikkauspyrkimys taipumus muodostaa vääryyden kohde, johon sitä käytetään; Siksi leikkauspyrkimyksille kohdistuvilla palkeilla on taipumus yhdistää oman painonsa. Seuraavat esimerkit selventävät pisteen.

Kuvio 2 esittää yksinkertaisen järjestelmän, joka kuvaa yllä olevaa. Se on esine, jolla kaksi voimaa toimii vastakkaisiin suuntiin. Siellä on kuvitteellinen leikkuutaso (sitä ei ole piirretty) ja voimat vaikuttavat tason molemmille puolille, leikkaamalla kahdessa palkissa.

Saksien tapauksessa: Jokainen arkki tai reuna soveltaa voimaa leikataan objektin risti (pyöreälle) osaan, erottaen sen yhtä hyvin kahteen osaan, kuten kuvan 1 merkkijono.

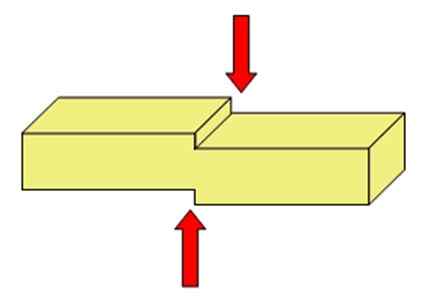Kuva 2. Kaksi osoitettua joukkoa pyrkii yleensä erottamaan palkin kahteen. Lähde: Adre-es [CC BY-SA 4.0 (https: // creativecommons.Org/lisenssit/by-SA/4.0)] [TOC]

Leikkauspyrkimys voi aiheuttaa muodonmuutoksia

Voit yrittää harjoittaa leikkausponnistelua liu'uttamalla kättäsi suljetun kirjan kansille. Toisen kannen on pysyttävä kiinnitettynä taulukkoon, joka voidaan saavuttaa tukemalla vapaata kättä niin, että se ei liiku. Kirja muodostuu hiukan tällä toiminnolla, kuten seuraavassa kuvassa on suunniteltu:

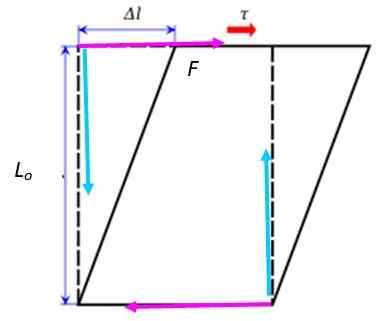Kuva 3. Kun levitetään leikkauspyrkimys kirjaan, on muodonmuutos. Lähde: Krishnavedala [CC0]

Jos tätä tilannetta analysoidaan huolellisesti, joihin kaksi jo mainittiin, mutta tällä kertaa sovellettiin vaakasuoraan (Fuksissa-A. Yksi on hänen kätensä toisella kasvolla ja toinen levitetään kiinnitetyn kirjan vastakkaisella pinnalla.

Voi palvella sinua: hitaus

Kirja ei käänny, vaikka nämä voimat voivat aiheuttaa vääntömomentin tai nettomomentin. Tämän välttämiseksi ovat kaksi muuta pystysuoraa voimaa (turkoosi); Se, jota levittiin toisella kädellä ja taulukon normaalilla, jonka nettomomentti toimii vastakkaiseen suuntaan estäen kiertoliikkeen.

[TOC]

Kuinka leikkauspyrkimys lasketaan?

Leikkaustoimenpiteet ilmestyvät jopa ihmiskehon sisällä, koska veri, kun pyöreä on jatkuvasti tangentiaalisia voimia verisuonten sisäpinta, aiheuttaen pieniä muodonmuutoksia seinissä.

Sen huomio on tärkeä epäonnistumisen epäonnistumisen mahdollisuuksien määrittämiseksi. Leikkaamalla ponnisteluja voiman lisäksi otetaan huomioon myös alue, jolla se toimii.

Tämä ymmärretään heti, kun otetaan kaksi samanpituista lieriömäistä palkkia, jotka on tehty samalla materiaalilla, mutta eri paksuudella ja alistamalla ne kasvaviin ponnisteluihin, kunnes ne rikkovat.

On selvää, että tarvittavat voimat ovat hyvin erilaisia, koska yksi palkki on ohuempi kuin toinen; Pyrkimys on kuitenkin sama.

Leikkauspyrkimys on merkitty kreikkalaisten lyrics τ (tau) ja lasketaan sovelletun voiman suuruuden välillä F ja alue -Lla pinnasta, jolla se toimii:

τ_keskiverto= F /a

Näin laskettu ponnistus tuottaa keskimääräisen voiman kyseisellä pinnalla, koska voima ei vaikuta pinnan ainutlaatuiseen kohtaan, vaan jakautuu kaikkeen siihen eikä yhtenäisellä tavalla. Jakaumaa voidaan kuitenkin edustaa tietylle pisteeseen vaikuttavalla tuloksena olevalla voimalla.

Se voi palvella sinua: Block Algebra: elementit, esimerkit, ratkaisut harjoitukset

Leikkausjännityksen mitat ovat voimaa pinnalla. Kansainvälisen järjestelmän yksiköissä vastaa Newton/Metro Square -yksikköä, yksikkö nimeltään Pascal ja lyhennetty PA.

Ne ovat samoja paineyksiköitä, joten englantilaisen järjestelmän yksiköt kuin punta -fuerza/piirakka ² ja Vaaka-fuerza /tuuma² Ne ovat myös sopivia.

Leikkaus- ja muodonmuutos

Monissa tilanteissa leikkausjännityksen suuruus on verrannollinen esineen aiheuttamaan yhtenäiseen muodonmuutokseen, kuten edellisen esimerkin kirjaan, joka palaa alkuperäisiin mittoihinsa heti, kun käsi poistetaan. Siinä tapauksessa:

Leikkauslujuus ∝ yhtenäisen muodonmuutoksen

Suhteellisuusvakio tässä tapauksessa on leikkausmoduuli, jäykkyysmoduuli tai leikkausmoduuli (g):

Leikkaus vaivaa = kuule moduulin X yksikön muodonmuutos

τ = g. γ

Γ: n kanssa = ΔL/l_jompikumpi, Missä δLens Se on ero lopullisen pituuden ja alkuperäisen välillä. Yhdistämällä annetut yhtälöt, ponnistelun aiheuttama muodonmuutoksen lauseke löytyy:

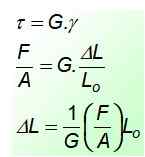
Vakion arvo G Sitä löytyy taulukoista ja sen yksiköt ovat samat kuin ponnisteluissa, kun otetaan huomioon, että yksikön muodonmuutos on mitoiton. Melkein aina G on puolet tai kolmas arvosta JA, Joustavuusmoduuli.

Itse asiassa ne liittyvät ilmaisuun:

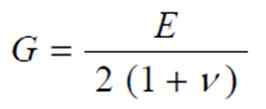
Missä ν on Poisson -moduuli, toinen materiaalin joustava vakio, jonka arvo on välillä 0 - ½. Siksi G puolestaan ​​on välillä E/3 ja E/2.

Ratkaisut

-Harjoitus 1

Kahden rautalevyn liittämiseksi käytetään teräsruuvia, joiden on kestävä leikkuut, jopa 3200 N. Mikä on ruuvin minimimahka, jos turvakerroin on 6.0 -? Tiedetään, että materiaali kestää jopa 170 x 10⁶ N/m².

Voi palvella sinua: Valkoinen kääpiö

Ratkaisu

Ruuvin altistuminen leikkaustyöt tulevat alla olevista kuvioista esitetyistä voimista. Turvakerroin on ulottumaton määrä ja liittyy maksimiin sallituihin ponnisteluihin:

Leikkauspyrkimys = f/a = suurin sallittu ponnistus/turvallisuuskerroin

Siksi alue on:

A = F X -turvakerroin / Leikkauspyrkimys = 3200 x 6/170 x 10⁶ = 0.000113 m²

Ruuvialue annetaan πd: llä²/4, siksi halkaisija on:

D -d²= 4 x a/π = 0.000144 m²

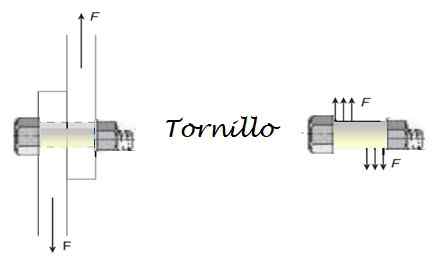Kuva 4. Ruuvin leikkaus. Lähde: Itse tehty.

D = 0.012 m = 12 mm.

-Harjoitus 2

Puulaivaa tai tacoa käytetään estämään hihnapyörän käännös jännitteistä T₁ ja T₂, 3 tuuman akselin suhteen. PIN -koodit on esitetty kuvassa. Löydä tacon leikkausjännityksen suuruus, jos esitetyt voimat toimivat hihnapyörällä:

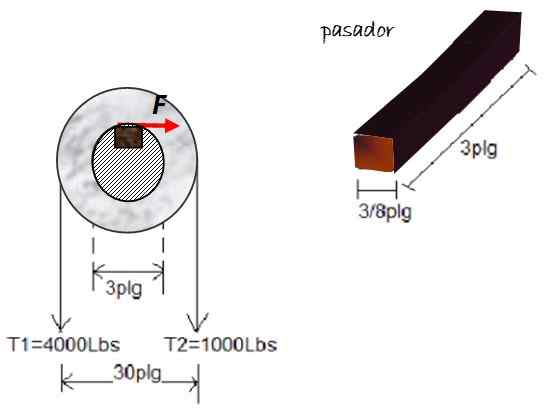Kuva 5. Esimerkiksi ilmainen kehon kaavio 2. Lähde: Itse tehty.

Ratkaisu

T₁ tuottaa vääntömomentin hihnapyörän anti -antihorarium -merkityksessä, jolle on annettu positiivinen merkki, kun taas T₂ Tuottaa vääntömomentin negatiivisella merkinnällä. 15 tuuman vipuvarsi jokaiselle jännitykselle. Siksi:

Nettomomentti = 4000 kiloa voima . 15 tuumaa - 1000 kiloa -. 15 tuumaa = 45000 kiloa . tuuma

Puisen tacon ei pitäisi kääntyä, sitten tacon keskustaan ​​liittyvien hetkien on oltava nolla. F edustaa pinnan keskimääräistä voimaa:

Neljä viisi.000 - f.D = 0

Kanssa D = 1.5 tuumaa, siksi:

F x 1.5 = 45.000

F = 30.000 kiloa

Tämä voima aiheuttaa voimakkaan suuruusponnistelun:

τ = f/a = 30.000 kiloa fuerza / (3/8 x 3) tuumaa² = 2.67 x 10⁴ Libras-fuerza/inchga²

Viitteet

1. Olut, f. 2010. Materiaalimekaniikka. Viides. Painos. McGraw Hill. 7 - 9.
2. Fitzgerald, 1996. Materiaalimekaniikka. Alfa -omega. 21-23.
3. Giancoli, D.  2006. Fysiikka: sovellusten periaatteet. 6^th  Ed. Prentice Hall. 238-242.
4. Hibbeler, R.C. 2006. Materiaalimekaniikka. Kuudes. Painos. Pearson -koulutus. 22 -25
5. Valera Negrete, J. 2005. Yleiset fysiikan muistiinpanot. Yksinäinen. 87-98.
6. Wikipedia. Leikkausrasitus. Toipunut: vuonna.Wikipedia.org.