Kaava- ja yhtälöiden jännitteen ponnistus, laskenta, harjoitukset

Hän Stressi rasitus Se on määritelty voimana kohtisuorassa aluetta kohtaan yksikköä kohden, joka on asetettu esineeseen sen päissä harjoittaakseen vetovoimaa, jonka pidentäminen pidentää. Sen mitat ovat voimaa / aluetta, ja matemaattisessa muodossa voimme ilmaista sen seuraavasti:

τ = f / a

Kansainvälisen yksikköjärjestelmän ponnistelujen yhtenäisyys on sama, jota käytetään paineeseen: Pascal, lyhennetty PA, joka vastaa 1 Newton/ M².

Kuvio 1. Jos jännityspyrkimys ylittää tietyn arvon, köysi on rikki. Lähde: Pxhere.

Jännityspyrkimyksessä on kaksi voimaa, jotka koskevat samaan suuntaan ja vastakkaisiin aisteihin, jotka venyttävät vartaloa. Jos alun perin esineen pituus oli l_jompikumpi, Jännitystyötä sovellettaessa uusi pituus on L ja ΔL -venytys lasketaan:

Δl = l - l_jompikumpi

Kiinteillä esineillä on joustavuus suuremmassa tai pienemmässä määrin, mikä tarkoittaa, että kun jännityspyrkimys katoaa, ne palaavat alkuperäisiin mittoihinsa.

Tämä tapahtuu, mikäli pyrkimys ei ole niin suuri, että ne aiheuttavat pysyvän muodonmuutoksen. Kumi-, kumi- tai kumi -materiaalit ovat hyviä joustaville esineille, ja niillä on myös tämä laatu hiukset ja iho, muun muassa.

[TOC]

Yhtenäiset muodonmuutokset

Kun tutkitaan kuinka ruumiit ovat muodonmuutos jännitteessä, on erittäin kätevää määritellä käsite Yhtenäiset muodonmuutokset, Vapautettu määrä. Yhtenäistä muodonmuutoksia merkitään kreikkalaisella kirjaimella δ (pienet "delta") ja lasketaan seuraavasti:

Δ = ΔL /l_jompikumpi

Yhtenäisen muodonmuutoksen tarkoituksena on arvioida suhteellisesti objektin muodonmuutosta jännityksessä. Katsotaanpa se tällä tavalla: Ei ole sama venyttää 1 cm 1 metrin pituinen palkki, venyttää 1 cm toiseen 10 m pitkälle. Ensimmäisessä tapauksessa muodonmuutos on paljon merkittävämpi kuin toisessa.

Se voi palvella sinua: Ohm: Resistenssimittaukset, esimerkit ja liikunta ratkaistu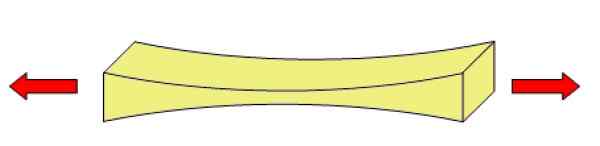Kuva 2. Jännitys- tai vetoponnisteluja käyttävä kohde on muodonmuutos. Lähde: Wikimedia Commons.

Kuinka jännityspyrkimys lasketaan? (Esimerkkejä)

Newtonin englanti ja nykyaikainen fyysikko nimeltä Robert Hooke (1635-1703), tutkivat ruumiiden elastisia ominaisuuksia ja perustivat lain, joka kantaa hänen nimensä. Sen avulla pyrkimykset sovellettiin kokeneen muodonmuutokseen, kun ponnistus on pieni, liittyy:

Ponnistus ∝ muodonmuutos (yksikkö)

On loogista olettaa, että mitä suurempi stressipyrkimys tapahtuu, suurempi pidentyminen tapahtuu. Yllä olevien määritelmien hyödyntäminen:

τ ∝ Δ

Tasa -arvon määrittämiseksi tarvittava suhteellisuusvakio merkitään ja tunnetaan nuorena moduulina tai elastisuusmoduulina, joka on ominaista materiaaleille:

τ = y⋅δ

Youngin moduulilla on samat jännitysyksiköt, koska yksikön muodonmuutos on mitoiton.

Joten tapa laskea stressipyrkimys elastisilla ominaisuuksilla varustetussa kehossa, on muodonmuutoksen mittaaminen ja sen nuoren moduulin tunteminen. Tämä määrä on määritetty kokeellisesti monille materiaaleille ja se on taulukko.

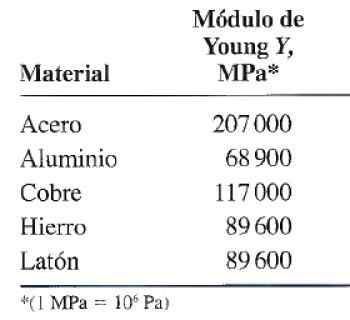Kuva 3. Youngin joustavuus tai moduulimoduulitaulukko joitain yleisiä käyttöä varten. Lähde: Valera Negrete, J. 2005. Yleiset fysiikan muistiinpanot. Yksinäinen.

Esimerkki laskennasta

Oletetaan, että halkaisijaltaan 3 mm: n karkaistu teräs altistuu jännitysponnisteluun, joka roikkuu siitä 250 N paino, mikä olisi mainitun ponnistelun suuruus?

No, voimme käyttää jännityspyrkimyksen määritelmää pintaan kohtisuoran voiman ja mainitun pinnan alueen välillä. Lasketaan ensin alue olettaen, että pyöreä ristikkäinen johdin:

Se voi palvella sinua: Massumero: Mikä se on ja miten se saa (esimerkkien kanssa)

A = π . (D/2)² =  π . (D² /4)

Langan halkaisija on 3 mm ja nämä yksiköt on muutettava metreiksi:

D = 3 x 10^-3 m.

A = π . (3 x 10^-3 m)² / 4 = 7.07 x 10^-6 m².

Jännityspyrkimykset saadaan langasta roikkuvalla painolla, jota käytetään kohtisuoraan sen poikkileikkaukselle, siksi:

τ = 250 N / 7.07 x 10^-6 m² = 3.5 x 10 ⁷ Paa

Pascal on melko pieni yksikkö, joten kertoimet eivät ole epätavallisia. Tietäen, että 1 mega-pascal (MPA) on 10⁶ Pascal, jännityspyrkimys on edelleen:

τ = 35 MPa

Ratkaisut

- Harjoitus 1

Sauvan joustavuusmoduuli on 4 x 10^yksitoista Paa. Mikä yksikön muodonmuutos saadaan soveltamalla 420 MPa?

Ratkaisu

Käytettävä yhtälö on:

τ = y⋅δ

Sen kanssa laskemme yhtenäisen muodonmuutoksen:

Δ = τ / y = 420 x 10⁶ PA/ 4 x 10^yksitoista PA = 0.00105

Δ = ΔL /l_jompikumpi

Siksi muodonmuutos ΔL on:

ΔL = 0.00105 l_jompikumpi

Jos esimerkiksi sauva oli alun perin 1 metri pitkä, sillä jännityksellä se venyttää vain 0.00105 m = 1.05 mm.

- Harjoitus 2

Teräslanka on 1.50 m pitkä ja halkaisija 0.400 mm. Yksi päistä on kiinnitetty katolle ja toiseen asetetaan massaheijastin m = 1.50 kg, joka vapautetaan. Laskea:

a) lanka venymä.

b) Yhtenäisen muodonmuutoksen ja yhtenäisen muodonmuutoksen prosenttiosuus. Onko mahdollista, että heijastimen paino rikkoo lankaa?

Ratkaisu

Lanka ulottuu, koska heijastin altistuu jännitysponnisteluihin. Tämän ponnistelun tuottama voima on heijastimen paino.

Se voi palvella sinua: fysiikkaa ennen kreikkalaisia ​​(Antigua Kreikka)

Massaobjektin paino on massan tuote painovoiman kiihtyvyyden arvolla, siksi:

F = 1.50 kg x 9.8 m/s² = 14.7 n

Langan osion ristikkäin tarvitaan:

A =  π . (D² /4) = π x (0.4 x 10-3 m) 2/4 = 1.26 x 10^-7 m².

Näiden tulosten avulla johdossa tehdyt ponnistelut lasketaan:

τ = 14.7 N / 1.26 x 10^-7 m² = 1.17 x 10⁸ Paa

Langalla on joustava käyttäytyminen, joten on pätevä olettaa, että Hooken laki täytetään:

τ = y⋅δ

Joustavuusmoduulitaulukosta havaitaan, että teräkselle y = 207 x 10⁹ Paa. Lisäksi yhtenäinen muodonmuutos on:

Δ = ΔL /l_jompikumpi

Korvaaminen yhtälössä ponnisteluille:

τ = y⋅δ = y⋅ (ΔL /l_jompikumpi-A

Siksi venytys on:

ΔL = l_jompikumpi τ / y =

= 1.50 m x 1.17 x 10⁸ PA / 207 x 10⁹ PA = 8.5 x 10^-4 M = 0.849 mm.

Langan yhtenäinen muodonmuutos on:

Δ = ΔL /l_jompikumpi = 8.5 x 10^-4 m / 1.5 m = 5.652 x 10^-4

Jos ilmaisemme sen prosentteina, yhtenäisen muodonmuutoksen prosenttiosuus on 0.0565 %, alle 0.1 %, siksi odotetaan, että lanka vastustaa heijastimen painoa rikkomatta, koska sen kokemat muodonmuutokset eivät ole liian suuria verrattuna alkuperäiseen pituuteen.

Viitteet

1. Bauer, W. 2011. Fysiikka tekniikkaan ja tieteisiin. Osa 1. MC Graw Hill.
2. Olut, f. 2010. Materiaalimekaniikka. McGraw Hill. Viides. Painos.
3. Giancoli, D.  2006. Fysiikka: sovellusten periaatteet. Kuudes. Ed Prentice Hall.
4. Sears, Zemansky. 2016. Yliopiston fysiikka, jolla on moderni fysiikka. 14. päivä. Ed. Osa 1.
5. Valera Negrete, J. 2005. Yleiset fysiikan muistiinpanot. Yksinäinen.