Pohja- ja mittavektoritila, aksioomit, ominaisuudet

Eräs vektoriatila Se on ei -tyhjäsarja V= tai, v, W -,…, joiden elementit ovat vektoreita. Niiden kanssa suoritetaan joitain tärkeitä operaatioita, joista seuraavat erottuvat:

- Summa kahden vektorin välillä U + V tuloksena z -z, joka kuuluu koko V.

- Real -luvun α kertominen vektorilla v- α v Se antaa toisen vektorin ja joka kuuluu V.

Taiteellinen visio vektoritilasta. Lähde: Pixabay

Merkitsemällä vektoria, jota käytämme rohkeaa (v Se on vektori), ja skalaareille tai numeroille kreikkalaiset kirjaimet (α on numero).

[TOC]

Aksioomit ja ominaisuudet

Vektorialueena olisivat seuraavat kahdeksan aksioomaa täytettävä:

1 käynti: tai +v = v +tai

2-transitiivisuus: (tai + v-A + W - = tai + ( v + W --A

NULL-vektorin 3-olemassaolo 0 - sellainen 0 - + v = v

4-olemassa olevaa: päinvastaista: päinvastoin v On (-v-A , olettaen että v + (-v) = 0 -

5 tuotejakavuus vektorisumman suhteen: α ( tai + v ) = αtai +αv

6 tuotejakavuus skalaarisumman suhteen: (α + β)v = αv +βv

Skalaarituotteen 7-assosiaatio: α (β v) = (α β)v

8-numero 1 Se on neutraali elementti, koska: 1v = v

Esimerkkejä vektoritiloista

Esimerkki 1

Tason (R²) vektorit ovat esimerkki vektoritilasta. Tasossa oleva vektori on geometrinen esine, jolla on suuruus ja suunta. Sitä edustaa suuntautunut segmentti, joka kuuluu mainitulle tasolle ja jonka koko on verrannollinen sen suuruuteen.

Kahden tason vektorin summa voidaan määritellä toisen vektorin geometriseksi toiminnaksi ensimmäisen jälkeen. Summan tulos on suuntautunut segmentti, joka alkaa ensimmäisen alkuperästä ja saavuttaa toisen kärjen.

Kuvassa voidaan huomata, että R²: n summa on kommutatiivinen.

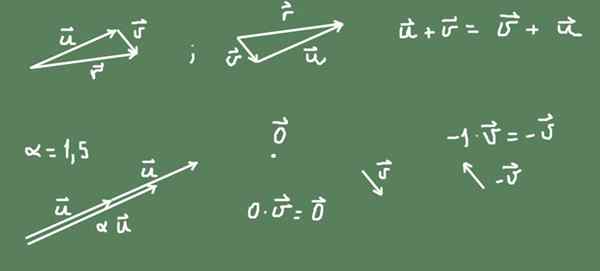Kuva 2. Vektorit tason muotovektoritilassa. Lähde: Itse tehty.

Α -numeron tuote määritellään myös vektorilla. Jos numero on positiivinen, alkuperäinen vektoriosoite ylläpidetään ja koko on α -kertainen alkuperäinen vektori. Jos numero on negatiivinen, osoite on päinvastainen ja tuloksena oleva vektorikoko on numeron absoluuttinen arvo.

Vektori vastustaa vektoria v On -v = (-1) v.

NULL -vektori on piste R² -tasossa, ja vektorin nolla -numero johtaa nollavektoriin.

Kaikki sanottu on esitetty kuvassa 2.

Esimerkki 2

Aseta P Kaikista polynomeista, jotka ovat pienempi tai yhtä suuret kuin kaksi, mukaan lukien nollaluokka, ne muodostavat sarjan, joka täyttää kaikki vektoritilan aksioomit.

Se voi palvella sinua: toisiaan poissulkevat tapahtumat: ominaisuudet ja esimerkit

Olla polynomi p (x) = a x² + b x + c y q (x) = d x² + e x + f

Kahden polynomin summa on määritelty: p (x) + q (x) = (a + d) x² + (b + e) ​​x + (c + f)

Koko kuuluvien polynomien summa P Se on kommutatiivinen ja transitiivinen.

Koko NULL POLYNOMIAALI P Se on kaikki sen kertoimet yhtä suuri kuin nolla:

0 (x) = 0 x² + 0 x + 0

A -skalaarin summa määritetään polynomilla, kuten: α p (x) = α ∙ A x² + α ∙ B x + α ∙ C

P (x): n vastakkainen polynomi on -p (x) = (-1) p (x).

Kaikista edellä mainituista seuraa, että sarja P Kaikista polynomeista, jotka ovat vähemmän tai yhtä suuret kuin kaksi, se on vektoritila.

Esimerkki 3

Aseta M Kaikista M -rivien x n -sarakkeista, joiden elementit ovat todellisia lukuja, muodostavat todellisen vektoritilan suhteessa matriisin matriisien summaan ja tuoteeseen matriisi.

Esimerkki 4

Todellisen muuttujan jatkuvien funktioiden sarja F muodostaa vektoritilan, koska kahden funktion summa voidaan määritellä, skalaarin kertolasku funktiolla, nollafunktiolla ja symmetrisella funktiolla. Ne täyttävät myös vektoritilaa kuvaavat aksioomit.

Vektoritilan pohja ja ulottuvuus

Pohja

Sarja lineaarisesti riippumattomia vektoreita määritellään vektoritilan perustaksi siten, että lineaarisesta yhdistelmästä niiden vektoritilan vektori voidaan luoda.

Kahden tai useamman vektorin lineaarisesti yhdistäminen koostuu vektorien kertomisesta jollain skalaarilla ja sitten lisäämällä ne vektorisesti.

Esimerkiksi vektoritilassa kolmen ulottuvuuden muodossa, jonka muodostuu r³: n määrittelemä kanoninen emäs (suuruus 1) (suuruusluokkaa 1) (suuruus 1) Yllyttää, J -, k -k -.

Missä Yllyttää = (1, 0, 0); J - = (0, 1, 0); k -k - = (0, 0, 1). Nämä ovat Cartesian tai kanonisia vektoreita.

Mikä tahansa vektori V R³ kuuluminen on kirjoitettu V = a Yllyttää + b - J - + c k -k -, joka on perusvektoreiden lineaarinen yhdistelmä Yllyttää, J -, k -k -. Skalaarit tai numerot A, B, C tunnetaan kartesian komponentteina V.

Sanotaan myös, että vektoritilan perusvektorit muodostavat joukon vektoritilaa.

Ulottuvuus

Vektoritilan ulottuvuus on vektoripohjan kardinaali määrä mainitulle tilalle; eli mainitun pohjan muodostavien vektorien lukumäärä.

Tämä kardinaali on kyseisen vektoritilan lineaarisesti riippumattomien vektorien enimmäismäärä, ja samalla vähimmäismäärä vektoreita, jotka muodostavat generoivan sarjan mainittua tilaa.

Voi palvella sinua: Tilastollinen väestö: käsite, tyypit, esimerkit

Vektoritilan emäkset eivät ole ainutlaatuisia, mutta kaikilla saman vektoritilan emäksillä on sama ulottuvuus.

Vektori -alatila

Vektoritilan V vektori -alatila on V -osajoukko, jossa samat toiminnot määritetään kuin V ja täyttää kaikki vektoritilan aksioomit. Siksi alatila on myös vektoritila.

Esimerkki vektori -alatilasta ovat vektorit, jotka kuuluvat XY -tasoon. Tämä alatila on alaryhmä, jonka ulottuvuus on suurempi kuin kolmen dimensionaaliseen tilaan kuuluva vektorisarja XYZ.

Toinen esimerkki vektorialueen vektoritilasta S1 muodostuu kaikilla 2 × 2 -matriiseilla, joilla on oikeat elementit, alla on määritelty:

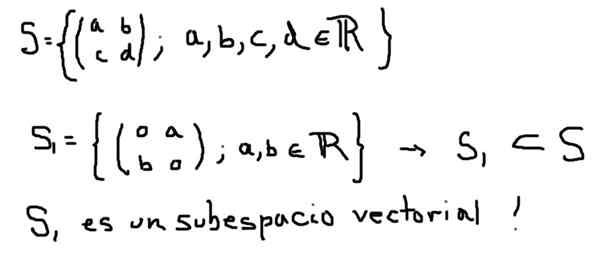
Toisaalta S2 on määritelty alla, vaikka se on S -osajoukko, se ei muodosta vektorialatikaa:

Ratkaisut

-Harjoitus 1

Olla vektoria V1= (1, 1, 0); V2= (0, 2, 1) ja V3= (0, 0, 3) R³: ssä.

a) Todista, että he ovat lineaarisesti riippumattomia.

b) Todista, että ne muodostavat pohjan R³: ssä, koska mikä tahansa luettelo (x, y, z) voidaan kirjoittaa lineaarisena yhdistelmänä V1, V2, V3.

c) Löydä luettelon komponentit V = (-3,5,4) pohjassa V1, V2, V3.

Ratkaisu

Kriteeri lineaarisen riippumattomuuden osoittamiseksi on luoda seuraavat yhtälöjoukot a, β: ssa ja y: ssä

α (1, 1, 0) + β (0, 2, 1) + γ (0, 0, 3) = (0, 0, 0)

Siinä tapauksessa, että ainoa ratkaisu tähän järjestelmään on α = β = γ = 0, niin vektorit ovat lineaarisesti riippumattomia, muuten ne eivät ole.

A -arvojen, β: n ja y: n arvojen saavuttamiseksi ehdotamme seuraavaa yhtälöjärjestelmää:

α ∙ 1 + β ∙ 0 + γ ∙ 0 = 0

α ∙ 1 + β ∙ 2 + γ ∙ 0 = 0

α ∙ 0 + β ∙ 1 + γ ∙ 3 = 0

Ensimmäinen johtaa a = 0, toinen α = -2 ∙ β, mutta kuten α = 0, sitten β = 0. Kolmas yhtälö tarkoittaa, että γ = (-1/3) β, mutta kuten β = 0 sitten γ = 0.

Vastaa

Päätelee, että se on joukko lineaarisesti riippumattomia vektoreita R³: ssä .

Vastaus b

Kirjoitetaan nyt luettelo (x, y, z) v1, v2, v3 lineaarisena yhdistelmänä.

(x, y, z) = α V1 + β V2 + γ V3 = α (1, 1, 0) + β (0, 2, 1) + γ (0, 0, 3)

α ∙ 1 + β ∙ 0 + γ ∙ 0 = x

α ∙ 1 + β ∙ 2 + γ ∙ 0 = y

Se voi palvella sinua: Tukey -testi: Mikä on esimerkiksi ratkaistu harjoitus

α ∙ 0 + β ∙ 1 + γ ∙ 3 = z

Missä sinulla on:

α = x

α + 2 β = y

β + 3 γ = z

Ensimmäinen osoittaa α = x, toinen β = (y-x)/2 ja kolmas γ = (z-y/2 +x/2)/3. Tällä tavoin olemme löytäneet minkä tahansa R³ -luettelon a-, β: n ja y -generaattorit 

Vastaus C

Löydämme luettelon komponentit V = (-3,5,4) pohjassa V1, V2, V3.

Korvaamme vastaavat arvot yllä olevien lausekkeissa generaattoreille.

Tässä tapauksessa meillä on: α = -3; β = (5-(-3))/2 = 4; γ = (4-5/2 +(- 3)/2)/3 = 0

Tuo on:

(-3,5,4) = -3 (1, 1, 0) + 4 (0, 2, 1) + 0 (0, 0, 3)

Lopuksi:

V = -3 V1 + 4 V2 + 0 - V3

Päätämme sen V1, v2, v3 Ne muodostavat pohjan ulottuvuuden 3 vektoritilaan r³.

-Harjoitus 2

Express polynomi P (t) = T² + 4T -3 P1 (t) = T² -2T + 5, P2 (T) = 2T² -3T ja P3 (T) = T + 3.

Ratkaisu

P (t) = x p1 (t) + ja p2 (t) + z p3 (t)

missä numerot x, y, z on määritettävä.

Kertomalla ja ryhmittelemällä termejä samalla asteella t: ssä, se saadaan:

T² + 4 t -3 = (x + 2y) t² + (-2x -3y + z) t + (5x + 3z)

Mikä johtaa meidät seuraavaan yhtälöjärjestelmään:

x + 2y = 1

-2x -3y + z = 4

5x + 3z = -3

Tämän yhtälöjärjestelmän ratkaisut ovat:

x = -3, y = 2, z = 4.

Tuo on:

P (t) = -3 p1 (t) + 2 p2 (t) + 4 p3 (t)

-Harjoitus 3

Näytä vektorit V1= (1, 0, -1, 2); V2= (1, 1, 0, 1) ja V3= (2, 1, -1, 1) R⁴: stä ovat lineaarisesti riippumattomia.

Ratkaisu

Yhdistämme lineaarisesti kolme vektoria V1, V2, V3 Ja vaadimme yhdistelmää lisäävät r⁴: n nolla -elementin

-lla V1 + b - V2 + c V3 = 0 -

Tarkoittaen,

A (1, 0, -1, 2) + B (1, 1, 0, 1) + C (2, 1, -1, 1) = (0, 0, 0, 0)

Tämä johtaa meidät seuraavaan yhtälöjärjestelmään:

A + B + 2 C = 0

B + C = 0

-A - C = 0

2 a + b + c = 0

Vähennä ensimmäinen ja neljäs meillä on: -a + c = 0 mikä merkitsee a = c.

Mutta jos tarkastelemme kolmatta yhtälöä, meidän on = -c. Ainoa tapa tavata a = c = (-c) on, että C on 0 ja siksi tulee myös 0.

A = c = 0

Jos korvaamme tämän tuloksen ensimmäisessä yhtälössä, päättelemme, että b = 0.

Lopuksi a = b = c = 0, joten voidaan päätellä, että vektorit V1, V2 ja V3 ovat lineaarisesti riippumattomia.

Viitteet

1. Lipschutz, S. 1993. Lineaarialgebra. Toinen painos. McGraw - Hill. 167 - 198.