Onko Scallene -kolmioita suorassa kulmassa?

Scalele -kolmioita on suorassa kulmassa. Ennen aiheen etenemistä on ensin tarpeen tuntea olemassa olevat erityyppiset kolmiot. Kolmiot luokitellaan kahdella luokalla, jotka ovat: niiden sisäkulmat ja niiden sivujen pituudet.

Minkä tahansa kolmion sisäkulmien summa on aina yhtä suuri kuin 180º. Mutta sisäisten kulmien mukaan toimenpiteet luokitellaan seuraavasti:

-Akuttaa: Nämä kolmiot ovat sellaisia, että niiden kolme kulmaa ovat akuutteja, ts. Ne mittaavat alle 90 °.

-Suorakulmio: Ne ovat niitä kolmioita, joilla on suorakulma, ts. Kulma, joka mittaa 90 °, ja siksi kaksi muuta kulmaa ovat akuutteja.

-Tylppä: Ne ovat kolmioita, joilla on räikeä kulma, ts. Kulma, jonka mitta on suurempi kuin 90 °.

Scalan -kolmiot, joissa on suorakulma

Kiinnostuksena tässä osassa on selvittää, voivatko skaleenikolmiossa olla oikea kulma.

Kuten edellä sanotaan, suorakulma on kulma, jonka mitta on 90º. On tarpeen tietää vain skaleenikolmion määritelmä, joka riippuu kolmion sivujen pituudesta.

Kolmioiden luokittelu heidän puolensa mukaan

Heidän sivujensa pituuden mukaan kolmiot luokitellaan seuraavasti:

-Tasasivuinen: Ne ovat kaikki nämä kolmiot siten, että heidän kolmen sivunsa pituudet ovat samat.

-Sammutus: Ne ovat kolmiot, joilla on tarkalleen kaksi yhtä pitkää puolta.

-Skaaleeni: Ne ovat kolmioita, joilla kolmella puolella on erilaiset toimenpiteet.

Vastaavan kysymyksen muotoilu

Otsikon vastaava kysymys on ”Onko siellä kolmioita, joilla on kaikki kolme puolta eri toimenpiteillä, ja tämän kulma on 90 °?"

Alussa todettu vastaus on kyllä. Tätä vastausta ei ole kovin vaikea perustella.

Jos huolellisesti havaitaan, mikään suorakaiteen kolmio ei ole tasapainossa, tämä voidaan perustella suorakulmiokolmioiden Pythagoras -lauseen ansiosta:

Kun otetaan huomioon suorakulmion kolmio, jonka mukaan niiden luokkien pituudet ovat "A" ja "B", ja sen hypotenuksen pituus on "C", sinun on c² = a²+b², mikä voidaan nähdä, että hypoteenin pituus " C "on aina suurempi kuin kunkin jalan pituus.

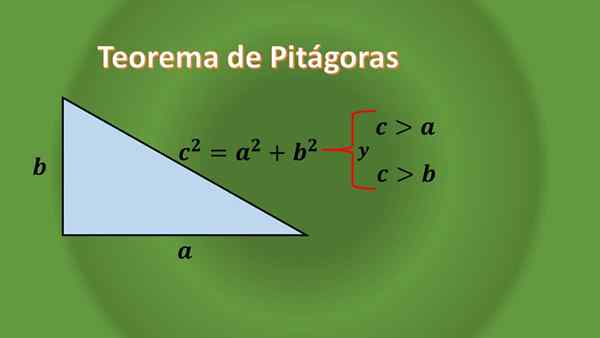
Kuten "A" ja "B" ei sanota mitään, tämä tarkoittaa, että oikea kolmio voidaan olla samoitus- tai scallene.

Valitse sitten vain kaikki suorakulmiokolmiot siten, että sen jaloilla on erilaiset toimenpiteet, ja siten Scaleen -kolmio, jolla on suorakulma, on valittu.

Esimerkit

-Jos tarkastellaan suorakaiteen kolmiota, joiden jalkojen pituudet ovat vastaavasti 3 ja 4, niin Pythagoras -lauseen avulla voidaan päätellä, että hypotenusen pituus on 5. Tämä tarkoittaa, että kolmio on Scalene ja siinä on suorakulma.

-Olkoon ABC suorakulmiokolmio mittausten mittauksilla 1 ja 2. Sitten sen hypoteenin pituus on √5, joka päättelee, että ABC on Scaleenin suorakulmio kolmio.

Jokaisessa mittakaavan kolmiossa ei ole suorakulmaa. Voit harkita seuraavan kuvan kaltaista kolmiota, joka on Scalene, mutta mikään sen sisäkulmista ei ole suora.

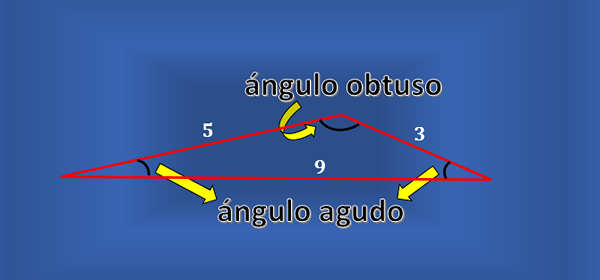Lisäksi jokainen oikea kolmio ei ole Scalene. Jos harkitset oikeaa kolmiota, jonka jalat mittaavat molemmat 1, hypotenusen mitta on √2. Siksi suorakulmio kolmio on samanaikainen.