Yleiset tekijäominaisuudet, esimerkit, harjoitukset

Hän yhteinen tekijä algebrallinen lauseke on määrä, jota on läsnä kaikessa. Kun yleinen tekijä tiedetään, on mahdollista kirjoittaa lauseke vastaavalla tavalla tekijöiden tuotteen läpi.

Kaikilla algebrallisilla lausekkeilla ei ole yleistä tekijä. Esimerkki ilmaisusta, jolla ei ole yleistä tekijää, on:

x + y

Kuvio 1. Algebrallisen ekspression yleinen tekijä tekee siitä kahden tekijän osoitetun tuotteen. Lähde: Pixabay.

Sen sijaan tämä kyllä:

5a + 10b

On nähdään, että 5 on läsnä molemmissa termeissä, koska 10 = 5 ∙ 2. Koska 5 on yleinen tekijä, seuraava voidaan kirjoittaa:

5a + 10b = 5 ∙ (a + 2b)

Lukija voi tarkistaa jakautuvan ominaisuuden läpi, että oikealla oleva lauseke on yhtä suuri kuin alkuperäinen.

Yleinen tekijä voi olla myös kirjaimellinen tai lukujen ja kirjaimien yhdistelmä, esimerkiksi 4x² - 2x. Se x ja 2 Ne ovat tekijöiden ja lausekkeen välillä pysyy tuotteena:

4x² -2x = 2x⋅ (x -1)

Etuna löydettäessä ilmaisun yhteinen tekijä ja sen kirjoittaminen tuotteena on, että sen kanssa on melkein aina helppo käyttää. Siksi sitä käytetään monissa algebrallisissa ja laskentamenetelmissä, kuten:

-Ratkaiseessa yhtälöitä, joiden ratkaisut paljastetaan nopeasti, kun yleinen tekijä löytyy.

-Laskettaessa rajaa määrittelemättömyydellä, tämä voi kadota asianmukaisesti ottamalla huomioon.

-Asianmukainen tekijä helpottaa myös operaatioita rationaalisilla algebrallisilla lausekkeilla, kuten summilla ja vähennyksillä.

[TOC]

Yleiset tekijäominaisuudet

Yleisen tekijän pääominaisuudet ovat seuraavat:

-Se voi olla numero, algebrallinen ekspressio tai molempien yhdistelmä.

-Yleinen tekijä on sisällytettävä jokaisessa ekspression termissä tekijä.

Voi palvella sinua: Transsendenttiset toiminnot: Tyypit, määritelmä, ominaisuudet, esimerkit

-Sen sisältämien ehtojen määrän mukaan voi olla:

1. Yleinen monomitekijä, jos yhteinen tekijä on yhden termin,
2. Yleinen binomitekijä, jos sinulla on kaksi termiä ja
3. Yleinen polynomitekijä, jos yleinen tekijä koostuu useista termeistä.

Kuinka löytää algebrallisen ekspression yhteinen tekijä?

Polynomista läsnä olevan yhteisen tekijän löytämiseksi sinun on laskettava kaikkien termien numeeristen kertoimien maksimaalinen yhteinen jakaja tai MCD, samoin kuin kunkin termin kirjaimet tai kirjaimet ja valitse voima pienimmästä eksponentista.

Kirjeet tai kirjaimet voidaan esitellä monomiaaleina, binomeina tai polynomeina, kuten seuraavissa esimerkeissä nähdään.

Suositeltavin yleisen tekijän hankkimisprosessin ymmärtämiseksi on seurata esimerkkejä ja harjoittelua useiden harjoitusten ratkaiseminen kussakin tapauksessa.

Yhteiset tekijäesimerkit

Emme saa unohtaa sitä tosiasiaa, että yhteisen tekijän tavoite muunnetaan lauseke osoitetuksi tekijöiden tuotteiksi. Silloin merkittävimmät tapaukset analysoidaan:

Yleinen monomakerroin

Sinulla on seuraavat monomiaalit (yksittäiset algebralliset lausekkeet):

2x²; 10x⁴ja; 100x⁶ja²

Mikä voi olla yhteinen tekijä kolmelle?

Alkaen numeerisista kertoimista: 2, 10 ja 100, kaikki ovat tasaisia ​​ja niiden MCD on 2. Kirjaimellisen osan suhteen muuttuja X on läsnä kolmessa termissä, ja alhaisin teho on x², Sitten yhteinen tekijä on 2x².

Kolme ehdotettua termiä voidaan kirjoittaa tämän tekijän tuotteina tällä tavalla:

2x²= 2x²∙ 1

10x⁴y = 2x² ∙ 5x²ja

100x⁶ja²= 2x²∙ 50x⁴ja²

Kertomalla oikealla olevat tekijät, voidaan varmistaa, että vasemman termi saadaan.

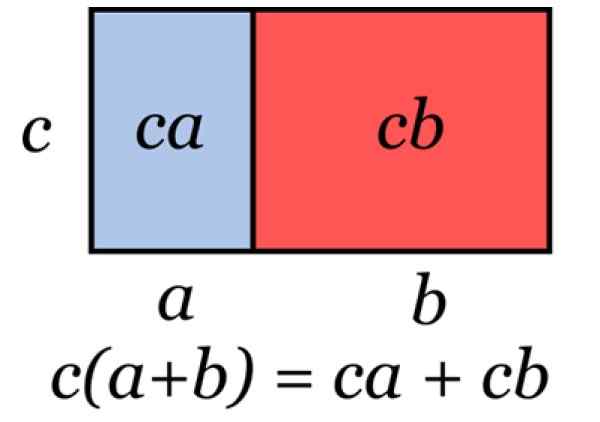Kuva 2. Kuva, joka edustaa yleistä tekijää. Lähde: Wikimedia Commons.

Tätä tekniikkaa sovelletaan, kun sitä tarvitaan algebrallisen ekspression ottamiseksi, kuten seuraavissa esimerkeissä:

• Esimerkki 1

Tosiasia seuraava ilmaisu:

Se voi palvella sinua: Iskosceles -kolmio

5x³ja + 10x²ja² + 5xy²

Kunkin termin numeeristen kertoimien MCD on:

MCD (5.10) = 5

Mitä kirjaimelliseen osaan, molemmat x kuin ja Niitä on läsnä kolmessa termissä ja kunkin vähiten eksponentti on 1, joten yhteinen tekijä on 5xy Ja voit kirjoittaa:

5x³ja + 10x²ja² + 5xy²= 5xy ∙ (x² +2xy²+ja)

Yleinen polynomitekijä

Yleinen tekijä voi koostua binomiaalista, trinomista tai yleensä polynomissa. Tässä tapauksessa edellisen osan ohjeet ovat edelleen voimassa, valitaan yleisenä tekijänä, jolla on pienin eksponentti.

• Esimerkki 2

Kirjoita seuraava lauseke kahden tekijän tuote:

2a (x - 1) - 3b (x -1)

Suoran tarkastuksen perusteella yhteinen tekijä on binomiaalinen (X-1), niin:

2a (x - 1) - 3b (x - 1) = (x -1) ∙ (2a - 3b)

Tekijä ryhmittelemällä termejä

Joskus yhteisen tekijän olemassaolo ei ole ilmeinen, mutta paljastetaan, jos termit on ryhmitelty kätevällä tavalla:

• Esimerkki 3

Foektoida 3x³ - 9AX² - x + 3a

Ensi silmäyksellä ei ole yhteistä tekijää näillä neljällä termeillä, koska esimerkiksi x Se on läsnä kolmessa ensimmäisessä, mutta ei viimeisessä. Ja -lla Se on toisessa ja viimeisessä.

Kertoimien osalta on kolme termiä, joilla 3 on läsnä, mutta se on kuitenkin yleinen tekijä, sen pitäisi olla kaikilla termeillä.

Näyttää siltä, ​​että kuvattuja tekniikoita ei voida soveltaa tällä kertaa. Ilmaisu voi kuitenkin olla factoring ryhmittelemällä kaksi ensimmäistä termiä ja kaksi viimeistä, ja ne ovat varovaisia ​​asettaessaan suluja, että merkit ovat tarkoituksenmukaisia ​​olemaan muuttamatta alkuperäistä:

Voi palvella sinua: vektorin suorakulmaiset komponentit (harjoituksilla)

3x³ - 9AX² - x + 3a = (3x³ - 9AX²) - (x - 3a)

Huomaa negatiivinen merkki sulujen keskellä: se on välttämätöntä, koska muuten alkuperäinen lauseke muuttuu.

Vasemmassa sulkuissa yleinen tekijä on 3x², siksi:

(3x³ - 9AX²) - (x - 3a) = 3x²⋅ (x - 3a) - (x - 3a)

Ja havaitaan, että yleinen tekijä on jo ilmestynyt: (x - 3a), Toisin sanoen toisen kerran on tekijä:

3x² (x- 3a) - (x - 3a) = (x - 3a) ∙ ( 3x²- 1)

Yhteiset tekijäharjoitukset

Harjoitus 1

Ratkaise 4x -yhtälö³ +7x²  +6x = 0

Ratkaisu

"X" on yleinen tekijä, siksi:

3x³ −5x²  +2x = x (3x² −5x +2) = 0

Vasemmalla oleva lauseke on 0, riittää, että yksi näistä kahdesta olosuhteesta täyttyy:

x = 0

JOMPIKUMPI:

3x² −5x +2 = 0

Tämä on täydellinen toisen asteen yhtälö, joka voidaan ratkaista soveltamalla yleistä kaavaa, myös käyttämällä tieteellistä laskinta tai muuta algebrallista menetelmää. Tämän yhtälön ratkaisut ovat:

x = 1

x = 2/3

Kun löydetään, on havainnollistava kirjoittaa yhtälö 3 tekijän tuote, vaikka lausunnossa ei ollut sitä pyytänyt sitä. Se olisi näin:

x⋅ (x-1) ⋅ (x-2/3) = 0

Harjoitus 2

Laske seuraava raja, jos se on olemassa:

Ratkaisu

Ensin se korvataan x = −2: lla yrittää arvioida rajaa, niin se saadaan:

Koska se on 0/0 -muodon määrittelemätöntä, sinun on oltava tekijä yrittää poistaa se. Nimittäjä ei voi olla tekijä, mutta osoittaja tekee.

Laskennassa yleinen tekijä on x-

x²+2x = x ∙ (x+2)

Faktoroidun ekspression korvataan rajalla ja tällä tavoin määrittelemättömyys katoaa:

Johtopäätöksenä on, että raja on olemassa ja on arvoinen −2.

Viitteet

1. Baldor, a. 2005. Algebra. Kulttuuriryhmä.
2. Jiménez, r. 2008. Algebra. Prentice Hall.
3. Larson, r. 2012. Ennakkoluulo. Kahdeksas. Painos. Cengage -oppiminen.
4. Stewart, J. 2007. Precculment: Laskentamatematiikka. Viides. Painos. Cengage -oppiminen.
5. Zill, D. 1984. Algebra ja trigonometria. McGraw Hill.