Yleinen tekijä termien ryhmittelyssä, harjoitukset

Hän yleinen tekijä termien ryhmittelyssä Se on algebrallinen menettely, joka mahdollistaa joidenkin algebrallisten lausekkeiden kirjoittamisen tekijöiden muodossa. Tämän tavoitteen saavuttamiseksi ilmaisun on ensin oltava kätevästi ryhmittelyä ja tarkkailua, että jokaisella siten muodostetulla ryhmällä on käytännössä yhteinen tekijä.

Tekniikan soveltaminen oikein vaatii jonkin verran harjoittelua, mutta lyhyessä ajassa on mahdollista hallita. Katsotaanpa ensin havainnollistava esimerkki askel askeleelta. Sitten lukija voi soveltaa mitä he oppivat jokaisessa harjoituksessa, jotka ilmestyvät sen jälkeen.

Kuvio 1. Poista yleinen tekijä ryhmittelytermeissä helpottaa algebrallisten lausekkeiden kanssa. Lähde: Pixabay.

Oletetaan esimerkiksi, että sinun on otettava huomioon seuraava lauseke:

2x² + 2xy - 3zx - 3zy

Tämä algebrallinen ekspressio koostuu neljästä monomialista tai termistä, jotka on erotettu merkkeillä + ja -, nimittäin:

2x², 2xy, -3zx, -3zy

Tarkkailemalla huolellisesti, X on yhteinen kolmen ensimmäiselle, mutta ei viimeiseen, kun taas ja on yhteinen toiselle ja neljännelle, ja Z on yhteinen kolmannelle ja neljännelle.

Joten periaatteessa ei ole yhteistä tekijää samanaikaisesti neljälle termille, mutta jos ne on ryhmitelty, kuten se näytetään seuraavassa osassa, yksi voi auttaa kirjoittamaan lauseke kahden tai useamman tekijän tuotteena.

[TOC]

Esimerkit

Tekijä ekspressio: 2x² + 2xy - 3zx - 3zy

Vaihe 1- Ryhmä

2x² + 2xy - 3zx - 3zy = (2x² + 2xy) + (-3zx - 3zy)

Vaihe 2: Poista yleinen tekijä jokaisesta ryhmästä

2x² + 2xy - 3zx - 3zy =

= (2x² + 2xy) - (3zx + 3zy) =

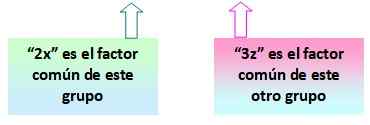
= 2x (x+y) - 3z (x+y)

YllyttääMerkitys: Negatiivinen merkki on myös yleinen tekijä, joka on otettava huomioon.

Voi palvella sinua: vektoritila: pohja ja mitta, aksioomit, ominaisuudet

Huomaa nyt, että sulku (x+y) toistetaan kahdella termeillä, jotka on saatu ryhmittyessä. Se on yleinen tekijä, joka etsii.

Vaihe 3: Vaikuta kaikki lauseke

2x² + 2xy - 3zx - 3zy = (x+y) (2x - 3z)

Edellisessä tuloksessa tekijän tavoite on saavutettu, mikä ei ole kukaan muu kuin muuntaa algebrallinen ekspressio, joka perustuu summiin ja termien vähentämiseen, kahden tai useamman tekijän, esimerkissamme,: (x+ y) tuotteessa: (x+ y) ja (2x - 3z).

Tärkeitä kysymyksiä yhteisestä ryhmäkertoimesta

Kysymys 1: Kuinka tietää, että tulos on oikea?

Vastaus: Jakautuva ominaisuus sovelletaan saatuun tulokseen, ja siten saavutetun lausekkeen vähentämisen ja yksinkertaistamisen jälkeen on oltava samanaikaisesti alkuperäisen, ellei ei, virhe on virhe.

Edellisessä esimerkissä se toimii käänteisesti tuloksen kanssa varmistaakseen, että se on hieno:

(x+y) (2x - 3z) = 2x² -3zx +2xy - 3zy

Koska lisäysjärjestys ei muuta summaa, jakautumisominaisuuden soveltamisen jälkeen kaikki alkuperäiset termit ovat mukana merkkejä, joten tekijä on oikea.

Kysymys 2: Voisitko ryhmitellä toisella tavalla?

Vastaus: On algebrallisia ilmaisuja, jotka myöntävät useamman kuin yhden ryhmittelymuodon ja muut, jotka eivät. Valitussa esimerkissä lukija voi kokeilla muita mahdollisuuksia, esimerkiksi ryhmittely:

2x² + 2xy - 3zx - 3zy = (2x²- 3zx) + (2xy - 3zy)

Ja voit nähdä, että tulos on sama kuin täällä saatu. Optimaalisen ryhmän löytäminen on käytännössä.

Voi palvella sinua: Kohdosta johdettu: Laskenta, esittely, harjoitukset

Kysymys 3: Miksi on välttämätöntä saada yleinen tekijä algebrallisesta ekspressiosta?

Vastaus: Koska on sovelluksia, joissa faktoroidut ekspressiot helpottavat laskelmia. Oletetaan esimerkiksi, että haluat tehdä 2x² + 2xy - 3zx - 3zy yhtä suuri kuin 0. Mikä olisi mahdollisuudet?

Tätä huolenaiheen vastaamista, faktoroitu versio on paljon hyödyllisempi kuin alkuperäinen kehitys. Se syntyy näin:

(x+y) (2x - 3z) = 0

Yksi mahdollisuus, että lauseke on arvon arvoinen, on, että x = -y, z: n arvosta riippumatta. Ja toinen on, että x = (3/2) z, ilman y -arvoa.

Harjoitukset

- Harjoitus 1

Hanki seuraavan ilmaisun yleinen tekijä ryhmittelemällä termejä:

AX+AY+BX+BY

Ratkaisu

Kaksi ensimmäistä on ryhmitelty, yhteisen tekijän "A" ja kahdella viimeisellä tekijällä "B":

AX+AY+BX+by = a (x+y)+b (x+y)

Kun tämä on tehty, paljastetaan uusi yleinen tekijä, joka on (x+y), niin että:

AX+AY+BX+by = a (x+y)+b (x+y) = (x+y) (a+b)

Toinen tapa ryhmitellä

Tämä ilmaus myöntää toisen tavan ryhmittely. Katsotaanpa, mitä tapahtuu, jos termit järjestetään uudelleen ja ryhmä on tehty, jolla ne sisältävät X: n ja toisen niiden kanssa, jotka sisältävät ja:

AX +AY +BX +BY = AX +BX +AY +BY = X (A +B) +Y (A +B)

Tällä tavoin uusi yleinen tekijä on (A+B):

AX+AY+BX+BY = AX+BX+AY+BY = X (A+B)+Y (A+B) = (X+Y) (A+B)

Tämä johtaa samaan tulokseen ryhmittelytavan ensimmäisestä tapauksesta, jonka se testattiin.

- Harjoitus 2

Seuraava algebrallinen lauseke on kirjoitettava kahtena tekijätuotteena:

Kolmas³ - Kolmas²B+9AB²--lla²+AB-3B²

Voi palvella sinua: Coplanares -pisteet: Yhtälö, esimerkki ja ratkaisut harjoitukset

Ratkaisu

Tämä lauseke sisältää 6 termiä. Yritetään ryhmitellä ensimmäinen ja neljäs, toinen ja kolmas ja lopulta viides ja kuudes:

Kolmas³ - Kolmas²B+9AB²--lla²+AB-3B² = (3³ --lla²) + (- 3²B+9AB²) + (AB-3B²-A

Nyt jokainen sulku on tekijä:

= (3³ --lla²) + (- 3²B+9AB²) + (Ab -3b²) = a² (3a -1) + 3ab (3b -a) + b (a -3b)

Ensi silmäyksellä näyttää siltä, ​​että tilanne on ollut monimutkainen, mutta lukijaa ei pidä lannistaa, koska aiomme kirjoittaa viimeisen kauden uudelleen:

-lla² (3a -1) + 3ab (3b -a) + b (a -3b) = a² (3a - 1) + 3ab (3b -a) - b (3b -a)

Kahdella viimeisellä termillä on nyt yhteinen tekijä, joka on (3B-A), joten ne voidaan ottaa huomioon. On erittäin tärkeää olla unohtaa ensimmäisen termin² (3a - 1), jonka on jatkettava kaiken mukana lisäämistä, joten et työskentele hänen kanssaan:

-lla² (3a - 1) + 3ab (3b -a) - b (3b -a) = a² (3a-1) + (3b-a) (3ab-b)

Expression on pelkistetty kahteen termiin ja viimeisimmässä löydetään uusi yhteinen tekijä, joka on "B". Nyt se on:

-lla² (3a-1) + (3b-a) (3ab-b) = a² (3a-1) +b (3b-a) (3a-1)

Seuraava yleinen tekijä esiintymisessä on 3. - 1:

-lla² (3a - 1) +b (3b -a) (3a -1) = (3a - 1) [a² + B (3B-A)]

Tai jos haluat ilman neliömäisiä sidekkeitä:

(3. - 1) [a² + B (3b -a)] = (3a - 1) (a² -AB + 3B²-A

Voiko lukija löytää toisen ryhmittelytavan, joka johtaa samaan tulokseen?

Kuva 2. Ehdotetut tekijäharjoitukset. Lähde: f. Zapata.

Viitteet

1. Baldor, a. 1974. Perusalgebra. Venezuelan kulttuurinen s.-Lla.
2. Jiménez, r. 2008. Algebra. Prentice Hall.
3. Tärkeimmät tekijät. Toipunut: Julioprofe.netto.
4. Yksinäinen. Matematiikka: tekijä ryhmittelemällä termejä. Kirjanpidon ja hallinnon tiedekunta.
5. Zill, D. 1984. Algebra ja trigonometria. MacGraw Hill.