Tilavuusvirta

Selitämme, mikä tilavuusvirta on, miten se lasketaan ja siihen vaikuttavat tekijät

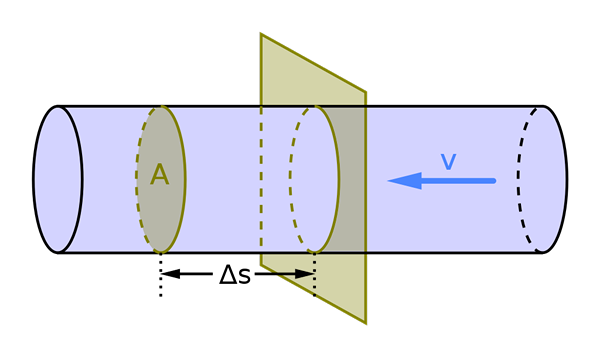
Tilavuusvirta riippuu poikkileikkauksen A pinta -alasta ja nesteen nopeudesta V. Lähde: Mikerun, CC BY-SA 4.0, Wikimedia Commons

Mikä on tilavuusvirta?

Hän tilavuusvirta Se mahdollistaa nesteen määrän määrittämisen, joka ylittää kanavan osan ja tarjoaa nopeusmittauksen, jolla neste liikkuu samalla. Siksi sen toimenpide on erityisen mielenkiintoinen muun muassa teollisuuden, lääketieteen, rakentamisen ja tutkimuksen alueilla.

Nesteen nopeuden mittaaminen (joko neste, kaasu tai molempien seos) ei kuitenkaan ole niin yksinkertaista kuin kiinteän rungon siirtymänopeus voi olla mittaus. Siksi tapahtuu, että nesteen nopeuden tuntemiseksi on tarpeen tietää sen virtaus.

Tästä ja monista muista nesteistä liittyvät kysymykset, nesteen mekaniikan tarjoamat fysiikan haara. Virtaus määritellään kuinka nestettä kanavan osa on läpi, se on jo putkilinja, putkilinja, joki, kanava, verenkierto jne., Väliaikaisen yksikön huomioon ottaminen.

Yleensä lasketaan tilavuus, jonka tietty alue aikayksikössä, jota kutsutaan myös tilavuusvirtaukseksi. Myös massa- tai massavirta, joka ylittää tietyn ajankohtana määritetyn alueen, vaikka sitä käytetään harvemmin kuin tilavuusvirtaus.

Kuinka tilavuusvirta lasketaan?

Volumetrinen virtaus edustaa kirjaimella Q. Tapauksissa, joissa virtaus siirtyy kohtisuoraan kuljettajan osaan nähden, se määritetään seuraavalla kaavalla:

Q = a = v / t

Tässä kaavassa A on kuljettajan osio (se on keskimääräinen nopeus, joka nesteellä on), v on tilavuus ja t aika. Koska kansainvälisessä järjestelmässä kuljettajan alue tai osa mitataan M: ssä² Ja nopeus m/s, virtaus mitataan m³/s.

Voi palvella sinua: 21 Tärkeää fysiikan tapahtumaa

Tapauksissa, joissa nesteen siirtymän nopeus luo kulman θ, jonka suunnassa kohtisuorassa on pintaosaa A, virtauksen määrittäminen on seuraava:

Q = cos θ

Tämä on yhdenmukainen edellisen yhtälön kanssa, koska kun virtaus on kohtisuorassa pinta -alaan A, θ = 0 ja siksi, cos θ = 1.

Yllä olevat yhtälöt ovat totta vain, jos nesteen nopeus on tasainen ja jos osan osa on tasainen. Muutoin tilavuusvirta lasketaan seuraavan integraalin kautta:

Q = ∫∫_s V D S

Tässä kiinteässä ds on pintavektori, joka määritetään seuraavalla lausekkeella:

Ds = n ds

Siellä n on normaali yksikkövektori kanavan pintaan ja ds differentiaalipintaelementti.

Jatkuvuusyhtälö

Puristamattomien nesteiden ominaisuus on, että nesteen massa säilytetään kahdella osalla. Siksi jatkuvuusyhtälö täyttyy, joka luo seuraavan suhteen:

ρ₁ -Lla₁ V₁ = ρ₂ -Lla₂ V₂

Tässä yhtälössä ρ on nesteen tiheys.

Pysyvän virtauksen järjestelmätapauksissa, joissa tiheys on vakio, ja siksi on täyttynyt, että ρ₁ = ρ₂, Se on pelkistetty seuraavaan lausekkeeseen:

-Lla₁ V₁ = A₂ V₂

Tämä vastaa vakuuttamista, että virtaus säilyy ja siksi:

Q -₁ = Q₂.

Edellä esitetyn havainnosta seuraa, että nesteet kiihtyvät, kun ne saavuttavat kapeamman osan kanavasta, samalla kun ne vähentävät nopeuttaan, kun ne saavuttavat laajemman osan kanavasta. Tällä tosiasialla on mielenkiintoisia käytännön sovelluksia, koska se sallii leikkiä nesteen siirtymisen nopeudella.

Voi palvella sinua: Subatomiset hiukkaset

Bernoulli -periaate

Bernoulli -periaate määrittää, että ihanteelliselle nesteelle (ts. Neste, jolla ei ole viskositeettia tai kitkaa), joka liikkuu kiertojärjestelmässä suljetun kanavan kautta, täyttyy, että sen energia pysyy vakiona koko sen siirtymänsä ajan.

Viime kädessä Bernoulli -periaate ei ole muuta kuin nesteen virtauksen energiansuojelulain muotoilu. Siten Bernoulli -yhtälö voidaan muotoilla seuraavasti:

H +V² / 2g+p/ ρg = vakio

Tässä yhtälössä H on korkeus ja G on painovoiman kiihtyvyys.

Bernoulli -yhtälössä nesteen energia otetaan huomioon milloin tahansa, energia, joka koostuu kolmesta komponentista.

• Kineettinen komponentti, joka sisältää energiaa, johtuen nopeudesta, jolla neste liikkuu.
• Gravitaatiopotentiaalin tuottama komponentti nesteen sijaitsevan korkeuden seurauksena.
• Virtausenergian komponentti, joka on nesteen energiaa paineesta johtuen.

Tässä tapauksessa Bernoulli -yhtälö ilmaistaan ​​seuraavasti:

H ρ g +(v² ρ)/2 + p = vakio

Loogisesti, todellisen nesteen tapauksessa Bernoulli -yhtälön ilmaisua ei täytetä, koska nesteen siirtymisessä kitkahäviöt ja on välttämätöntä keskittää monimutkaisempi yhtälö.

Mikä vaikuttaa tilavuusvirtaukseen?

Volumetrinen virtaus vaikuttaa, jos kanava on tukkeutunut.

Voi palvella sinua: kevyt taittuminen: elementit, lait ja kokeilu

Lisäksi tilavuusvirta voi muuttua myös lämpötilan ja paineenmuutoslämpötilan vaikutuksesta ja paineesta, johon se on.

Yksinkertainen menetelmä tilavuusvirtauksen mittaamiseksi

Todella yksinkertainen menetelmä tilavuusvirtauksen mittaamiseksi on antaa nestevirtaus mittaussäiliössä tietyn ajanjakson ajan.

Tämä menetelmä ei yleensä ole kovin käytännöllinen, mutta totuus on, että on erittäin yksinkertainen ja erittäin havainnollistava ymmärtää nesteen virtauksen merkitys ja merkitys.

Tällä tavoin nesteen annetaan virtata mittaussäiliöön tietyn ajanjakson ajan, kertynyt tilavuus mitataan ja tulos saatu ajan välinen ajan jaetaan.

Viitteet

1. Virtaus (neste) (n.d -d.-A.  Wikipediassa. ES: stä palautettu.Wikipedia.org.
2. Tilavuusvirtaus (n.d -d.-A.  Wikipediassa. Haettu jstk.Wikipedia.org.
3. Engineers Edge, LLC. "Nesteen tilavuuden virtausnopeusyhtälö". Reuna -insinöörit
4. Mott, Robert (1996). "1". Käytetty nestemekaniikka (4. painos). Meksiko: Pearson Education.
5. Batchelor, g.K -k -. (1967). Johdatus nestedynamiikkaan. Cambridge University Press.
6. Landau, L.D -d.; Lifshitz, E.M. (1987). Fluidimekaniikka. Teoreettisen fysiikan kurssi (2. ed.-A. Pergamon Press.