Dynaaminen tai kineettinen kitkakerroin, esimerkit, harjoitukset

Se Dynaaminen kitka tai kineettinen Se tapahtuu kahden kosketuksessa olevien kahden kappaleen välillä, kun yhden niistä pinta liikkuu suhteessa toisen pintaan. Esimerkiksi laatikossa, joka liu'uttaa kitkaa kaltevuuteen.

Kaltevuuden on oltava riittävän suuri, joten painon tangentiaalinen komponentti on yhtä suuri tai voittaa kitkavoiman, muuten laskeutuva lohko päättyy pysähtymään.

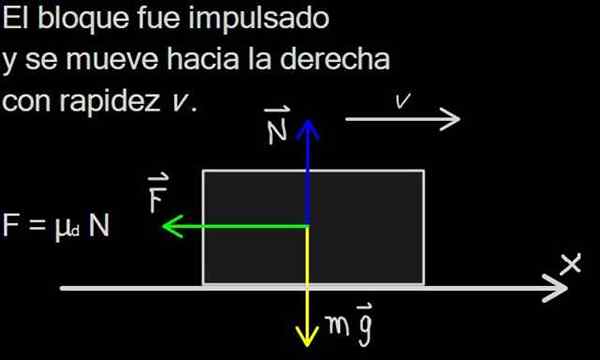
Kuvio 1. Kitkavoima jakautuu lohkon kosketuspinnalle, mutta voimakaaviossa se on esitetty yhtenä voimana F, lähteenä: F. Zapata

Kitkajoukolla on erittäin tärkeä merkitys jokapäiväisessä elämässä, koska se sallii ihmisten, eläinten ja ajoneuvojen liikkumisen. Kitkattomalla pinnalla, kuten jäätelöllä, ei ole mahdollista aloittaa liikettä.

Kitka antaa myös autojemme pysähtyä, kun ne liikkuvat.

Jarruja levitettäessä jarrutyynyjä kiristetään pyörälevyjä vastaan ​​ja dynaamisen kitkan ansiosta lopeta niiden kierto. Mutta ei riitä, että sinulla on hyviä jarruja, on välttämätöntä, että renkaiden ja lattian välillä on riittävästi kitkavoimaa, koska lopulta tämä on voima, josta olemme riippuvaisia ​​niin, että auto pysähtyy.

Ihmiskunta on oppinut käsittelemään kitkaa sen eduksi. Siten alkoi kitka kahden kuivapuun välissä tulen valmistukseen.

Luonto on myös oppinut käsittelemään kitkaa sen puolesta. Esimerkiksi nivelten luita peittävät nivelkalvot ovat yksi pinnoista, joilla on alhaisin kitkakerroin, joka on olemassa.

[TOC]

Dynaaminen kitkakerroin

Ensimmäinen, joka tutkii systemaattisesti tasaisella pinnalla liukuvan lohkon liikettä, oli Leonardo da Vinci, mutta hänen opintonsa jäivät huomaamatta.

Voi palvella sinua: Dirac Jordan Atomic -malli: Ominaisuudet ja postulaatit

Vasta seitsemännentoista vuosisadan aikana ranskalainen fyysikko Guillaume Amontons löysi uudelleen kitkalait:

Dynaaminen kitkalaki

1.- Kitkavoima, joka on läsnä lohkossa, joka liukuu tasaiselle pinnalle, vastustaa aina liikkeen suuntaa.

2.- Dynaamisen kitkavoiman suuruus on verrannollinen lohkon pintojen ja tukitason välillä.

3.- Suhteellinen vakio on kitkakerroin, staattinen μ_ja Jos ei ole liukastumista ja dynaamista μ: tä_{d -d} Kun on. Kitkakerroin riippuu kosketuksessa olevien pintojen materiaaleista ja karheuden tilasta.

4.- Kitkajoukko on riippumaton ilmeisestä kosketusalueesta.

5.- Kun yhden pinnan liike alkaa suhteessa toiseen, kitkavoima on vakio eikä riipu pintojen suhteellisesta nopeudesta.

Tapauksessa sovelletaan liukuvaa, staattista kitkaa, jonka voima on pienempi tai yhtä suuri kuin staattinen kitkakerroin kerrottuna normaalilla.

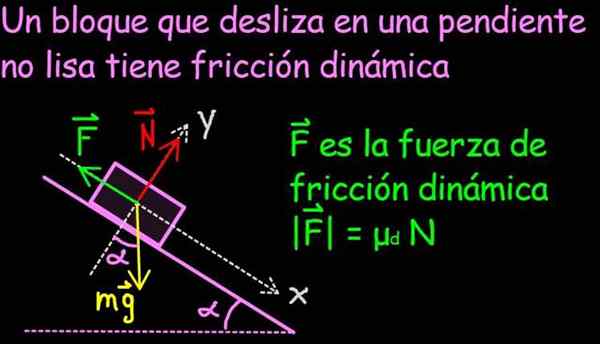
Kuva 2. Dynaaminen kitkavoima vastustaa liikkumisen suuntaa ja sen suuruutta on verrannollinen normaalin voiman suuntaan. Suhteellisuusvakio on dynaaminen kitkakerroin. Lähde: f. Zapata.

Viimeinen kiinteistö oli seurausta Ranskan fyysikon Charles Augustin of Coulombin panoksesta, joka tunnetaan paremmin kuuluisasta voimalaista tiettyjen sähköisten maksujen välillä.

Nämä havainnot johtavat meidät dynaamisen kitkavoiman matemaattiseen malliin F-

F = μ_{d -d} N

Missä μ_{d -d} Se on dynaaminen kitkakerroin ja N on normaali voima.

Kuinka määrittää dynaaminen kitkakerroin?

Kahden pinnan välinen dynaaminen kitkakerroin määritetään kokeellisesti. Sen arvo ei riipu vain molemmilla pinnoilla olevista materiaaleista, vaan myös niiden karheuden tai kiillotuksen tilasta, samoin kuin sen puhtaus.

Voi palvella sinua: mekaaniset aallot: ominaisuudet, ominaisuudet, kaavat, tyypit

Yksi tapa määrittää se on lisätä ja liu'uttaa tunnettu laatikko vaakasuoraan pinnalle.

Jos nopeus tiedetään ajettaessa ja tuosta ajasta kulkeva etäisyys mitataan, on mahdollista tuntea jarrukitkan takia jarrukiina.

Koe 

Tässä kokeessa alkuperäinen nopeus mitataan v ja etäisyys d -d, Joten jarrukiihtyvyys on:

A = - v² / 2d

Voiman kaavio on esitetty kuvassa 2. Painon suuruus on lohkon massa m, joka kerrotaan painovoiman G kiihtyvyydellä, ja kuten tiedetään, paino osoittaa aina pystysuoraan alaspäin.

N Se on normaali voima, joka johtuu tukipinnasta ja on aina kohtisuorassa (tai normaalissa) tasossa. Normaali on olemassa, kun pinnat ovat kosketuksissa ja lakkaa heti, kun pinnat on erotettu.

Voima F edustaa dynaamista kitkavoimaa. Se on todella jakautunut lohkon alapintaan, mutta voimme edustaa sitä yhtenä voimana F sovellettu lohkon keskelle.

Koska pystysuuntainen tasapaino on normaalin suuruus N Se on yhtä suuri kuin painon MG:

N = mg

Vaakasuunnassa kitkajoukko tuottaa massalohkon M hidastumisen Newtonin toisen lain mukaan:

-F = m a

Kitkavoima F osoittaa vasemmalle, joten sen vaakasuora komponentti on negatiivinen, m on lohkon massa ja A on jarrukiihdytys.

Oli aiemmin saanut A = - v² / 2d Ja myös dynaaminen kitkamalli osoittaa, että:

F = μD N

Korvaaminen edellisessä yhtälössä:

-μ_{d -d} N = - v² / 2d

Kun otetaan huomioon, että n = mg, voit jo tyhjentää dynaamisen kitkakertoimen: 

Voi palvella sinua: Schrödinger Atomic -malli

μ_{d -d} = v² / (2d mg)

Joidenkin materiaalien rocy -kerroinpöytä

Seuraava taulukko näyttää staattiset ja dynaamiset kitkakertoimet eri materiaaleille. On huomattava, että systemaattisesti staattinen kitkakerroin on aina suurempi kuin dynaaminen kitkakerroin.

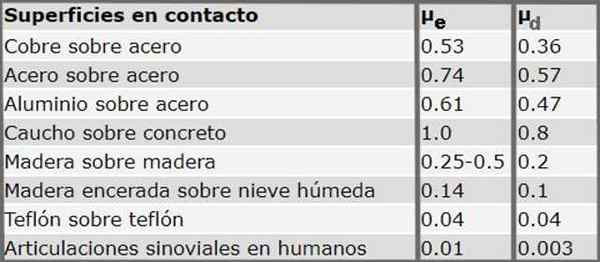Kuva 3. Staattiset ja dynaamiset kitkakertoimet useille kosketuksessa oleville pinnoille. Lähde: Serway R.-Lla. Fyysinen. McGraw-Hill (1992)

Harjoitukset

- Harjoitus 1

2 kg: n taikina vaakapohjassa mainostetaan ja se vapautetaan. Vapautumishetkellä kirjataan 1,5 m/s. Siitä hetkestä lähtien, kunnes lohko pysähtyy dynaamisella kitkalla 3 m. Määritä kineettinen kitkakerroin.

Ratkaisu

Edellisen osan esimerkissä saadun kaavan mukaan se on dynaaminen (tai kineettinen) kerroin:

μ_{d -d} = v² / (2d mg) = 1,52 / (2x3x2 x9,8) = 0,019.

- Harjoitus 2

Tietäen, että kuvan 1 lohko laskeutuu vakiona nopeudella, että lohkon massa on 1 kg ja että tason kallistus on 30º, määrittää:

a) dynaamisen kitkan arvo

b) Lohkon ja tason välinen dynaaminen kitkakerroin.

Ratkaisu

Kuviossa 4 liikeyhtälö (Newtonin toinen laki) esitetään lohkon ongelmalle, joka laskeutuu kaltevuuden kitkakertoimella μ_{d -d}  ja α -kallistus (katso kuvion 1 voimat -kaavio)

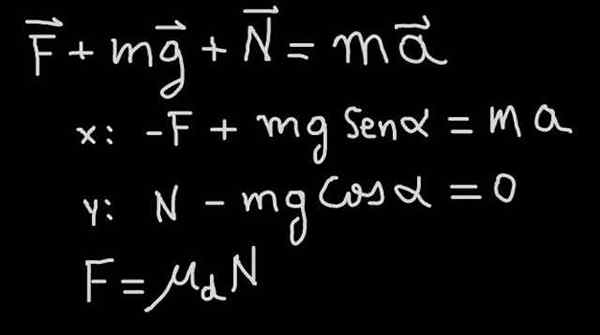Kuva 4. Newtonin toinen laki sovellettiin lohkoon, joka liukuu kitkalla. Lähde: f. Zapata.

Harjoituksessamme meille kerrotaan, että lohko laskeutuu jatkuvalla nopeudella, siksi laskeutuu kiihtyvyydellä A = 0. Sieltä seuraa, että kitkavoima on sellainen, että se on yhtä suuri kuin painon tangentiaalinen komponentti: f = mg sen (α).

Tapauksessamme M = 1 kg ja α = 30º, joten kitkavoiman F arvo on 4,9n.

Toisaalta normaali voima n on sama ja vastoin painon kohtisuoraa komponenttia: n = mg cos (α) = 8,48n .

Sieltä seuraa, että dynaaminen kitkakerroin on:

μ_{d -d} = F / n = 4,9N / 8,48N = 0,57

Viitteet

1. Alonso m., Suomalainen. 1970. Fyysinen. Osa. Mekaniikka. Inter -American Educational Fund S.-Lla.
2. Bauer, W. 2011. Fysiikka tekniikkaan ja tieteisiin. Osa 1. MC Graw Hill.
3. Hewitt, s. 2012. Käsitteellinen fysiikka. Viides painos.
4. Rex, a. 2011. Fysiikan perusteet. Pearson. 
5. Serway R. 1992. Fyysinen. McGraw-Hill.
6. Nuori, h. 2015. Yliopiston fysiikka, jolla on moderni fysiikka. 14. ed. Pearson.