Kitkatyypit, kerroin, laskenta, harjoitukset

Se kitka Se on vastus yhden pinnan siirtymiselle ollessaan kosketuksessa toisen kanssa. Se on pinnallinen ilmiö, joka tapahtuu kiinteän, nesteen ja kaasumaisen materiaalin välillä. Tangentiaalinen vastusvoima kahdelle kosketuksessa olevalle pinnalle, joka vastustaa näiden pintojen välisen suhteellisen siirtymän suuntaa, kutsutaan myös kitkavoimaan tai kitkavoimaan F_{r -}.

Kiinteän rungon syrjäyttämiseksi pinnalle on asetettava ulkoinen voima, joka voi voittaa kitkan. Kun vartalo liikkuu, kitkavoima vaikuttaa kehoon vähentäen sen nopeutta ja voi jopa pysäyttää sen.

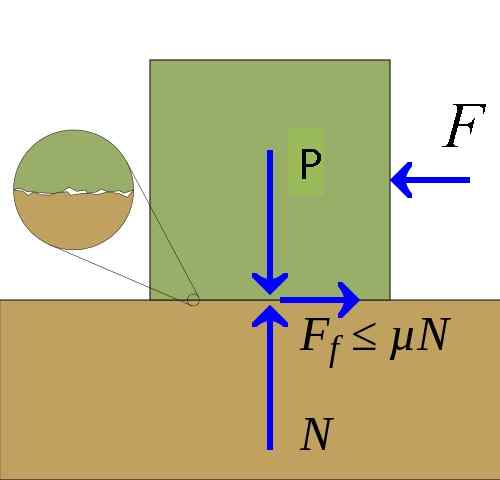
Kitka [kirjoittanut Keta, Pietter Kuiper (https: // commons.Wikimedia.org/wiki/tiedosto: kitka.Svg)]

Kitkavoima voidaan esittää graafisesti kehon voimakaavion avulla, joka on kosketuksessa pinnan kanssa. Tässä kaaviossa kitkajoukko F_{r -} Sitä piirtää tangentiaaliseen runkoon kohdistetun voiman komponentti pintaan.

Kosketuspinta käyttää reaktiovoimaa kehossa, jota kutsutaan normaaliksi voimaksi N. Joissakin tapauksissa normaali voima johtuu vain painosta P pinnalla lepäävästä kehosta ja muissa tapauksissa se johtuu muusta kuin painovoimasta kohdistuvista voimista.

Kitka on peräisin, koska kosketuksessa on mikroskooppisia rugoja. Kun yrität siirtää yhden pinnan toisella. Energiahäviöitä puolestaan ​​tuotetaan lämmön muodossa, jota ei käytetä kehon siirtämiseen.

[TOC]

Kitkatyypit

Kitkaa on kahta päätyyppiä: kitka Coulomb o Kuiva kitka ja neste kitka.

-Coulomb -kitka

Kitka Coulomb Se vastustaa aina kehon liikettä ja jaetaan kahden tyyppiseen kitkatyyppiin: staattinen kitka ja kineettinen (tai dynaaminen) kitka.

Staattisessa kitkassa pinnalla ei ole kehon liikettä. Sovellettu voima on erittäin alhainen eikä riitä kitkavoiman voittamiseen. Kitkalla on maksimiarvo, joka on verrannollinen normaaliin voimaan ja jota kutsutaan staattisiksi kitkavoimaan F_keksin.

Staattinen kitkavoima määritellään enimmäisvoimaan, joka kestää kehon liikkeen alussa. Kun sovellettu voima ylittää staattisen kitkavoiman, se pysyy sen maksimiarvossa.

Kineettinen kitka toimii, kun vartalo on liikkeessä. Kehon pitämiseen tarvittava voima kutsutaan kineettiseksi kitkavoimaan F_RC.

Kineettinen kitkavoima on pienempi tai yhtä suuri kuin staattinen kitkavoima, koska kun vartalo alkaa liikkua, on helpompaa jatkaa sen liikkumista kuin yrittää tehdä niin levossa.

Coulomb -kitkalaki

1. Kitkavoima on suoraan verrannollinen normaaliin voimaan kosketuspinnalle. Suhteellisuusvakio on kitkakerroin μ Se on kosketuksessa olevien pintojen välillä.
2. Kitkavoima on riippumaton pintojen välisen näennäisen kosketusalueen koosta.
3. Kineettinen kitkavoima on riippumaton kehon liukunopeudesta.

-Neste kitka

Kitka tapahtuu myös, kun rungot liikkuvat kosketuksessa nestemäisten tai kaasumaisten materiaalien kanssa. Tämän tyyppistä kitkaa kutsutaan neste kitkaksi, ja se määritellään vastustuskykyksi nesteen kanssa kosketuksissa olevien runkojen liikkeelle.

Se voi palvella sinua: helppoja fysiikan kokeita (ensisijainen yliopisto)

Nesteen kitka viittaa myös nesteen vastustuskykyyn virtaamaan kosketuksessa saman materiaalin tai toisen nestekerrosten kanssa, ja se riippuu nesteen nopeudesta ja viskositeetista. Viskositeetti on nesteen liikkumiskestävyyden mittaus.

-Stokes kitka

Stokes -kitka on eräänlainen nesteen kitka, jossa viskoosiseen nesteeseen upotetut pallomaiset hiukkaset kokevat kitkavoiman, joka hidastaa sen liikettä nesteen molekyylien vaihtelun vuoksi.

Stokes kitka [kirjoittanut Kraaiennest (https: // commons.Wikimedia.org/wiki/tiedosto: stokes_sphere.Svg)]

Virtaus on laminaarinen, kun viskoosit voimat, jotka vastustavat nesteen liikkumista, ovat suurempia kuin inertiaaliset voimat ja neste liikkuu riittävän pienellä nopeudella ja suoraviivaisella radalla.

Kitkakertoimet

Ensimmäisen kitkalain mukaan Coulomb Kitkakerroin μ Se saadaan kitkavoiman ja normaalin voiman välisestä suhteesta kosketuspintaan.

μ = f_{r -}-N

Kerroin μ Se on ulottumaton määrä, koska se on kahden voiman välinen suhde, joka riippuu kosketuksessa olevien materiaalien luonteesta ja käsittelystä. Yleensä kitkakertoimen arvo on välillä 0 ja 1.

Staattinen kitkakerroin

Staattinen kitkakerroin on vakio suhteellisuudesta, joka on voiman välillä, joka estää kehon liikkumisen kosketustilassa kosketuspinnalla ja normaali voima pintaan.

μ_ja= F_keksin/N

Kineettinen kitkakerroin

Kineettinen kitkakerroin on vakio suhteellisuudesta, joka on voiman välillä, joka rajoittaa pinnalla liikkuvan kehon liikkumista ja normaalia voimaa pintaan.

μ_c= F_RC/N

Staattinen kitkakerroin on suurempi kuin kineettinen kitkakerroin.

μ_s> μ_c

Joustava kitkakerroin

Joustava kitkakerroin on peräisin elastisten, pehmeiden tai karkeiden materiaalien kosketuspintojen välisestä kitkasta, jotka levitetyt voimat muodostuvat. Kitka vastustaa kahden elastisen pinnan välistä suhteellista liikettä ja siirtymistä liittyy materiaalin pintakerrosten joustava muodonmuutos.

Näissä olosuhteissa saatu kitkakerroin riippuu pinnan karheuden asteesta, kosketusmateriaalien fysikaalisista ominaisuuksista ja kuulovoiman tangentiaalisen komponentin suuruudesta materiaalirajapinnassa.

Molekyylinen kitkakerroin

Molekyylisen kitkakerroin saadaan voimasta, joka rajoittaa hiukkasen liikkumista, joka liukuu pehmeälle pinnalle tai nesteen läpi.

Kuinka kitka lasketaan?

Kiinteän rajapinnan kitkavoima lasketaan yhtälöllä F_{r -} = μn

N Se on normaali voima ja μ Se on kitkakerroin.

Joissakin tapauksissa normaali voima on yhtä suuri kuin kehon paino P. Paino saadaan kertomalla massa m kehon painovoiman kiihtyvyyden vuoksi g.

P= mg

Korvaamalla painoyhtälö kitkavoimayhtälössä, se saadaan:

Se voi palvella sinua: keskimääräinen kiihtyvyys: miten se lasketaan ja ratkaistaan

F_{r -} = μmg

Normaalit ominaisuudet

Kun esine on levossa tasaisella pinnalla, normaali voima on se, joka käyttää kehon pintaa ja vastustaa painovoiman vuoksi voimaa, Newtonin toiminta- ja reaktiolain mukaan.

Normaali voima toimii aina kohtisuorassa pintaan. Kaltevalla pinnalla normaali pienenee, kun kallistuskulma kasvaa ja pisteitä kohtisuoraan pois pinnasta, kun taas painopisteet pystysuoraan alaspäin. Normaali voimayhtälö kaltevalla pinnalla on:

N = mgcosθ

θ = kosketuspinnan kallistuskulma.

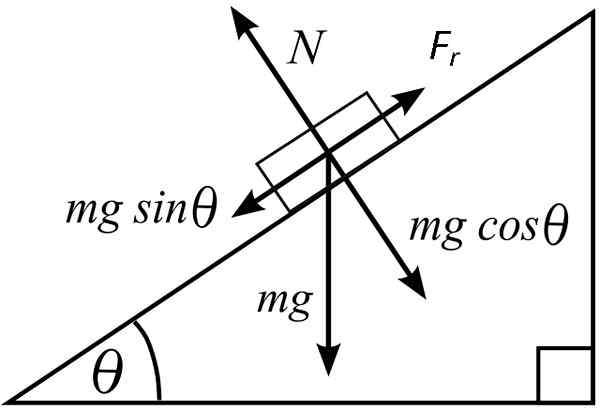Kitka kaltevassa tasossa [kirjoittanut METS501 (https: // commons.Wikimedia.org/wiki/tiedosto: vapaa_body.Svg)]

Kehoon toimivaan voiman komponentti se on:

F = mgsenθ

Kun sovellettu voima kasvaa kitkavoiman maksimiarvoon, tämä arvo vastaa staattista kitkavoimaa. Kun  F = f_keksin, Staattinen kitkavoima on:

F_keksin= mgsenθ

Ja staattinen kitkakerroin saadaan kaltevuuskulman tangentilla θ.

μ_ja = tanθ

Ratkaisut

-Kohteen kitkavoima, joka lepää vaakasuuntaisella pinnalla

Vaakapinnalle asetettu 15 kg: n laatikko työntää henkilö, joka kohdistaa 50 Newtonin voimaa pintaa pitkin ja levittää sitten 25 N -voima pitääksesi laatikon liikkeessä vakiona nopeudella. Määritä staattiset ja kineettiset kitkakertoimet.

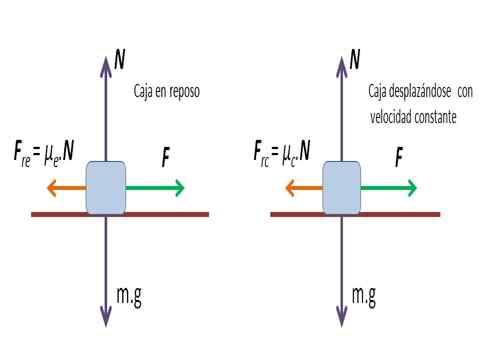Laatikko, joka liikkuu vaakasuuntaisella pinnalla

Ratkaisu: Sovelletun voiman arvolla laatikon siirtämiseen saadaan staattinen kitkakerroin μ_ja.

μ_ja= F_keksin/N

Normaali voima N pintaan on yhtä suuri kuin laatikon paino, niin N = m.g

N = 15 kgx9,8m/s²

N = 147New

Tässä tapauksessa, μ_ja= 50New/147New

μ_ja= 0,34

Käytetty voima vakiolaatikon nopeuden ylläpitämiseksi on kineettinen kitkavoima, joka on yhtä suuri kuin 25 -vuotias.

Kineettinen kitkakerroin saadaan yhtälöllä μ_c= F_RC /N

μ_c= 25New/147New

μ_c= 0,17

-Esineen kitkavoima voiman vaikutuksesta, jolla on kaltevuuskulma

Mies kohdistaa voiman 20 kg: n laatikkoon, jonka levityskulma on 30 °, suhteessa pintaan, jossa hän lepää. Mikä on käytetyn voiman suuruus laatikon siirtämiseen, jos laatikon ja pinnan välinen kitkakerroin on 0,5?

Ratkaisu: Käytetty voima ja sen pystysuora ja vaakasuora komponentit ovat esitetty vapaassa kehon kaaviossa.

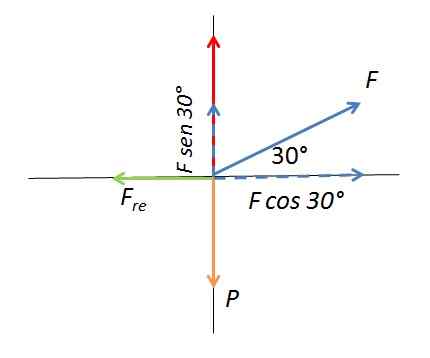Vapaakappalekuva

Käytetty voima muodostaa 30 ° kulman vaakasuoran pinnan kanssa. Voiman pystysuuntainen komponentti lisää normaalia voimaa, joka vaikuttaa staattiseen kitkavoimaan. Laatikko liikkuu, kun käytetyn voiman vaakasuora komponentti ylittää kitkavoiman maksimiarvon F_keksin. Yhdistämällä voiman vaakasuora komponentti staattisen kitkan kanssa, se saadaan:

F_keksin = Fcosθ                       [1]

F_keksin= μ_ja.N                          [2]

Se voi palvella sinua: Rutherford Atomic -malli: Historia, kokeet, postulaatit

μ_ja.N = fcosθ                      [3]

normaali vahvuus

Normaali voima ei ole enää kehon paino voiman pystysuuntaisen komponentin vuoksi.

Newtonin toisen lain mukaan pystysuoran akselin laatikkoon toimivien voimien summa on tyhjä, joten kiihtyvyyden pystysuuntainen komponentti on -lla_ja= 0. Normaali voima saadaan summasta

F sen30 ° + n - p = 0                      [4]

P = m.g                                        [5]

F snn 30 ° + n - m.G = 0                [6]

N = m.G - F Sen 30 °                      [7]

Kun korvataan yhtälö [7] yhtälössä [3], saadaan seuraava:

μ_ja. (m.G - f sin 30 °) = fcos30 °     [8]

Se puhdistuu F Yhtälöstä [8] ja saatu:

F = μ_ja . m.G /(cos 30 ° + μ_ja sin 30 °) = 0,5 x 20 kg x 9,8 m/s² / (0,87+ (0,5 x 0,5)) =

F = 87,5 -

-Kitka liikkuvassa ajoneuvossa

1,5 tonnia ajoneuvo liikkuu suoraviivaisella ja vaakasuoralla tiellä nopeudella 70 km/h nopeudella. Kuljettaja visualisoi tietyn etäisyyden esteet tiellä, joka pakottaa hänet lopettamaan voimakkaasti. Pysäytettynä luisteluajoneuvon lyhyen ajan, kunnes se pysähtyy. Jos renkaiden ja tien välinen kitkakerroin on 0,7; Määritä seuraava:

1. Mikä on kitkan arvo patina -ajoneuvon aikana?
2. Ajoneuvon hidastuminen
3. Ajoneuvon kulkeva etäisyys pysähdyksistä, kunnes se pysähtyy.

Ratkaisu-

Osa A

Vapaa kehon kaavio näyttää voimat, jotka toimivat ajoneuvoon luisteluun.

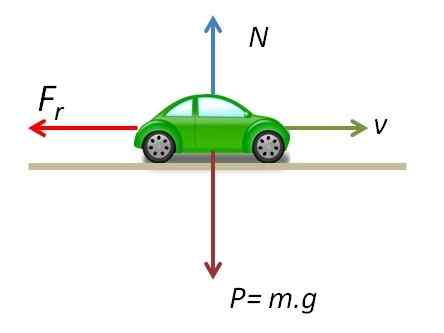Liikkuvassa ajoneuvossa toimivat voimat

Koska pystysuoraan akselilla toimivia voimia on nolla, normaali voima on yhtä suuri kuin ajoneuvon paino.

N = m.g

M = 1,5 tonnia = 1500 kg

N = 1500 kgx9,8m/s²= 14700NEW

Ajoneuvon kitkavoima luisteluun on:

F_{r -} = μn = 0,7x14700New

= 10290 UUSI

Osa B

Kitkavoima vaikuttaa ajoneuvon nopeuden vähentymiseen luisteluun.

Kun soveltaa Newtonin toista lakia, hidastumisen arvo saadaan puhdistamalla yhtälö F = m.-lla

A = f/m

A = (-10290 uusi)/ 1500 kg

= -6,86m/s²

Kohta C

Alkuperäinen ajoneuvon nopeus on v_{0 -} = 70 km/h = 19,44 m/s

Kun ajoneuvo pysäyttää lopullisen nopeutensa, se on v_F = 0 Ja hidastuminen on A = -6,86m/s²

Ajoneuvon kuljettama matka, koska se pysähtyy, kunnes se pysähtyy, se saadaan puhdistamalla d -d seuraavista yhtälöstä:

v_F² = v_{0 -}²+2Ad

D = (v_F² - v_{0 -}²)/2a

= ((0)²-(19.44m/s)²)/(2x (-6,86m/s²-A

D = 27,54 metriä

Ajoneuvo kulkee 27.54m Etäisyys ennen pysähtymistä.

 Viitteet

1. Kitkakerroimen laskelmat joustavissa kosketusolosuhteissa. Mikhin, n m. 2, 1968, Neuvostoliiton materiaalitiede, vol. 4, p. 149-152.
2. Blau, p J. Kitkatiede ja tekniikka. Florida, Yhdysvallat: CRC Press, 2009.
3. Tarttumisen ja kitkavoimien välinen suhde. IsraLachvili, J N, Chen, You-Lung ja Yoshizawa, H. 11, 1994, Journal of Adheesion Science and Technology, Vol. 8 p. 1231-1249.
4. Zimba, J. Voima ja liike. Baltimore, Maryland: The Johns Hopkins University Press, 2009.
5. Bhushan, b. Tribologian periaatteet ja sovellukset. New York: John Wiley ja pojat, 1999.
6. Sharma, C S ja Purohit, K. Mekanismien ja koneiden teoria. Uusi Delhi: Intian Prentice Hall, 2006.