Joustava voima mitä koostuu, kaavat ja harjoitukset

Se joustava voima Se on voima, jota esine käyttää vastustamaan muodon muutosta. Se ilmenee esineessä, jolla on taipumus palauttaa muodonsa, kun se on muodonmuutosvoiman alainen.

Joustava voimaa kutsutaan myös palauttavaksi voimaksi, koska se vastustaa muodonmuutoksia palauttaakseen esineitä tasapainoasentoon. Joustavan voiman siirto tapahtuu hiukkasten kautta, jotka integroivat esineet.

Kevään joustava lujuus

Esimerkiksi, kun metallinen jousi puristetaan, jousihiukkasia työntämä voima kohdistetaan vähentämällä niiden välistä erottelua samanaikaisesti hiukkasten vastustuskykyä työntämällä voimaa, joka on ristiriidassa puristuksen vastaisesti.

Jos jousen puristamisen sijasta se heitetään, venytetään, sen integroivat hiukkaset erotetaan enemmän. Samoin hiukkaset kestävät venytyksen vastaisen voiman erottamisen.

Kohteita, joilla on ominaisuus palauttaa alkuperäisen muodonsa vastaamuotovoiman vastakkain, kutsutaan joustaviksi esineiksi. Jouset, joustavat kumi- ja elastiset jouset ovat esimerkkejä joustavista esineistä.

[TOC]

Mikä on joustava voima?

Joustava voima (F_{k -k -};.

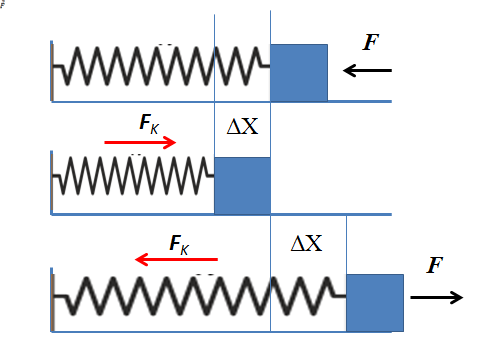
Joustavan voiman analysoimiseksi otetaan huomioon ihanteellinen jousimassajärjestelmä, joka koostuu vaakasuorasta asetetusta jousta, joka on toisessa päässä seinällä ja toisessa päässä halveksittavan massan lohkolle. Muita järjestelmään vaikuttavia voimia, kuten kitka tai painovoima, ei oteta huomioon.

Se voi palvella sinua: Toinen tasapainotila: Selitys, esimerkit, harjoitukset

Jos taikinassa käytetään vaakasuuntaista voimaa, joka on suunnattu kohti seinää, se siirretään jousen puristamiseen. Kevät siirtyy tasapainoasennostaan ​​kohti uutta sijaintia. Kun esine on taipumus pysyä tasapainossa, joustava voima ilmenee keväällä, joka vastustaa käytettyä voimaa.

Siirtymä osoittaa, kuinka paljon jousi ja joustava voima on muodonmuutos on verrannollinen siihen siirtymään. Kun jous on puristettu, aseman vaihtelu kasvaa ja lisää siten joustavaa voimaa.

Mitä enemmän jousi on pakattu, sitä enemmän oppositiovoimaa kohdistuu, kunnes se saavuttaa pisteen, jossa käytetty voima ja joustava voima ovat tasapainossa, joten jousimassajärjestelmä lakkaa liikkuvan. Lopettamalla lujuuden levittäminen Ainoa vaikuttava voima on joustava voima. Tämä voima kiihdyttää jousta muodonmuutoksen vastaisesti, kunnes tasapainon tila palauttaa.

Samalla tavalla se tapahtuu venytettäessä jousta tarkkailemalla taikinaa vaakasuoraan. Jousi venytetään ja välittömästi saa voiman, joka on verrannollinen siirtymään vastustamaan venyttämistä.

Kaavat

Joustava voimakaava ilmaistaan ​​Hooken lailla. Tämä laki osoittaa, että esineen aiheuttama lineaarinen elastinen voima on verrannollinen siirtymiseen.

F_{k -k -} = -K.Δs         [1]

F_{k -k -} = Joustava voima

k -k - = Suhteellisuusvakio

Δs = Siirtymä

Kun esine liikkuu vaakasuoraan, kuten seinämän kohteena olevan jousen tapauksessa, siirtymä on Δx, Ja Hooken lain ilmaisu on kirjoitettu:

F_{k -k -} = -K.Δx        [2]

Voi palvella sinua: konvergenssilinssi: Ominaisuudet, tyypit ja liikunta on ratkaistu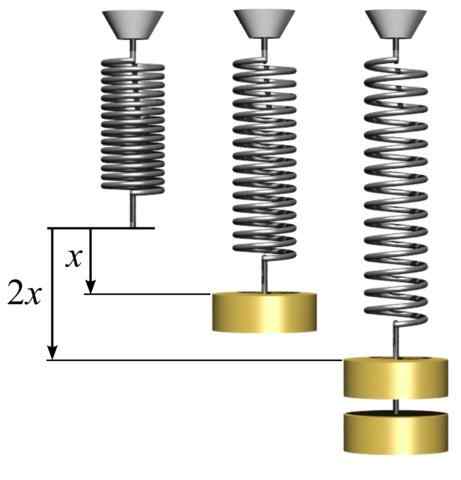Hooken laki. Joustava voima verrannollinen venytys. [Kirjoittanut svjo (https: // commons.Wikimedia.org/wiki/tiedosto: koukkuja.Png)]

Yhtälön negatiivinen merkki osoittaa, että jousen joustava voima on vastakkaiseen suuntaan kuin siirtymä aiheuttanut voima. Suhteellisuusvakio k -k - Se on vakio, joka riippuu siitä materiaalityypistä, johon jousi muodostuu. Vakion yhtenäisyys k -k - On N/m.

Joustavilla esineillä on joustavuusraja, joka riippuu muodonmuutosvakiosta. Jos se ulottuu elastisen rajan yli, se muodonmuutos pysyvästi.

Yhtälö [1] ja [2] koskevat pieniä jousensiirtymiä. Kun siirtymät ovat suurempia, termit lisätään suuremmalla voimalla Δx.

Kineettinen energia ja potentiaalienergia viittasivat joustavaan voimaan

Joustava voima toimii keväällä siirtämällä sitä kohti tasapainoa. Prosessin aikana jousimassajärjestelmän potentiaalinen energia kasvaa. Elastisen voiman tekemästä työstä johtuva potentiaalinen energia ilmaistaan ​​yhtälössä [3].

U = ½ k .  ΔX²[3]

Potentiaalinen energia ilmaistaan ​​Joulesissa (J).

Lopettamalla muodonmuutosvoiman asettaminen, jousi kiihtyy tasapainoasentoon vähentämällä potentiaalienergiaa ja lisäämällä kineettistä energiaa.

Jousimassajärjestelmän kineettinen energia, kun tasapainopaikka saavuttaa, määritetään yhtälöllä [4].

JA_{k -k -}= ½ m.v²[4]

m = massa

v = keväänopeus

Kevään massajärjestelmän ratkaisemiseksi Newtonin toista lakia sovelletaan ottaen huomioon, että elastinen voima on muuttuva voima.

Käytännön esimerkkien harjoitukset

Muodonmuutosvoiman saaminen

Kuinka paljon voimaa on tarpeen jousille levitettäväksi 5 cm: n venyttämiseen, jos jousvakio on 35N/M?

Voi palvella sinua: Painovoiman kiihtyminen: Mikä se on, miten se mitataan ja harjoitukset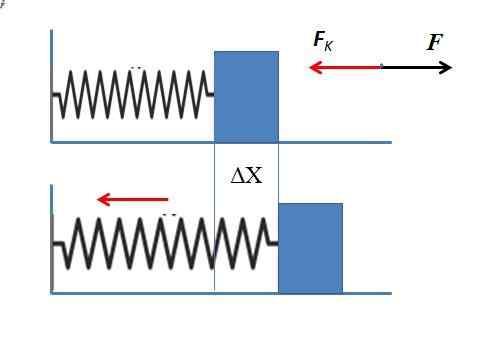Joustavan jousen joustava voima, joka venyttää 5 cm

Koska levitysvoima on vastustanut joustavaa voimaa määritetään F_{k -k -} Olettaen, että jousi on venytetty vaakasuoraan. Tulos ei vaadi negatiivista merkkiä, koska sovellusvoimaa tarvitaan vain.

Hooken laki

F_{k -k -} = -K.ΔX       

Vakio k -k - keväästä on 35N/M.

Δx = 5cm = 0,05m

F_{k -k -} = -35n/m . 0,05m

F_{k -k -} = - 1,75N = - F

Tarvittu 1,75 n voimaa muodonmuutos keväällä 5cm.

Muodonmuutosvakion saaminen

Mikä on joustavan jousen muodonmuutosvakio 20 cm voimalla 60N?

ΔX =20 cm = 0,2 metriä

F = 60N

F_{k -k -} = -60N = - F

K = - f_{k -k -} / Δx

  = -(-60N) /0,2m

K = 300 N/m

Keväänvakio on 300N/M

Potentiaalisen energian saaminen

Mikä on potentiaalinen energia, joka viitataan pakatun jousen joustavan voiman tekemässä työssä 10 cm Ja sen muodonmuutosvakio on 20n/m?

Δx =10 cm = 0,1m

K = 20 n/m

F_{k -k -} = -20N/M . 0,1m

F_{k -k -} = -200n

Kevään joustava voima on -200n.

Tämä voima toimii keväällä siirtääkseen sitä kohti tasapainoa. Tätä työtä suoritettaessa järjestelmän potentiaalinen energia kasvaa.

Potentiaalienergia lasketaan yhtälöllä [3]

U = ½ k .  ΔX²

U = ½ (20n/m) . (0,1 m)²

U = 0,1joules

Viitteet

1. Kittel, C, Knight, W D ja Ruderman, M A. Mekaniikka. Yhdysvallat: MC Graw Hill, 1973, vol. Yllyttää.
2. Rama Reddy, K, Badami, S B ja Balasubramanian, V. Oskillamentit ja aallot. Intia: University Press, 1994.
3. Murphy, J. Fysiikka: aineen ja energian ominaisuuksien alistaminen. New York: Britannica Educational Publishing, 2015.
4. Giordano, n J. Yliopistofysiikka: päättely ja suhteet. Kanada: Brooks/Cole, 2009.
5. Walker, J, Halliday, D ja Resnick, R. Fysiikan perusteet. Yhdysvallat: Wiley, 2014.