Kasvava toiminto Kuinka tunnistaa se, esimerkkejä, harjoituksia

Sinulla on yksi kasvava toiminta Kun Y: n arvo kasvaa.

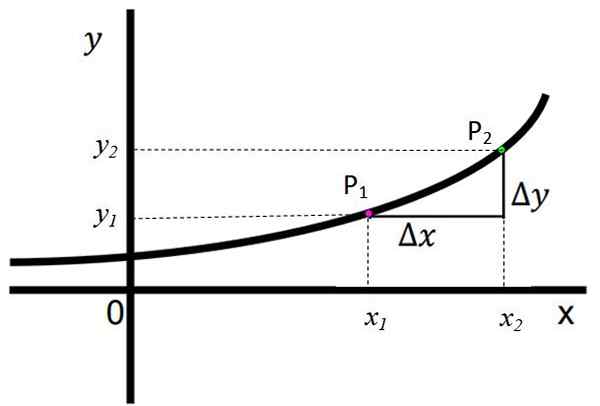
Seuraava kuva näyttää kasvavan funktion, ja selvästi havaitaan, että siirtyessäsi vasemmalta oikealle X -akselilla, vastaavan koordinaatin arvo ja vastaa F (x), kasvaa vähitellen asteittain. Sanotaan, että jos kaikesta x₂ > x₁, Sitten se on olemassa ja₂ > ja₁.

Kuvio 1. Kasvava toiminto. Lähde: f. Zapata.

Kohdat p₁ Ja p₂ Ne on osoitettu, heillä on vastaavasti koordinaatit (x₁, ja₁) ja (x₂,ja₂-A. Ne on määritelty:

Δy = y₂ -ja₁

Δx = x₂ -x₁

Tässä toiminnossa sekä ΔY: llä että ΔX: llä on positiivinen merkki, mikä tarkoittaa sitä ja₂ > ja₁ ja x₂ > x₁, vastaavasti. Tämä on selvä merkki siitä, että funktio kasvaa tehokkaasti.

Hyvä esimerkki aina kasvavasta toiminnasta (kasvava yksitoikkoinen) on todellisen määrän Neperian logaritmi. Mitä suurempi luku, sitä suurempi sen logaritmi.

[TOC]

Kuinka tunnistaa kasvava toiminto?

Yksinkertaisessa ja jatkuvassa toiminnassa kuvassa 1 esitetyllä tavalla on helppo määrittää, kasvaako toiminto vai pienenee, edellyttäen, että kaavio on käytettävissä.

Monimutkaisemmat toiminnot voivat kuitenkin kasvaa tietyin väliajoin ja vähentyä toisissa. Siksi puhumme Kasvuvälit ja vähentää funktio.

Verkossa on ilmaisia ​​online -grafiikoita, kuten geogebra, jotka sallivat kaikenlaisten toimintojen piirtämisen. Kaaviolla on helppo määrittää, kasvaako toiminto aina, kuten f (x) = log x vai onko siinä väliajoja, joissa se kasvaa, ja muut, joissa se pienenee ja mitä on.

Ensimmäisen johdannaisen kriteeri

Kun otetaan huomioon tietty numeerinen aika I, jos määrien Δy ja ΔX välinen osuus on positiivinen, funktio kasvaa. Ja päinvastoin, jos se on negatiivinen, funktio pienenee.

Se voi palvella sinua: Taajuuden todennäköisyys: Konsepti, miten se lasketaan ja esimerkkejä

Sinun täytyy:

ΔY / Δx> 0 → Kasvava funktio

Sitä, että ΔY / Δx> 0 ja funktio kasvaa tietyssä aikavälillä, viittaa siihen, että funktion ensimmäistä johdettua tai pikemminkin sen merkkiä voidaan käyttää kriteerinä sen määrittämiseksi, kasvaako funktio tietyssä tietyllä aikaväli tai jopa verkkotunnuksen tietyssä vaiheessa.

Itse asiassa ensimmäinen johdannainen määritellään käyrän kaltevuuteen jokainen piste:

Mikä tarkoittaa, että ΔX voidaan tehdä niin pieni kuin haluat. Jos f '(x)> 0 tietylle x -arvolle, esimerkiksi x = a, käyrän kaltevuus siinä vaiheessa f' (a) on positiivinen ja funktio kasvaa siellä.

Seuraava lause tarjoaa kriteerin tietää, milloin funktio kasvaa aikavälillä (a, b):

Lause

Olkoon f (x) johdettava funktio kohdassa (a, b). Jos f '(x)> 0, jokaiselle mainitulle aikavälille kuuluvan x: n arvolle sanotaan, että f (x) kasvaa (a, b).

Lause sovelletaan selvittämään, missä välissä funktio kasvaa näiden vaiheiden seurauksena:

Vaihe 1

Löydä pisteitä, joissa f '(x) = 0, samoin kuin pisteitä, joissa f' (x) ei ole olemassa. Näitä kutsutaan kriittiset kohdat, Nämä ovat pisteitä, joissa f '(x) voi muuttaa merkkiä, ja siksi F (x): lla on mahdollisuus siirtyä kasvusta vähentymiseen tai päinvastoin.

Vaihe 2

Löydä f '(x): n merkki mielivaltaisesta arvosta jokaisessa vaiheessa 1 määritettyjen väliajojen perusteella, jotka on määritetty vaiheessa 1.

Vaihe 3

Käytä lausetta tietääksesi, kasvaako funktio vai ei jokaisella aikavälillä.

Esimerkkejä kasvavista toiminnoista

On toimintoja, joilla on joitain kasvuvälejä ja toiset vähenevät, mutta alla esitetyt ne kasvavat aina.

Paino ikään perustuva

Henkilön paino sen syntymisen jälkeen, kunnes nuoruus päättyy, on melkein aina kasvava ikä. Vauvat ja lapset kasvavat ja kehittyvät vuosien varrella, ja sitten heidän aikuisuuden saavuttaessa loppuelämänsä odotetaan ylläpitävän vakaa paino, vaikka ylä- ja alamäet ovat hyvin usein.

Voi palvella sinua: Pystysuora viiva

Logaritmitoiminto

Todellisen muuttuvan logaritmin neperian f (x) = ln x ja desimaalin logaritmi f (x) = log x toiminnot kasvavat aina.

Todellisen numeron neliöjuuren funktio

Toinen kasvava toiminto on positiivisen reaalilukun neliöjuuren funktio:

y = √x

Liittyvä funktio ja lineaarinen funktio

Aiheeseen liittyvä toiminto:

f (x) = mx + b

Se kasvaa aina, kun linja on positiivinen kaltevuus. Samoin identiteetti- ja lineaariset toiminnot:

f (x) = x ja f (x) = AX, A> 0: lla

He kasvavat kaikilla verkkotunnuksillaan.

Eksponentiaalinen funktio

Eksponentiaalinen funktio, kuten f (x) = e^x  Ja yleensä muodon toiminta:

f (x) = a^x, > 1

He kasvavat kaikilla verkkotunnuksillaan.

Potentiaalinen Impara -indeksitoiminto

Odd Exponentin mahdolliset toiminnot, kuten nämä:

• f (x) = x³
• g (x) = x⁵

Ne kasvavat aina.

Harjoitukset

Harjoitus 1

Määritä, millä välein seuraavassa kaaviossa esitetty funktio kasvaa:

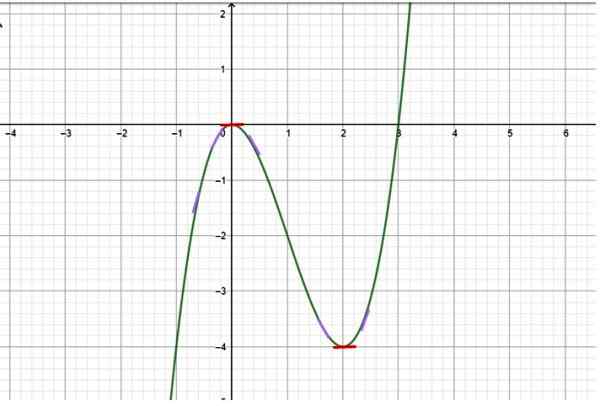Kuva 2. Toiminta kasvulla ja pienenemisväleillä. Lähde: f. Zapata.

Ratkaisu

Koska kaavio on käytettävissä, sen huolellisesta havainnosta määritetään, että funktiolla on seuraava käyttäytyminen:

-X → -∞: sta x = 0 funktio kasvaa, koska y: n arvot muuttuvat vähemmän ja vähemmän negatiivisiksi. Pienet kaltevuussegmentit on piirretty violetiksi osoittamaan tangenttiviivan kaltevuus käyrälle eri kohdissa (käyrän tangentin kaltevuus on juuri sen ensimmäinen johdannainen).

Näillä segmenteillä on positiivinen kaltevuus, joten lause varmistaa, että funktio kasvaa tällä aikavälillä.

-Mutta kohdassa x = 0 käyrän kaltevuus peruutetaan, mikä on merkitty pienellä vaakasuoralla punaisella segmentillä. Tämä on Kriittinen piste toiminnasta.

Voi palvella sinua: mitkä ovat matematiikkaa ja mitä ne ovat? 7 tärkeää sovellusta

Sieltä funktio alkaa vähentyä, ja siitä tulee negatiivisempia arvoja ja. Tämä tilanne jatkuu, kunnes x = 2, mikä on toinen kriittinen kohta.

Sitten, välillä x = 0 - x = 2 funktio pienenee.

-X = 2: sta funktio muuttuu vähemmän ja vähemmän negatiiviseksi, kunnes x = 3 ylittää x -akselin ja muuttuu edelleen positiivisemmaksi joka kerta. Siksi tämä on kasvuväli.

Johtopäätös: Kasvuvälit ovat (-∞, 0) ja (2, ∞+), kun taas laskuväli on (0,2).

Harjoitus 2

Määritä seuraavan funktion kasvuvälit ensimmäisen johdannaisen kriteerien kautta:

f (x) = x² - 2x

Ratkaisu

Edellä esitettyjen vaiheiden jälkeen ensimmäinen johdannainen lasketaan ja on yhtä suuri kuin 0 kriittisten pisteiden löytämiseksi:

f '(x) = 2x -2

2x - 2 = 0

x = 1

Tämä arvo määrittää väliajojen olemassaolon (-∞, 1) ja (1, ∞+). Valittu kaksi mielivaltaista arvoa, jotka kuuluvat jokaiselle:

-X = 0, joka kuuluu (-∞, 1), sinun on f '(0) = 2.0 - 2 = -2. Koska tulos on negatiivinen, funktio laskee tällä aikavälillä.

-X = 3: lle, joka kuuluu (1, ∞+), ensimmäinen johdannainen on F '(3) = 2: n arvoinen.3 - 2 = 4. Koska tulos on positiivinen, päätellään, että funktio kasvaa tällä aikavälillä.

Lukija voi piirtää alkuperäisen toiminnon f (x) = x² - 2x online -grafiikassa tämän tuloksen vahvistamiseksi.

Viitteet

1. Ayres, f. 2000. Laskeminen. 5DED. MC Graw Hill.
2. Leithold, L. 1992. Laskenta analyyttisellä geometrialla. Harla, S.-Lla.
3. Purcell, E. J -., Varberg, D., & Rigdon, S. JA. (2007). Laskeminen. Meksiko: Pearson Education.
4. Matemobili. Toiminnot, kasvava, väheneminen ja vakio. Toipunut: Matemovil.com
5. Requena, b. Kasvavat toiminnot. Toipunut: UniversOformulat.com.
6. Stewart, J. 2006. Precculment: Laskentamatematiikka. Viides. Painos. Cengage -oppiminen.