Vähentävä toimintoa kuinka tunnistaa se, esimerkkejä, harjoituksia

Eräs vähentävä toiminto f on sellainen, jonka arvo laskee, kun x: n arvo kasvaa. Tarkoittaa, että tietyllä aikavälillä ottaen huomioon kaksi arvoa x₁ ja x₂ sellainen, että x₁ < x₂, sitten f (x₁)> f (x₂-A.

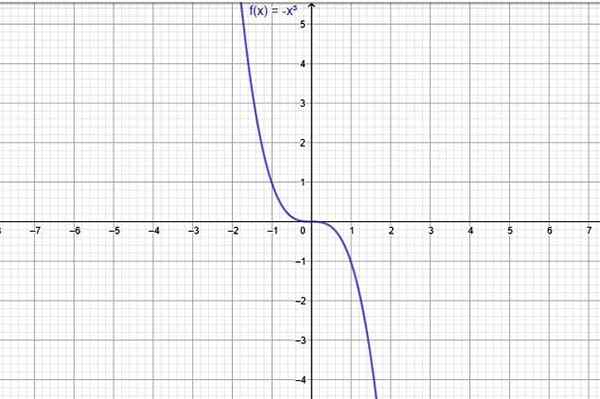
Esimerkki aina pienenemisestä on f (x) = -x³, jonka kaavio näyttää seuraavassa kuvassa:

Kuvio 1. Funktio, joka aina pienenee koko alueella, on f (x) = -x^3. Lähde: f. Zapata Geogebran kautta.

Vaikka joillekin tällaisille toiminnoille on ominaista väheneminen kaikessa alueellaan, kaikki eivät käyttäytyy näin, ne kasvavat ja myös ne, jotka kasvavat ja vähenevät tietyillä alueiden välillä. Kasvu- ja laskuvälien tutkimusta kutsutaan yksitoikkoisuus toiminnasta.

Samoin funktion kasvua tai laskua voidaan pitää tietyssä verkkotunnuspisteessä. Mutta mikä tahansa funktio, joka pienenee tietyssä aikavälillä, on myös jokaisessa vaiheessa, joka kuuluu siihen.

[TOC]

Kuinka tunnistaa vähentyvä toiminto?

Funktiokaavio osoittaa visuaalisesti, väheneekö se vai ei. Jos "laskeutuu" -funktioon siirtyessä X: n kasvavassa merkityksessä se tarkoittaa, että se vähenee.

Ja jos sinulla on väliajoja, joissa se pienenee ja kasvaa vuorotellen, mikä on tavallisinta, koska nämä paljastetaan selvästi tarkkailemalla funktion käyttäytymistä koko sen alueen ajan, koska toiminto "nousee" ja muut sisään mikä "laske".

Vaihtoehtoisesti, jos funktiokaaviota ei ole saatavana, analyyttisesti on mahdollista määrittää, pieneneekö se yhdessä pisteessä vai aikavälillä ensimmäisen johdannaisen kautta.

Ensimmäisen johdannaisen kriteeri

Huomaa kuvassa 2 esitetyn vähenevän funktion käyttäytyminen. Vaaleanpunaiset linjasegmentit ovat tangenttipisteitä, joiden koordinaatit ovat [a, f (a)] ja [A+H, F (A+H)] ja niillä on negatiivinen kaltevuus.

Voi palvella sinua: Kuinka kyselyssä saadut tiedot?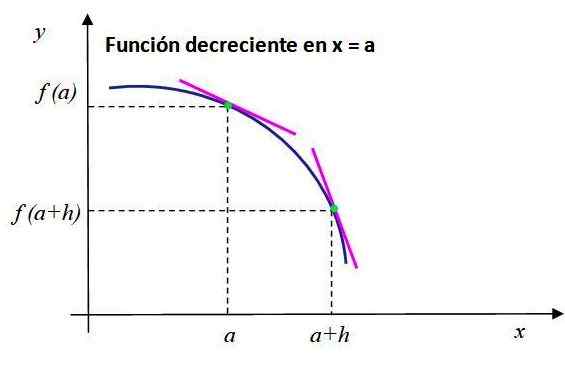Kuva 2. Tangenttiviivan kaltevuus f (x) -kaavioon on negatiivinen kohdassa x = a, sitten funktio pienenee tässä vaiheessa. Lähde: f. Zapata.

Tätä toimintoa varten seuraava on toteutettu:

F (A+H) - F (A) < 0 ⇒  F (A+H) < f (a)

Siksi voidaan ajatella, että funktio vähenee x = a.

Ensimmäinen johdettu funktiosta F (x), arvioidaan kuitenkin x = a: lla, joka on määritelmän mukaan tangentin viivan kaltevuus käyrän kohdalla x = a, annetaan:

Raja osoittaa, että H: n arvo voidaan tehdä niin pieni kuin haluat ja ehdottaa, että merkki fa), Sitä voidaan käyttää tietämään, pieneneekö funktio tietyssä kohdassa, kunhan johdannainen on siinä vaiheessa.

Sitten kyllä fa) < 0, Voidaan vakuuttaa, että funktio on vähenevä ja päinvastoin, jos f '(a)> 0, Sitten funktio kasvaa siinä vaiheessa.

Lause aleneville ja kasvaville toiminnoille

Aikaisemmin viitattiin funktion käyttäytymiseen pisteessä. Nyt seuraava lause sallii tietää välit, joissa funktio pienenee, kasvaa tai vakio:

Olkoon f erilainen funktio aikavälillä (a, b). Onko totta että:

-Kyllä f '(x) < 0 para todo x perteneciente a (a,b), entonces f(x) es decreciente en (a,b).

-Jos päinvastoin f '(x)> 0 kaikille X: lle, joka kuuluu (a, b), sanotaan, että funktio F (x) kasvaa (a, b).

-Lopuksi, jos f '(x) = 0 kaikille x: lle, joka kuuluu aikaväliin (a, b), f (x) on vakio mainitussa aikavälillä.

Esittely

Oletetaan, että f '(x) < 0 para cualquier valor de x en el intervalo (a,b), además se tienen x₁ ja x₂ kuuluu mainittuun aikaväliin ja ehtoon, että x₁< x₂.

Keskimääräinen arvolause toteaa, että x: n välillä on reaaliluvus, x: n välillä₁ ja x₂, sellainen:

Voi palvella sinua: Yleinen tekijä ryhmittelyssä: Esimerkkejä, harjoituksia

Kuten x: n jälkeen x₁< x₂,  ΔX on positiivinen. Joten, koska f '(c) on negatiivinen, niin myös ΔY on. Siksi f (x₁-A on suurempi kuin f (x₂-A Ja funktio vähenee tehokkaasti kaikissa kohdissa (a, b).

Vaiheet tietää, onko funktio vähentynyt

Näitä vaiheita noudatetaan funktion vähenemis- ja kasvuvälit funktion väliajoja soveltamalla edellistä lausetta:

-Etsi ensimmäinen johdettu toiminnosta ja sovita se nollaan ratkaisemalla tuloksena oleva yhtälö. Määritä myös pisteet, joissa johdannaista ei ole.

Kaikkia näitä kohtia kutsutaan kriittiset kohdat Ja ne on välttämätöntä löytää, koska heissä johdannaisella on mahdollisuus muuttaa merkkiä, mikä osoittaa, että funktio siirtyy laskusta vähentymiseen tai päinvastoin.

-Funktion alue on jaettu väliajoihin, jotka määritetään pisteillä, joissa ensimmäinen johdannainen peruutetaan tai sitä ei ole olemassa.

-Lopuksi johdannaisen merkkiä tutkitaan mielivaltaisessa pisteessä, joka kuuluu jokaiseen edellisessä vaiheessa saatuun väliajoin.

Esimerkkejä alenevista toiminnoista

Toiminnot eivät kaikki vähene samalla nopeudella, jotkut tekevät sen nopeammin kuin toiset. Seuraavat toiminnot, jotka ilmestyvät usein käytännössä, vähenevät:

Eksponentiaalinen funktio

Muodon f (x) = a funktio^x, Välillä on välillä 0 - 1, lukuun ottamatta näitä, vähenee nopeasti koko verkkotunnuksensa.

Toiminto 1/x

Online -graafisen ohjelman kautta geogebrana rakennetaan funktion f (x) = 1/x kuvaaja, mikä vahvistaa, että se pienenee koko verkkotunnuksessaan.

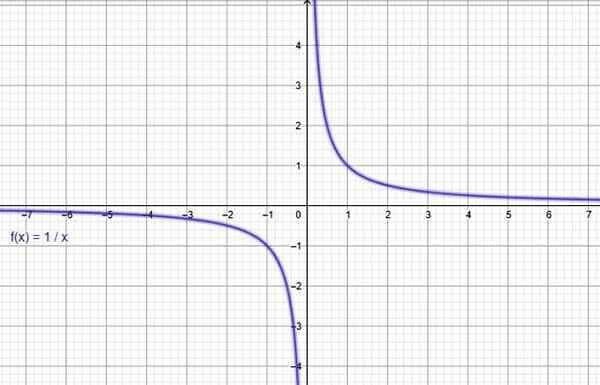Kuva 3. Funktio f (x) = 1/x pienenee. Lähde: f. Zapata Geogebran kautta.

Aiheeseen liittyvä funktio

Muodon y = mx + b toiminnot m: n kanssa<0 tienen gráficas que son rectas de pendiente negativa y por lo tanto son funciones decrecientes.

Voi palvella sinua: matemaattinen tasa -arvo

Liikuntaa

Löydä, jos sellaista on, funktion vähenemisvälit:

f (x) = x⁴ - 6x² - 4

Ratkaisu

Ensimmäinen askel on löytää f '(x)-

f '(x) = 4x³ - 12x

F (x): n ensimmäinen johdannainen on jatkuva funktio, ts. Sillä ei ole epäjatkuvuuspisteitä, mutta se peruutetaan:

4x³ - 12x = 0 = 4x (x²-3) = 0

Tämän yhtälön ratkaisut ovat: x₁ = 0, x₂ = - √3 ja x₃ = √3. Nämä ovat kriittisiä kohtia, jotka jakavat f (x) -alueen välein: (-∞,- √3); (- √3.0); (0, √3); (√3, ∞+).

Sitten arvioidaan ensimmäinen mielivaltainen X -arvo, joka kuuluu jokaiselle aikavälille. Nämä arvot valittiin:

For (-∞,- √3)

F '(-2) = 4 (-2)³ - 12x (-2) = -32+24 = -8

For (- √3.0)

F '(-1) = 4 (-1)³ - 12x (-1) = -4+12 = 8

For (0, √3)

f '(1) = 4 (1)³ - 12x (1) = 4-12 = -8

For (√3, ∞+)

f '(2) = 4 (2)³ - 12x (2) = 32-24 = 8

Kuten useita välejä, on hyvä idea tehdä taulukko tulosten järjestämiseksi. Ylöspäin suuntautuva nuoli osoittaa, että funktio kasvaa ja alas, mikä vähenee:

Johtopäätöksenä on, että funktio vähenee väliajoin (-∞,- √3) ja (0, √3) ja kasvaa jäljellä olevilla väliajoin. Geogebran alkuperäinen toiminto tarkistetaan helposti graafimalla.

Viitteet

1. Ayres, f. 2000. Laskeminen. 5DED. MC Graw Hill.
2. Leithold, L. 1992. Laskenta analyyttisellä geometrialla. Harla, S.-Lla.
3. Purcell, E. J -., Varberg, D., & Rigdon, S. JA. (2007). Laskeminen. Meksiko: Pearson Education.
4. Matemobili. Toiminnot, kasvava, väheneminen ja vakio. Toipunut: Matemovil.com
5. Stewart, J. 2006. Precculment: Laskentamatematiikka. Viides. Painos. Cengage -oppiminen.