Porrastetut funktioominaisuudet, esimerkit, harjoitukset

Se porrastettu toiminta y = s (x) on kappaleina tai osilla määritelty funktio siten, että äärellisellä aikavälillä [a, b] sillä on rajallinen määrä epäjatkuvuuksia, joita kutsumme x_{0 -} < x₁ < x₂ <… . x_n.  Jokaisella avoimella aikavälillä (x_Yllyttää , x_I+1), ja sillä on vakioarvo arvo_Yllyttää, Epäjatkuvuuksilla -saltos- pisteissä x_Yllyttää.

Kaavio, joka johtuu tällaisesta toiminnosta, koostuu vaiheista tai vaiheista. Katsotaanpa alla olevaa esimerkkiä:

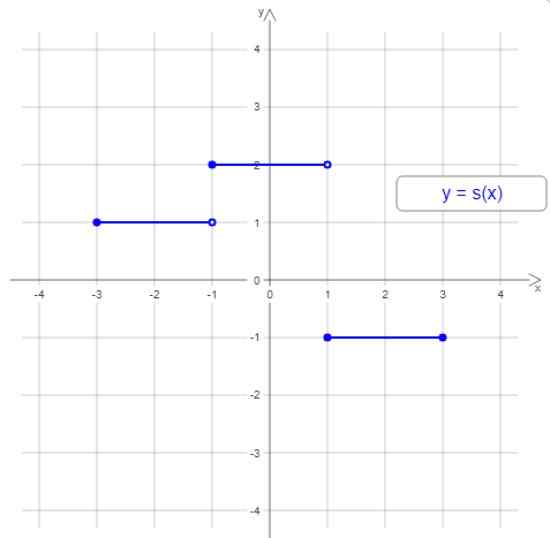
Kuvio 1. Esimerkki porrastetusta toiminnosta. Lähde: Wikimedia Commons.

Tämän askelfunktion kaaviossa on kolme vaihetta tai porrastettuja väliajoja, mutta yleensä porrastetulla toiminnolla voi olla minkä tahansa määrän vaiheita. Vaiheiden leveys voi olla erilainen ja portaikko ei aina nouse tai laskeva.

Esimerkin porrastettu funktio voidaan kirjoittaa määrittämällä kunkin vaiheen leveys ja korkea, kuten tämä:

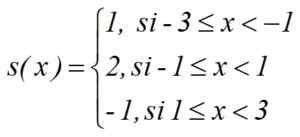
[TOC]

Askelfunktion ominaisuudet

-Toiminto vastaanottaa nimensä kaaviolla vaiheiden muodossa, sen muodostavien segmenttien antamat segmentit. Jokaisella segmentillä on osa funktion aluetta ja jokaisessa funktio on vakio.

-Porrastetun funktion alue ovat arvot, jotka kuuluvat aikavälille, jolle se on määritelty: [a, b], kun taas alue muodostuu arvojen s_Yllyttää vaiheiden korkeuksista.

Kuvion 1 esimerkissä domeeni on aikaväli [-3,3] ja alue on arvot -1, 1 ja 2.

-Porrastettu funktio on jatkuvaa lukuun ottamatta arvoja, jotka rajaavat jokaisen vaiheen, pisteet x_Yllyttää.

-Escalonada -toiminnot voidaan lisätä ja kertoa uusien vaiheiden toimintojen aiheuttamiseksi.

-Sen johdannainen on 0 pisteille, joissa se on määritelty, koska niissä funktio on vakio. Johdannaista ei ole epäjatkuvuuksissa.

-Askelfunktion s (x) integraali -lla ja b - Se on olemassa ja vastaa leveyden x suorakulmioiden alueiden summaa_Yllyttää- x_I-1 ja korkeus s_{k -k -}, yhtä suuri kuin askel.

Voi palvella sinua: Riippumattomat tapahtumat: esittely, esimerkit, harjoitukset

Koska suorakulmion alue on pohjan tuote korkeuden mukaan, meidän on:

Esimerkkejä porrastetuista toiminnoista

Porrastettujen toimintojen sisällä on useita tyyppejä, esimerkiksi koko osa ja toiminto Yhtenäinen askel, samoin kuin erilaisia ​​porrastettuja toimintoja, jotka kuvaavat yleisiä tilanteita, kuten monien palvelujen hinnat. Katsotaanpa joitain esimerkkejä:

- Esimerkki 1: Koko osapuolet

Koko osatoiminto käyttää usein kaksoiskiinnikettä:

f (x) = [[x]]

Ja se määritellään funktioksi, joka määrittää jokaiselle reaalilukulle lähin tai pienempi kokonaisluku, jättämättä huomiotta mitään, jolla on numero, jolla on numero. Tapauksen mukaan meillä on:

Katto- tai taivastoiminto

Määritä jokaiselle verkkotunnusarvolle lähinnä kokonaisluku ylimääräisesti. Esimerkiksi:

[[[[+2.56]]] = 3

0 desimaaliosaan jätetään huomiotta.56 ja lähin kokonaisluku on osoitettu, joka on suurempi kuin 2.

Toinen esimerkki:

[[[[-4.2]]= -3

Jälleen desimaaliosa 0 jätetään pois.2 ja suurin suurin kokonaisluku lähempänä -4: tä pidetään funktion arvona, joka on -3.

Seuraavassa kuvassa on kattofunktion kuvaaja, huomaa, että vaihe on rajattu pienellä ontolla ympyrällä vasemmalle ja yksi täynnä oikealle, koska mikä tahansa aikavälin määrä, suurin kokonaisluku on osoitettu päättyjen välillä. päättyy aikavälin päiden välillä.

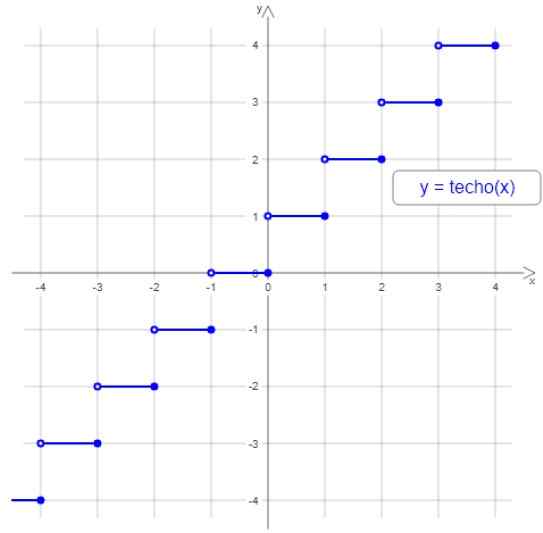Kuva 2. Katto- tai taivastoiminto. Lähde: Wikimedia Commons.

Esimerkiksi kaikille arvoille 3–4 on osoitettu koko 4, jotka ovat välillä -2 ja -1.

Lattia- tai maaperän toiminta

Määritä jokaiselle verkkotunnusarvolle lähin kokonaisluku oletusarvoisesti. Esimerkkejä tästä toiminnosta ovat:

Voi palvella sinua: kuinka monta kymmenesosaa on yksikössä?

[[+3.7]] = 3

[[-1.5]] = -2

[[π]] = 3

Molemmat toiminnot ovat jatkuvia lukuun ottamatta kokonaislukuja, joissa hyppy esitetään, ja se on vakio kokonaislukujen K ja K+1 välillä oleville arvoille.

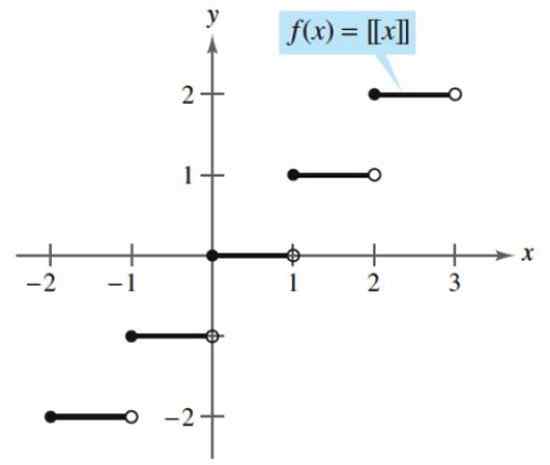Kuva 3. Lattia- tai maaperän toiminta. Lähde: Larson, R. Muuttujan laskenta.

- Esimerkki 2

Kaupungissa taksin hinta on 3.65 dollaria ensimmäisen 100 m. Ja jokaista 100 metriä on 0.18 dollaria on 50 km: n reittien raja.

Halustetaan perustaa toiminto, joka yhdistää reitin mittarina palvelun kustannuksiin $: lla, jolla on oltava tämä lomake:

f (x) = 3.65 + 0.18. [[x /100]] $

Missä koko osafunktio voi olla taivaan funktiosta, johon 3 on lisätty perustaajuus.65 dollaria. Esimerkiksi, jos haluamme tietää, kuinka paljon se maksetaan 6 -vuotiaasta.25 km = 6250 m, meillä on:

f (x) = 3.65 + 0.18. [[x /100]] $ = 3.65 + 0.18 . [[6250/100]] $ = 3.65 + [[11.25]] $ = 15.65 dollaria

Jos taksiyhtiö valitsee lattiatoiminnon, asiakas maksaa hiukan vähemmän matkasta:

f (x) = 3.65 + 0.18. [[x /100]] $ = 3.65 + 0.18 . [[6250/100]] $ = 3.65 + [[11.25]] $ = 14.65 dollaria

Ratkaisut

- Harjoitus 1

Kaupunkien A ja B välillä olevat pitkän matkan puhelut maksavat 0.40 dollaria 10 minuuttia. Tämän ajanjakson jälkeen murto -osa tai lisä minuutti on arvoinen 0.05 $.

Ilmaista puhelun kustannukset (t), joka kestää tietyn määrän minuuttia.

Ratkaisu

Voimme ilmaista tämän toiminnon, jos analysoimme, mitä jokaisella vaihtoehdolla tapahtuu puhelun ajan:

T ≤ 10 minuuttia

Kun T, joka on aika, että puhelu kestää, on vähemmän tai yhtä suuri kuin 10 minuuttia, maksetaan 0.40 dollaria.

Voi palvella sinua: 2 -Digit -divisioonat ratkaistu

Siksi:

f (t) = 0.40 dollaria T: stä, joka sisältyy välillä 0–10 minuuttia.

Meillä on jo osa toimintoa.

T> 10 minuutin ajan

Entero T -tapaus

Katsotaanpa nyt, mitä tapahtuu, kun t = 10 minuutin aika ylitetään: voi tapahtua, että ylimääräinen on kokonaisluku, esimerkiksi, että keskustelu kestää tarkalleen 11, 12, 13, 14 minuuttia tai enemmän. Siinä tapauksessa puhelun määrä on:

f (t) = 0.40 + 0.05 (T-10) $, T: n yli 10 minuuttia, kokonaisella T: llä.

Toisin sanoen tässä tapauksessa: t = 11, 12, 13, 14, 15 ... minuuttia.

Oletetaan esimerkiksi, että keskustelu kestää tarkalleen 15 minuuttia, kustannukset ovat:

f (15) = 0.40 + 0.05 (15-10) $ = 0.65 dollaria

Desimaalitapaus

Lopuksi harkitse tapausta, jossa puhelu kestää jonkin aikaa desimaaliosalla. Oletetaan esimerkiksi, että puhelu kestää 15 minuuttia ja 45 sekuntia, mikä olisi desimaalisesti 15.75 minuuttia.

Voimme ilmaista sen koko lattiatyypin osana olettaen, että yritys haluaa antaa enemmän etuja asiakkaalle tai taivaalle:

f (t) = 0.40 + 0.05 ⋅ [[T-9]] $

Katsotaanpa mitä asiakas maksaa, jos se olisi lattiatoiminto:

F (15.75) = 0.40 + 0.05 ⋅ [[15.75-9]] $ = 0.40 + 0.05⋅ [[6.75]] $ = 0.40 + 0.05 × 6 $ = 0.70 dollaria.

Tai taivaan funktiona, siinä tapauksessa kustannukset olisivat:

F (15.75) = 0.40 + 0.05 [[15.75-9]] $ = 0.40 + 0.05⋅ [[6.75]] $ = 0.40 + 0.05 × 7 $ = 0.75 $.

Toiminto ja graafinen

Osien määrittelemana funktiona on:

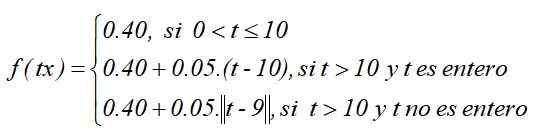
Funktion kaavio olisi tällainen, olettaen, että koko kattotyyppi on valittu:

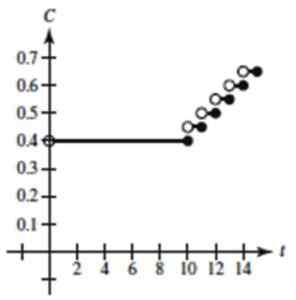Kuva 4. Harjoituksen askelfunktion kaavio ratkaistu 1. Lähde: Larson, R. Muuttujan laskenta.

- Harjoitus 2

Laske integraali ∫S (x) DX välillä -3 ja 3 askelfunktion välillä:

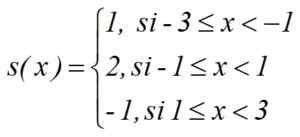
Ratkaisu

Käytämme määritelmää porrastetun toiminnon integraaliin:

Siksi integraali on: I:

I = 1. [(-1)-(-3)] + 2.[1- (-1)]+(-1).[3-1] = 2+4-2 = 4

Viitteet

1. Jiménez, r. 2006.Matemaattiset toiminnot. Pearson -koulutus.
2. Larson, r. 2010. Muuttujan laskenta. 9NA. Painos. McGraw Hill.
3. Matematiikka IV. Funktiot. Toipunut: Cobaqroo.Edu.MX.
4. Wikipedia. Koko osatoiminnot. Palautettu: on.Wikipedia.org.
5. Wikipedia. Porrastettu toiminta. Palautettu: on.Wikipedia.org.