Eksponentiaaliset funktioominaisuudet, esimerkit, harjoitukset

Se eksponentti funktio Se on erittäin tärkeä matemaattinen tehtävä monille sovelluksille, joita sillä on. Se on määritelty seuraavasti:

f (x) = b^x, B> 0: n ja b ≠ 1: n kanssa

Missä B on todellinen vakio aina positiivinen ja erilainen kuin 1, joka tunnetaan nimellä pohja. Huomaa, että todellinen muuttuja x löytyy eksponentti, Tällä tavalla f (x) on aina todellinen luku.

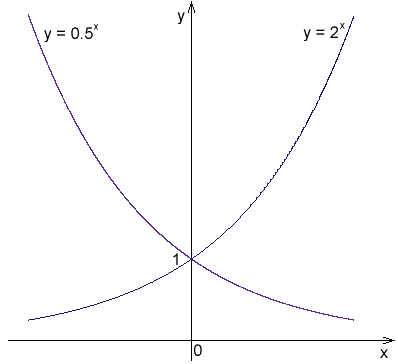Kuvio 1. Eksponentiaaliset toiminnot, joissa on 2 ja 1/2

Esimerkkejä eksponentiaalisista toiminnoista ovat seuraavat:

-f (x) = 2^x

-g (x) = 5⋅e^-3x

-H (x) = 4⋅ (10^2x-A

Nämä ovat toimintoja, jotka kasvavat - tai vähenevät eksponentin merkin mukaan - erittäin nopeasti, joten puhuu "eksponentiaalisesta kasvusta", kun jokin voimakkuus kasvaa hyvin nopeasti. Siksi he ovat tarkoituksenmukaisia ​​mallintaa elävien olentojen kasvua, kuten bakteereja.

Toinen erittäin mielenkiintoinen sovellus on yhdistelmäkorko. Mitä enemmän rahaa sinulla on tilillä, sitä enemmän etuja ja he voivat laskea jokaisen tietyn ajanjakson, niin pieni kuin haluat.

Logaritmisen funktion avulla, joka on eksponentiaalin käänteinen tehtävä, se voidaan tietää, kuinka kauan tietty pääoma kasvaa tiettyyn arvoon.

[TOC]

Eksponentiaaliset funktioominaisuudet

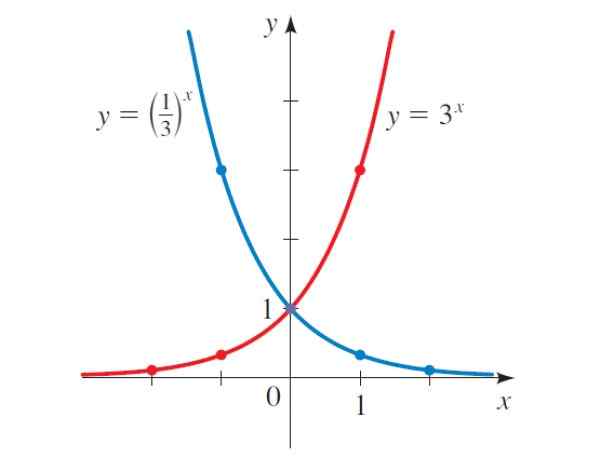
Kuva 2. Esimerkkejä eksponentiaalisista toiminnoista. Lähde: f. Zapata.

Seuraavat ovat minkä tahansa eksponentiaalisen funktion yleiset ominaisuudet:

-Minkä tahansa eksponentiaalisen funktion kaavio leikkaa aina pystysuuntaisen akselin pisteessä (0,1), kuten kuvassa 2 voidaan nähdä. Tämä johtuu siitä, että b^{0 -} = 1 kaikille B -arvoille.

-Eksponentiaalinen funktio ei leikkaa X -akselia, itse asiassa tämä akseli on funktion vaakasuora asymptootti.

-Koska b¹ = b, kohta (1, b) kuuluu aina funktiografiikkaan.

Se voi palvella sinua: hepagonaalinen prisma

-Eksponentiaalisen funktion alue on reaalilukujen joukko ja f (x) = b^x Se on jatkuvaa kaikella alueella.

-Eksponentiaalisen funktion alue on kaikki suurempi kuin 0, mikä havaitaan myös grafiikalla.

-Eksponentiaalinen funktio on yksi kerrallaan, ts. Jokaisella funktion alueelle kuuluvalle X -arvolle on ainutlaatuinen kuva saapumisjoukossa.

-Eksponentiaalisen käänteinen on logaritminen funktio.

Eksponentiaalisen funktion erityiset ominaisuudet

Kuten olemme aiemmin sanoneet, eksponentiaalinen funktio voi kasvaa tai vähentää.

Jos kuvan 2 kuvaajaa tutkitaan huolellisesti, on huomattava, että jos b> 1, funktio kasvaa, esimerkiksi y = 3^x, Mutta y = (1/3) tapauksessa^x, b: n kanssa < 1, la función decrece.

Meillä on kahden tyyppisiä eksponentiaalisia funktioita seuraavilla erityisillä ominaisuuksilla:

B> 1

-Toiminto kasvaa aina.

-Kun B: n arvo kasvaa, funktio kasvaa nopeammin, esimerkiksi y = 10^x kasvaa nopeammin kuin y = 2^x.

-Kun muuttuja on suurempi kuin 0, funktio saa arvot suuremmat kuin 1, eli:

X> 0: y> 1

-Ja jos x<0, entonces f(x) < 1.

B: lle < 1

-Funktio vähenee aina.

-Laskemalla B: n arvoa, funktio vähenee vielä nopeammin. Esimerkiksi y = (1/5)^x vähenee nopeammin kuin y = (1/3)^x.

-Arvoille x pienempi kuin 0, funktio vie yli 1 arvot, ts

X 1

-Lopuksi, kun x> 0, sitten ja < 1.

Esimerkkejä eksponentiaalisista toiminnoista

Eksponentiaalinen funktio on erittäin hyödyllinen tieteen ja talouden ilmiöiden mallintamisessa, kuten alla näemme:

Luonnollinen eksponentiaalinen funktio

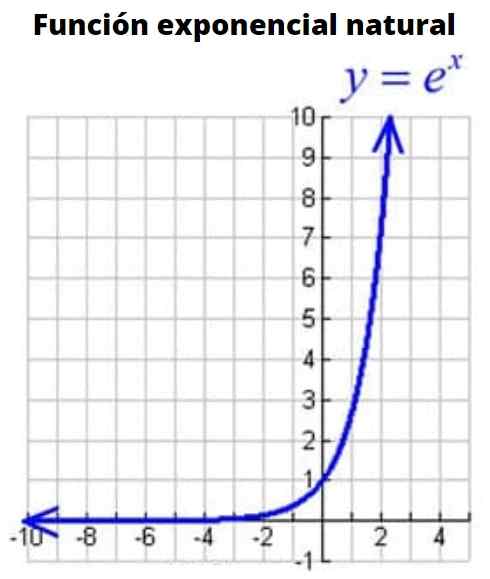Kuva 3: Luonnollinen eksponentiaalinen funktiokaavio

Se on funktio, jonka kanta on numero E- tai Euler -numero, irrationaalinen numero, jonka arvo on:

Voi palvella sinua: Lisäkulmat: Mitä ovat, laskenta, esimerkit, harjoitukset

E = 2.718181828…

Tämä pohja, vaikka se ei olisikaan pyöreä numero, toimii erittäin hyvin lukuisiin sovelluksiin. Siksi sitä pidetään kaikkien eksponentiaalisten toimintojen tärkeimpänä perustana. Luonnollinen eksponentiaalinen funktio ilmaistaan ​​matemaattisella tavalla seuraavasti:

f (x) = e^x

Eksponentiaalinen funktio esiintyy usein todennäköisyydessä ja tilastoissa, koska erilaiset todennäköisyysjakaumat, kuten normaali jakauma, Poisson ja muut, voidaan ilmaista eksponentiaalisten funktioiden avulla.

Jatkuva yhdistelmäkohde

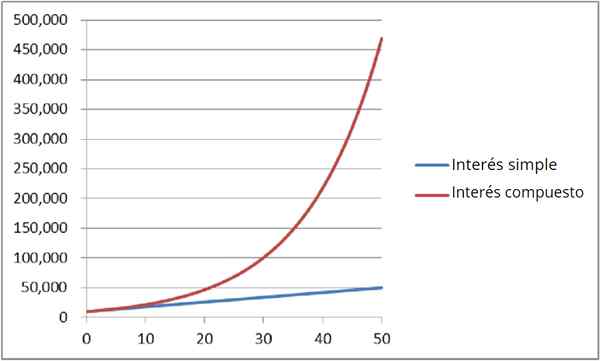Kuva 4: Yksinkertaisen ja yhdisteen kiinnostuksen vertailu

Sitä kutsutaan myös Jatkuva isku. Tietää rahan määrä -Lla Sinulla on jälkeen t Vuotta käytetään eksponentiaalista ilmaisua:

A (t) = p ⋅ e^Rt

Jos p on alun perin talletettu rahan määrä, r on korko vuodessa ja lopulta t on vuosien lukumäärä.

Bakteerien kasvu

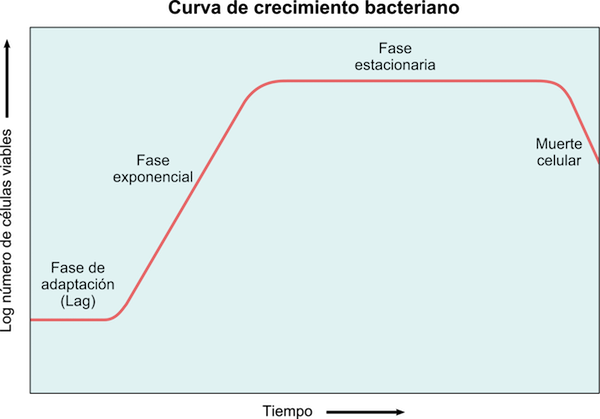Kuva 5: Bakteerien kasvukäyrä, jossa havaitaan latenssi, eksponentiaalinen, paikallaan oleva ja kuoleman vaiheet

Bakteerit kasvavat eksponentiaalisesti, joten kasvua voidaan mallintaa:

N (t) = n_jompikumpi ⋅ e ^Kt

Missä n (t) on nykyinen väestö ajan jälkeen (melkein aina tunteja), n_jompikumpi Alkupopulaatio ja k on vakio, joka riippuu bakteerityypistä ja olosuhteista, joissa käytettävissä olevat ravintoaineet.

Radioaktiivinen rappeutuminen

Tietyt luonnon ytimet ovat epävakaita, joten ne kieltäytyvät muuttuvan vakaammiksi, prosessi, joka voi olla hyvin lyhyt tai ottaa tuhansia vuosia isotoopista riippuen. Radioaktiivisten rappeutumishiukkasten aikana säteilee ja joskus myös fotoneja.

Joillakin radioaktiivisilla isotooppeilla on lääketieteellisiä sovelluksia, esimerkiksi radioaktiivinen jodi I-131, jota lääkärit käyttävät tiettyjen kilpirauhanen diagnosointiin ja hoitoon.

Radioaktiivinen rappeutuminen on mallinnettu eksponentiaalisella toiminnolla.

Voi palvella sinua: kuinka monta kymmenesosaa on yksikössä?

Ratkaisut

Yhtälöitä, joissa tuntematon esiintyy eksponenttina, kutsutaan eksponentiaaliseksi yhtälöksi. Tuntemattoman arvon tyhjentämiseksi käytetään erilaisia ​​algebrallisia manipulaatioita ja logaritmifunktion käyttöä, joka on eksponentiaalisen käänteinen funktio.

Katsotaanpa joitain ratkaistuja harjoituksia, jotka kuvaavat asiaa.

- Harjoitus 1

Ratkaise seuraavat eksponentiaaliset yhtälöt:

5^x = 625

b) 5^x = 2^X-1

Liittää jhk

Numero 625 on viiden moninkertainen, käytännössä, kun hajotetaan, havaitsemme sen:

625 = 5⁴

Siksi voimme kirjoittaa:

5^x = 5⁴

Koska tukikohdat ovat yhtä suuret kuin vasen että oikea, voimme sovittaa eksponentit ja saada:

x = 4

Ratkaisu b

Tätä harjoitusta varten emme voi turvautua aiemmin käytettyyn tekniikkaan, koska emäkset eivät ole samoja. Mutta voimme soveltaa logaritmia tasa -arvon molemmille puolille tällä tavalla:

5^x = 2^X-1

Loki (5^x) = loki (2^X-1-A

Nyt sovelletaan seuraavaa logaritmien omaisuutta:

Loki mⁿ = n⋅log m

Ja pysyy:

x⋅log 5 = (x-1) ⋅log 2

x⋅ (log 5 - log 2) = -log 2

x = - log 2 ÷ (log 5 - log 2)

- Harjoitus 2

Osoita, mitä funktiota jokainen alla esitetyt kaaviot vastaavat:

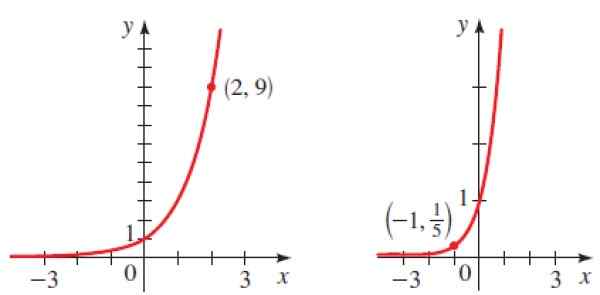Kuva 6. Grafiikka parast Ratkaisun harjoituksen 2 eksponentiaaliset toiminnot. Lähde: Stewart. J -. Ennakkoluulo.

Liittää jhk

Koska se on kasvava kuvaaja, B on suurempi kuin 1 ja tiedämme, että kohta (2.9) kuuluu kaavioon, siksi:

y = b^x → 9 = b²

Tiedämme, että 3² = 9, siksi b = 3 ja funktio on y = 3^x

Ratkaisu b

Korvaamme jälleen annetun pisteen (-1, 1/5) y = b^x saada:

1/5 = b^-1 = 1/b

Sitten b = 5 ja haluttu toiminto on:

y = 5^x

Viitteet

1. Figuera, J. 2000. 1. matematiikka. Monipuolinen. Co-bo-painikkeet.
2. Gid Hoffmann, J. Matematiikkakysymysten valinta 4. Vuosi. Ed. Spphinx.
3. Jiménez, r. 2008. Algebra. Prentice Hall.
4. Larson, r. 2010. Muuttujan laskenta. 9NA. Painos. McGraw Hill.
5. Stewart, J. 2006. Precculment: Laskentamatematiikka. Viides. Painos. Cengage -oppiminen.