Homografinen funktio kuinka kuvaaja, ratkaisut harjoitukset

Se funktioHomografinen tai rationaalinen Ón Se on eräänlainen matemaattinen funktio, joka koostuu kahden polynomikomponentin jakautumisesta. Se tottelee muotoa p (x)/q (x), missä q (x) ei voi olla nollamuotoa.

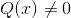
Esimerkiksi lauseke (2x - 1)/(x + 3) vastaa homografista funktiota p (x) = 2x - 1 y q (x) = x + 3.

Lähde: Pixabay.com

Homografiset toiminnot muodostavat analyyttisten toimintojen tutkimusosan, jota käsitellä. Tämä johtuu rajoituksista ja säätiöistä, joita on sovellettava niiden päätöslauselmiin.

[TOC]

Mikä on homografinen funktio?

Ne ovat ainutlaatuisen muuttujan rationaalisia lausekkeita, vaikka tämä ei tarkoita, että kahdelle tai useammalle muuttujalle ei ole samanlaista ilmaisua, missä se olisi jo avaruuksien kehon läsnäollessa, jotka noudattavat samoja malleja kuin homografinen funktio tasolla tasolla.

Niillä on joissain tapauksissa todellisia juuria, mutta pystysuorien ja vaakasuorien asymptoottien olemassaolo ylläpidetään aina, samoin kuin myös kasvu- ja vähentymisvälien väliajoja. Yleensä vain yksi näistä suuntauksista on läsnä, mutta on olemassa ilmaisuja, jotka kykenevät osoittamaan molemmat kehityksessä.

Hänen verkkotunnustaan ​​rajoittavat nimittäjän juuret, koska todellisten lukujen nollan välillä ei ole jakautumista.

Sekoitettu homografinen toiminta

Ne ovat hyvin usein laskelmassa, erityisesti differentiaalisia ja kattavia, jotka ovat välttämättömiä tietyissä kaavoissa ja anti -anti -anti -anti -. Jotkut yleisimmistä luokitellaan alla.

N. Homografisen toiminnon pari

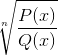
Sulkee pois kaikki alueen elementit, jotka tekevät argumentin negatiivisesta. Jokaisessa polynomissa olevat juuret osoittavat nolla -arvoja arvioidessaan.

Radikaali hyväksyy nämä arvot, vaikka homografisen toiminnan perustavanlaatuista rajoitusta olisi otettava huomioon. Missä Q (x) ei voi vastaanottaa nolliarvoja.

Voi palvella sinua: Transsendenttiset toiminnot: Tyypit, määritelmä, ominaisuudet, esimerkit

Väliajojen ratkaisut on siedettävä:

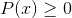
Risteyksien saavuttamiseksi merkkimenetelmää voidaan käyttää muun muassa.

Homografinen funktio logaritmi

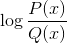
Sulkee pois verkkotunnusarvot, jotka heittävät negatiiviset välit ja nollat. Koska nollat ​​on jo suljettu nimittäjästä, ratkaisut: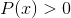

On myös yleistä löytää molemmat lausekkeet yhdessä, muun muassa mahdollisissa yhdistelmissä.

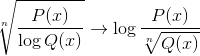
Kuinka graafoida homografinen toiminto?

Homografiset funktiot vastaavat graafisesti hyperbolien kanssa tasossa. Jotka kuljetetaan vaakasuoraan ja pystysuoraan polynomit määrittelevien arvojen mukaan.

On olemassa useita elementtejä, jotka meidän on määriteltävä rationaalisen tai homografisen toiminnon piirtämiseksi.

Omaisuus

Ensimmäinen on funktioiden p ja q juuret tai nollat.

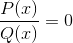
Saavutetut arvot merkitään grafiikan X -akselilla. Kaavion leikkauspisteet akselin kanssa.

Pystysuuntainen asymptootti

Vastaa pystysuuntaisia ​​viivoja, jotka purkaavat kuvaajan niiden esittämien suuntausten mukaan. Ne koskettavat X -akselia arvoissa, jotka tekevät nimittäjästä nollan, eikä homografisen funktion kuvaaja koskaan kosketa niitä.

Vaakasuuntainen asymptootti

Vaakasuuntaisen ompeleen viivalla on rajattu raja, jolle funktiota ei määritetä tarkkaan kohtaan. Trendejä havaitaan ennen tätä linjaa ja sen jälkeen.

Sen laskemiseksi meidän on turvauduttava menetelmään, joka on samanlainen kuin L'hopital -menetelmä, jota käytetään rationaalisten funktioiden rajojen ratkaisemiseen, joilla on taipumus äärettömyyteen. Numeraattorin korkeimman voiman kertoimet ja funktion nimittäjä on otettava.

Esimerkiksi seuraavalla lausekkeella on vaakasuora asymptootti y = 2/1 = 2.

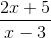
Kasvuväli

Tilattujen arvojen arvot ovat merkitty kuvaajaan asymptoottien takia. Kasvun tapauksessa funktio kasvaa arvoista, kun verkkotunnuksen elementit vasemmalta oikealle arvioidaan.

Voi palvella sinua: 60 jakajaa

Vähenevä aikaväli

Tilatut arvot vähenevät, kun verkkotunnuksen elementit vasemmalta oikealle arvioidaan.

Arvoista löytyviä hyppyjä ei oteta huomioon kasvaessa tai vähentyessä. Tämä tapahtuu, kun kuvaaja on lähellä pystysuoraa tai horisonttia.

Risteys y: n kanssa

Nollaa x x: n arvo on risteys Ordinaattien akselin kanssa. Tämä on erittäin hyödyllinen tosiasia rationaalisen funktion kaavion saamiseksi.

Esimerkit

Määritä seuraavien lausekkeiden kaavio, löydä sen juuret, pystysuorat ja vaakasuorat asymptotit, kasvu- ja vähentymisvälien ja risteyksen tilatun akselin kanssa.

Harjoitus 1

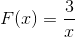
Lausekkeesta puuttuu juuret, koska sillä on vakio arvo osoittajalla. Rajoitus sovelletaan x erilainen kuin nolla. Vaakasuuntaisella asymptotilla y = 0: ssa ja asymptootin pystysuorassa x = 0. Akselin kanssa ei ole risteyspisteitä ja.

Havaitaan, että kasvuvälejä ei ole edes hyppäämällä vähemmän äärettömemmäksi x = 0.

Laskuväli on

Id: (-∞; o) u (0, ∞)

Harjoitus 1.2

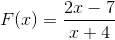
2 polynomia havaitaan kuten alkuperäisessä määritelmässä, joten jatkamme vakiintuneiden vaiheiden mukaisesti.

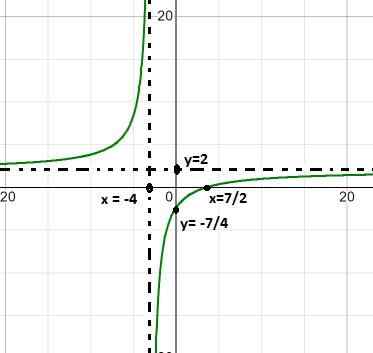
Löydetty juuri on x = 7/2, joka johtuu funktion tasaamisesta.

Pystysuuntainen asymptootti on x = - 4, joka on aluetta jätetty arvo rationaalisen funktio -olosuhteen vuoksi.

Vaaka -asymptootti on y = 2: ssa, tämän jakamisen jälkeen 2/1, luokan 1 muuttujien kertoimet.

Sillä on risteys y = - 7/4. Arvo, joka löytyy x: n tasaamisen jälkeen nollaan.

Se voi palvella sinua: fraktio vastaa 3/5 (ratkaisu ja selitys)

Toiminto kasvaa jatkuvasti, hyppäämällä enemmän vähemmän äärettömään juuren X = -4 ympärillä.

Sen kasvuväli on ( -∞, - 4) u ( - 4, ∞).

Kun x: n arvo on lähellä vähemmän ääretöntä, funktio vie arvot lähellä 2. Sama tapahtuu, kun X lähestyy ääretöntä.

Ekspressio lähestyy äärettömämpää, kun arvioidaan - 4 vasemmalla ja vähemmän ääretön, kun sitä arvioidaan - 4 oikealla puolella.

Harjoitus 2

Seuraavan homografisen funktion kuvaaja havaitaan:

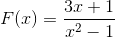
Kuvaile heidän käyttäytymisensä, juuret, pystysuuntaiset ja vaakasuorat asymptotit, kasvu- ja vähentymisvälien sekä risteyksen tilatun akselin kanssa.

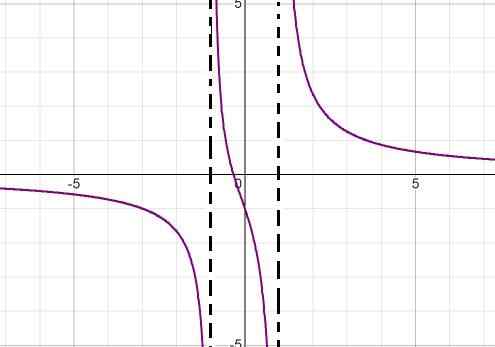
Lausekkeen nimittäjä osoittaa ottamalla huomioon neliöiden ero (x + 1) (x - 1) juurten arvot. Tällä tavalla molemmat pystysuorat asymptotit voidaan määritellä seuraavasti:

x = -1 ja x = 1

Vaaka -asymptootti vastaa abskissan akselia, koska tärkein voima on nimittäjässä.

Sen ainoa juuri on määritelty x = -1/3.

Lauseke pienenee aina vasemmalta oikealle. Se lähestyy nollaa, kun sillä on taipumus äärettömyyteen. Vähemmän äärettömästi lähestyessäsi -1 vasemmalla. Ääretön lähestyessäsi -1 oikealla. Vähemmän ääretön lähestyessäsi yhtä vasemmalla ja enemmän äärettömyyttä lähestyessäsi yhtä oikealla.

Viitteet

1. Likiarvo rationaalisilla funktioilla. Donald J. Uusi mies. Amerikan matemaattinen yhteiskunna., 31. joulukuuta. 1979
2. Ortogonaalinen luokitustoiminnot. La Laguna -yliopiston tenerife Adhemar Bultheel, Adhemar Bultheel, Pablo Gonzalez-Vera, Erik Hendriksen, Olav NJSTAD. Cambridge University Press, 13. helmikuuta. 1999
3. Real -toimintojen arviointi. P. P. Petrushev, Vasil Atanasov Popov. Cambridge University Press, 3. maaliskuuta. 2011
4. Algebralliset toiminnot. Gilbert Ames Bliss. Couer Corporation, 1. tammikuuta. 2004
5. Espanjan matemaattinen yhdistyksen aikakauslehti, 5-6 osaa. Espanjan matemaattinen yhdistys, Madrid 1916