Transsendenttiset funktiotyypit, määritelmä, ominaisuudet, esimerkit

Se Transsendenttitoiminnot Elementt. Toisin sanoen ne ovat niitä, joita ei voida ilmaista polynomilla, polynomi- tai polynomijuurisuhteella. 

Elementsittömät transcendent-toiminnot tunnetaan myös nimellä erityistoiminnot, ja niiden joukossa virhetoiminto voidaan nimetä. Se algebralliset toiminnot (Polynomit, polynomiajattelut ja polynomijuuret) vieressä Transsendenttitoiminnot Elementalit muodostavat sen, mitä matematiikassa tunnetaan nimellä Alkeisfunktiot.

Sitä pidetään myös transcendenttisia toimintoja, jotka johtuvat transsendenttien toimintojen välillä tai transcendenttien ja algebrallisten funktioiden välillä. Nämä toiminnot ovat: toimintojen summa ja ero, funktioiden tuote ja suhde sekä kahden tai useamman toiminnon koostumus.

[TOC]

Määritelmä ja ominaisuudet

Eksponentti funktio

Se on muodon todellisen riippumattoman muuttujan todellinen funktio:

f (x) = a^x = a^x

missä -lla Se on positiivinen reaaliluku (A> 0) kiinteä nimeltään pohja. Ympyrän tai valvontaa käytetään määrityksen merkitsemiseen.

Laitetaan tapaukseen A = 2 Sitten funktio on näin:

f (x) = 2^x = 2^x

Joka arvioidaan riippumattoman muuttujan x useille arvoille:

Alla on grafiikka, jossa esitetään useiden perusarvojen eksponentiaalinen funktio, mukaan lukien emäs ja (Neper -numero ja ≃ 2.72). Pohja ja On niin tärkeää, että yleensä puhut eksponentiaalisesta toiminnasta E^x, Se on myös merkitty exp (x).

Kuvio 1. Eksponentiaalinen funktio A^x, useille pohja -arvoille A. (Oma yksityiskohta)

Eksponentiaaliset funktioominaisuudet

Kuviosta 1 voidaan nähdä, että eksponentiaalisten funktioiden alue on reaalilukuja (DOM F = R -) ja alue tai reitti ovat positiivisia todellisia (Ran f = R -⁺-A. 

Voi palvella sinua: Symmetria

Toisaalta, riippumatta pohjan A arvosta, kaikki eksponentiaaliset toiminnot kulkevat pisteen (0, 1) ja pisteellä (1, a) läpi. 

Kun pohja A> 1, Sitten funktio kasvaa ja milloin 0 - < a < 1 Funktio pienenee. 

Käyrät y = a^x ja y = (1/a)^x  Ne ovat symmetrisiä akselin suhteen JA. 

Lukuun ottamatta tapausta A = 1, Eksponentiaalinen funktio on injektio, ts. Kuvan jokaiseen arvoon yksi vastaa ja vain lähtöarvo.

Logaritminen funktio

Se on todellisen riippumattoman muuttujan todellinen todellinen funktio, joka perustuu numeron logaritmin määritelmään. Logaritmipohjainen -lla lukumäärä x, Se on numero ja johon perus on nostettava argumentin saamiseksi x-

Hirsi_-lla(x) = y ⇔ a^y = x

Tuo on logaritmitoiminto pohjassa -lla Se on käänteinen funktio eksponentiaaliseen funktioon perustuen -lla.

Esimerkiksi:

Hirsi₂1 = 0, koska 2^0 = 1

Toinen tapaus, loki₂4 = 2, koska 2^2 = 4

2: n juuren logaritmi on loki₂√2 = ½, koska 2^½ = √2

Hirsi₂ ¼ = -2, katsoen 2^(-2) = ¼ 

Alla on kaavio logaritmifunktiosta eri emäksissä.

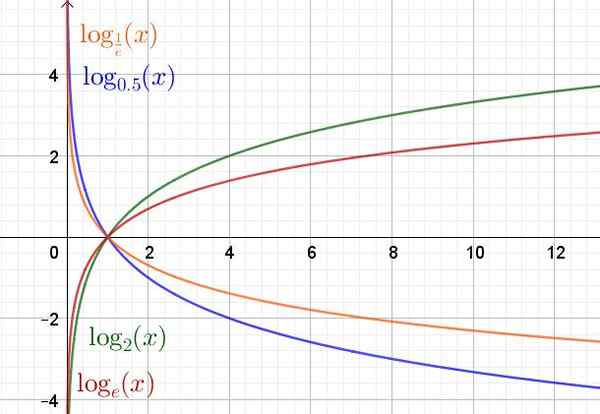Kuva 2. Eksponentiaalinen funktio eri perusarvoille. (Oma yksityiskohta)

Logaritmo -toimintoominaisuudet

Logaritmifunktion verkkotunnus ja (x) = loki-lla(x)  Ne ovat positiivisia todellisia lukuja R -+. Alue tai reitti ovat todellisia numeroita R -.

Perustasta riippumatta logaritmifunktio kulkee aina pisteen (1.0) ja piste (A, 1) kuuluu mainitun funktion kuvaajaan.

Se voi palvella sinua: jonoteoria: historia, malli, mihin se on ja esimerkkejä

Siinä tapauksessa, että emäs A on suurempi kuin yksikkö (A> 1), logaritmifunktio kasvaa. Mutta kyllä ​​(0 < a < 1) entonces es una función decreciente.

Seno-, Coseno- ja tangenttitoiminnot

Sine -funktio antaa todellisen numeron ja jokaiselle arvolle x, missä x edustaa radianien kulman mittausta. SEN (x) -arvon saamiseksi kulmasta, kulma on esitetty yksikköympyrässä ja mainitun kulman projektio pystysuoralla akselilla on rintoja, jotka vastaavat tätä kulmaa.

Alla on (kuvassa 3) trigonometrinen ympyrä ja rinta useille kulma -arvoille x1, x2, x3 ja x4.

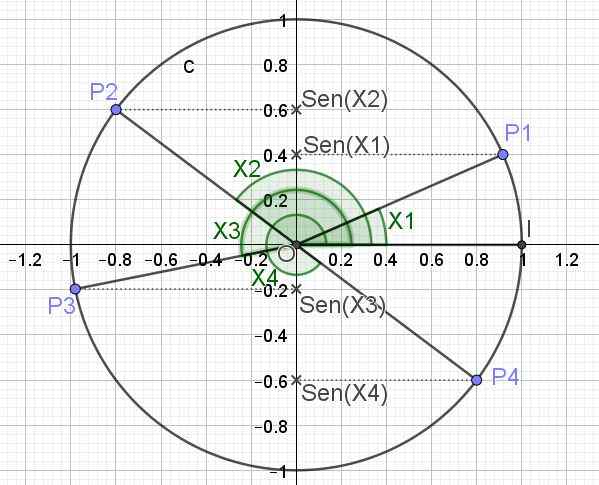Kuva 3. Trigonometrinen ympyrä ja useiden näkökulmien rinta. (Oma yksityiskohta)

Tällä tavoin määritelty maksimiarvo, jolla Sen (x) -funktio voi olla, on 1, joka tapahtuu, kun x = π/2 + 2π n on kokonaisluku (0, ± 1, ± 2,). Minimiarvo, jonka Sen (x) -toiminto voi kestää, kun x = 3π/2 + 2π n. 

Coseno y = cos (x) -funktio määritetään samalla tavalla, mutta kulma -asentojen P1, P2 jne. Projektio suoritetaan trigonometrisen ympyrän vaaka -akselilla.

Toisaalta y = tan (x) -funktio on sinifunktion ja kosinifunktion välinen suhde.

Sitten esitetään kaavio transcendent -funktioista sen (x), cos (x) ja tan (x)

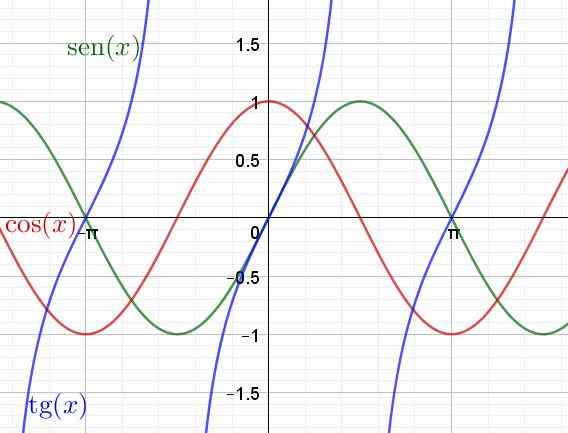Kuva 4. Transsendenttien funktioiden, rinnan, kosinin ja tangentin kaavio. (Oma yksityiskohta)

Ja olennainen

Johdettu eksponentiaalisesta toiminnasta

Johdannainen ja' eksponentiaalisesta toiminnasta y = a^x Se on funktio a^x kerrottuna hänestä Pohjan a neperian logaritmi a-

Voi palvella sinua: Aseta teoria: Ominaisuudet, elementit, esimerkit, harjoitukset

ja '= (a^x)' = a^x ln a

Erityistapauksessa ja, Eksponentiaalisen funktion johdannainen on itse eksponentiaalinen funktio.

Eksponentiaalisen toiminnon olennainen

Määrittelemätön integraali a^x Se on funktio jaettuna pohjan Neperian logaritmin kesken. 

Base E: n erityistapauksessa eksponentiaalisen funktion integraali on itse eksponentiaalinen funktio.

Transsendenttisten funktioiden johdannainen ja integraali taulukko

Alla on yhteenveto taulukko tärkeimmistä transcendent -toiminnoista, sen johdannaisista ja määrittelemättömistä (antiDervantive):

Joidenkin transsendenttien funktioiden määrittelemätön johdannainen ja integraali taulukko. (Oma yksityiskohta)

Esimerkit

Esimerkki 1

Etsi funktion f (x) = x^3 koostumuksen tuloksena oleva funktio funktiolla g (x) = cos (x):

(f tai g) (x) = f (g (x)) = cos³(x)

Sen johdannainen ja sen määrittelemätön integraali on:

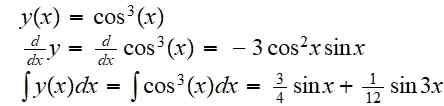
Esimerkki 2

Löydä G -funktion koostumus F -funktioon, koska olet G ja F edellisessä esimerkissä määriteltyjä toimintoja:

(g tai f) (x) = g (f (x)) = cos (x³-A

On huomattava, että toimintojen koostumus ei ole kommutatiivinen operaatio.

Johdannainen ja määrittelemätön integraali tälle funktiolle ovat vastaavasti:

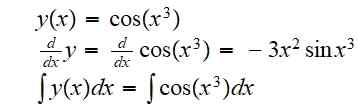
Integraali jätettiin ilmoitettuna, koska tulosta ei ole mahdollista kirjoittaa elementtifunktioiden yhdistelmänä tarkalla tavalla.

Viitteet

1. Yhden muuttujan laskenta. Ron Larson, Bruce H. Edwards. Cengage Learning, 10. marraskuuta. 2008
2. Implisiittinen funktion lause: historia, teoria ja sovellukset. Steven G. Krantz, Harold R. Puistot. Springer Science & Business Media, 9. marraskuuta. 2012
3. Monimuuttuja -analyysi. Sable Shirali, Harkrishan Lal Vasudeva. Springer Science & Business Media, 13. joulukuuta. 2010
4. Järjestelmän dynamiikka: Mechatronic -järjestelmien mallintaminen, simulointi ja hallinta. Dekaani C. Karnopp, Donald L. Margolis, Ronald C. Rosenberg. John Wiley & Sons, 7. maaliskuuta. 2012
5. Laskenta: Matematiikka ja mallinnus. William Bauldry, Joseph R. Fiedler, Frank R.Giordano, Ed Lodi, Rick Vitray. Addison Wesley Longman, 1. tammikuuta. 1999
6. Wikipedia. Transsendentti -funktio. Palautettu: on.Wikipedia.com