Heptadecágono -ominaisuudet, diagonaalit, kehä, alue

Hän heptadecágono Se on säännöllinen monikulmio, jossa on 17 sivua ja 17 kärkeä. Sen rakenne voidaan tehdä euklidian tyyliin, toisin sanoen vain sääntöä ja kompassia käyttämällä. Se oli matematiikan suuri nero Carl Friedrich Gauss (1777-1855), joka laski vain 18-vuotiaat, jotka löysivät sen rakennusmenettelyn vuonna 1796. 

Ilmeisesti Gauss tunsi olevansa aina erittäin taipuvainen tähän geometriseen hahmoon siihen pisteeseen, että siitä päivästä lähtien, kun hän löysi rakenteensa, hän päätti olla matemaatikko. Sanotaan myös, että hän halusi,.

Kuvio 1. Heptadecágono on säännöllinen monikulmio, jossa on 17 puolta ja 17 kärkipistettä. Lähde: f. Zapata.

Gauss löysi myös kaavan sen määrittämiseksi, mitkä tavalliset monikulmiot ovat mahdollisuuden rakentaa sääntöllä ja kompassilla, koska joillakin ei ole tarkkaa euklidista rakennetta.

[TOC]

Heptadecágonon ominaisuudet

Mitään ominaisuuksiaan, kuten jokainen monikulmio, sen sisäkulmien summa on tärkeä. Tavallisessa monikulmiossa n Sivut, summa annetaan:

SA (n) = (n -2) *180º.

Heptadecágonolle puolten lukumäärä n On 17, Mikä tarkoittaa, että sen sisäkulmien summa on:

SA (17) = (17 - 2) * 180º = 15 * 180º = 2700º.

Tämä summa, Radianesissa ilmaistuna, on tällainen:

SA (17) = (17 - 2) * π = 15 * π = 15π

Edellisistä kaavoista voidaan helposti päätellä, että heptadecágonon jokaisella sisäkulmalla on tarkka a -mittaus:

α = 2700º/17 = (15/17) π radianit

Tästä seuraa, että sisäinen kulma on suunnilleen:

α ≈ 158 824º

Diagonaalit ja kehä

Diagonaali ja kehä ovat muita tärkeitä näkökohtia. Missä tahansa monikulmiossa diagonaalien lukumäärä on: 

D = n (n - 3) / 2 ja heptadecágonon tapauksessa, kuten N = 17, Sinun täytyy D = 119 diagonaalit.

Voi palvella sinua: Trinomial

Toisaalta, jos heptadecágonon kummankin puolen pituus tunnetaan, tavallisen Heptadecágonin kehä lisää yksinkertaisesti 17 kertaa tämän pituuden tai mikä on vastaava 17 kertaa pituus d -d Kummallakin puolella:

P = 17 d

Heptadecágonon kehä 

Joskus vain radio tunnetaan r - heptadecágonosta, joten on välttämätöntä kehittää kaava tälle tapaukselle.

Tätä varten käsite apoteemi. Apotheem on segmentti, joka menee tavallisen monikulmion keskustasta toisella puolella olevaan keskipisteeseen. Apotemi suhteessa sivuun on kohtisuorassa kyseiselle puolelle (katso kuva 2).

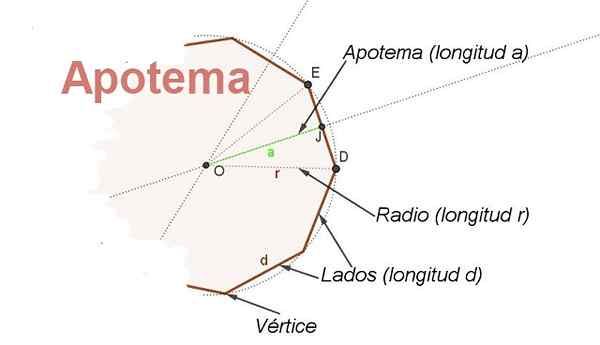Kuva 2. Säännöllisen radion R -monikulmion ja sen apoteemin osat on esitetty. (Oma yksityiskohta)

Lisäksi apoteemi on kulman puolustaja, jossa on keskimmäinen kärki ja polygonin kahdessa peräkkäisessä kärkipisteessä, tämä mahdollistaa radion välisen suhteen löytämisen r - ja puolella d -d.

Jos sitä kutsutaan β keskikulmaan Kyyppi Ja ottaen huomioon kyseisen apoteemin Oman on puolustaja Ex = d/2 = r Sen (β/2), missä sinulla on suhde löytääksesi pituuden d -d Monikulmion puolella tunsi radionsa r - ja sen keskuskulma β-

D = 2 r sin (β/2)

Heptadecágonin tapauksessa β = 360º/17 Mitä sinulla on:

D = 2 R Sen (180º/17) ≈ 0,3675 R

Lopuksi heptadecágonon kehän kaava, joka on saatu sen säteen saadaan:

P = 34 R Sen (180º/17) ≈ 6.2475 r

Heptadecágononin kehä PCIR = 2π r ≈ 6.2832 r.

Alue

Heptadecágonon alueen määrittämiseksi viitataan kuvaan 2, joka näyttää säännöllisen monikulmion sivut ja apoteemit n puolet. Siinä kuvassa kolmio EOD Sillä on pohja d -d (monikulmiopuoli) korkeudella -lla (Polygon -apoteemi) jaettuna 2-

Se voi palvella sinua: Virusarja: Esimerkkejä ja harjoituksia

Eod = (d x a) / 2

Joten tunnettu apotheme -lla heptadecágono ja sivu d -d Samasta on:

Heptadecágono -alue = (17/2) (d x a)

Pinta -ala

Saadaksesi kaavan Heptadecágonon alueelle, joka tietää sen seitsemäntoista sivun pituuden, on välttämätöntä saavuttaa suhde apotemin pituuden välillä -lla ja puolella d -d.

Kuvioon 2 viitaten sinulla on seuraava trigonometrinen suhde:

Tan (β/ 2) = esim./ Oj = (d/ 2)/ a, olemus β keskikulmaan Kyyppi. Niin tuo apotemi -lla voidaan laskea, jos pituus tunnetaan d -d monikulmiosta ja keskikulmasta β-

A = (d/2) cotan (β/2)

Jos tämä apoteemin lauseke korvataan nyt, edellisessä osassa saadun Heptadecágono -alueen kaavassa, sinulla on:

Heptadecágono -alue = (17/4) (D²) Cotan (β/2)

Olemus β = 360º/17 Heptadecágonolle, joten sinulla on vihdoin haluttu kaava:

Heptadecágono -alue = (17/4) (D²) Cotan (180º/17)

Radio -alue

Edellisissä osissa oli löydetty suhde tavallisen monikulmion ja sen R -radio r: n välisen suhteen, seuraava olento: Seuraava: Seuraava olento:

D = 2 r sin (β/2)

Tämä ilmaus d -d Se johdetaan alueen edellisessä osassa saatuun lausekkeeseen. Jos asiaankuuluvat substituutiot ja yksinkertaistukset tehdään, saadaan kaava, jonka avulla voidaan laskea Heptadecágono -alueen:

Heptadecágono -alue = (17/2) (R²) Sin (β) = (17/2) (R²) Sen (360º/17)

Alueen likimääräinen lauseke on:

Heptadecágono -alue = 3 0706 (R²-A 

Kuten odotettiin, tämä alue on hiukan vähemmän kuin heptadecágonille rajoitettu ympyrän alue -Lla_Kiertää = π r² ≈ 3 1416 r². Tarkemmin sanottuna se on 2% pienempi kuin sen rajoitetun ympyrän.

Voi palvella sinua: tavallisen ja epäsäännöllisen Pentagonin alue: miten se otetaan, harjoitukset

Esimerkit

Esimerkki 1

Jotta heptadecágonolla olisi 2 cm: n sivut, mikä arvo on rajoitetun kehän säteen ja halkaisijan tulisi olla? Löydä myös kehän arvo.

Kysymykseen vastaamiseksi on tarpeen muistaa N -sivujen säännöllisen monikulmion ja säteen välinen suhde:

 D = 2 R Sen (180º / N)

Heptadecágono N = 17, siten D = 0,3675 r, Toisin sanoen

Halkaisija 10 8844 cm.

2 cm: n puolen heptadecágonin kehä on p = 17* 2 cm = 34 cm.

Esimerkki 2

Paljon?

Edellisessä osassa on tarpeen viitata kaavaan, joka mahdollistaa heptadecágonon pinta -alan, kun pituus on d -d Hänen puolellaan:

Heptadecágono -alue = (17/4) (D²) / Tan (180º / 17) 

Vaihdettaessa D = 2 cm etukaavassa saadaan:

Alue = 90,94 cm

Viitteet

1. C. JA. -Lla. (2003). Geometriaelementit: harjoituksilla ja kompassin geometrialla. Medellinin yliopisto.
2. Campos, f., Cerecedo, f. J -. (2014). Matematiikka 2. Patria -toimitusryhmä.
3. Vapautettu, k. (2007). Tutustu monikulmioihin. Vertailuindeksiyhtiö.
4. Hendrik, V. (2013). Yleiset monikulmiot. Birkhäuser.
5. Iger. (S.F.-A. Matematiikka ensimmäisen lukukauden Tacaná. Iger.
6. Jr. Geometria. (2014). Monikulmio. Lulu Press, Inc.
7. Miller, Heeren ja Hornsby. (2006). Matematiikka: Perustelu ja sovellukset (kymmenes painos). Pearson -koulutus.
8. Patiño, m. (2006). Matematiikka 5. Toimitusohjelma.
9. Sada, m. Säännöllinen 17 puolta säännöllä ja kompassilla. Toipunut: Geogebra.org
10. Wikipedia. Heptadecágono. Palautettu: on.Wikipedia.com