Heptagoni

Esimerkki heptagonista

Mikä on heptagon?

Hän heptagoni Se on monikulmio, jolla on seitsemän puolta ja seitsemän sisäkulmaa. Geometrisena sanana sana heptagon on peräisin kreikasta Hepta, mikä tarkoittaa seitsemän ja gonot, käännettynä kulmana. Siksi se on monikulmio, jossa on seitsemän kulmaa.

Monikulmio on tasainen geometrinen luku, joka muodostaa ja sulkee kolme tai useampia segmenttejä, joita kutsutaan myös puolet. Yleisiä kohtia, joita sivuilla on Kärjet.

Vierekkäisten sivujen välinen alue, kuvan sisäpuolella, on Sisäkulma, jonka kärkipiste on myös yksi heptagonin kärjistä.

Jos kaikilla puolilla ja sisäkulmissa on sama mitta, se on a tavallinen heptagon, muuten on a epäsäännöllinen heptagon. Epäsäännölliset heptonit omaksuvat monenlaisia ​​muotoja.

Heptagon voi myös olla kupera jompikumpi kovera, sen sisäisten kulmien mittauksen mukaan. Jos sisäkulmat mittaavat alle 180 °, heptagon on kupera, mutta jos yksi tai useampi mainittu kulma ylittää 180 °, niin se on kovera.

Heptagonia, jonka sivut ovat kaikki samoja mittauksia Balaterinen. Tämä voi olla kovera tai kupera, säännöllinen tai epäsäännöllinen.

Säännöllinen ja epäsäännöllinen heptagon

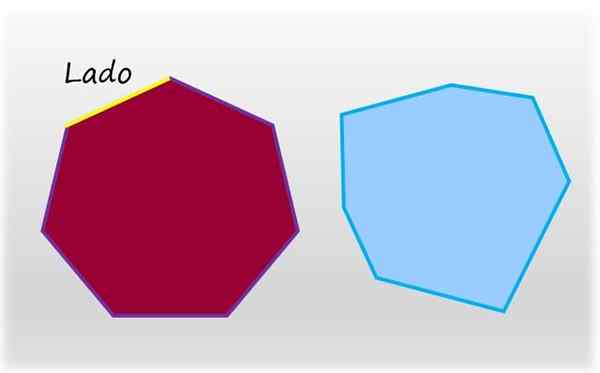Heptagon on seitsemän sivun litteä ja suljettu kuva. Vasemmalla, tavallinen heptagon, jonka sivuilla ja sisäkulmilla on yhtä suuri mitta. Oikealla puolella on epäsäännöllinen heptagon. Lähde: f. Zapata.

Tavallinen heptagon on se, jolla on seitsemän puolta ja seitsemän sisäistä kulmaa, jotka ovat yhtä suuret, vastakohta epäsäännölliselle heptagonille, jolla on ainakin yksi eri mitta tai erilainen sisäkulma.

Tavallinen heptagon

Symmetria

Tavallinen heptagon on erittäin symmetrinen hahmo. Voidaan piirtää segmenttejä, jotka yhdistävät kärkipisteen vastakkaisen puolen keskipisteeseen, jotka kaikki leikkaavat heptagonin keskellä. Nämä ovat kuviossa seitsemän symmetria -akselia.

Voi palvella sinua: tavallisen ja epäsäännöllisen Pentagonin alue: miten se otetaan, harjoitukset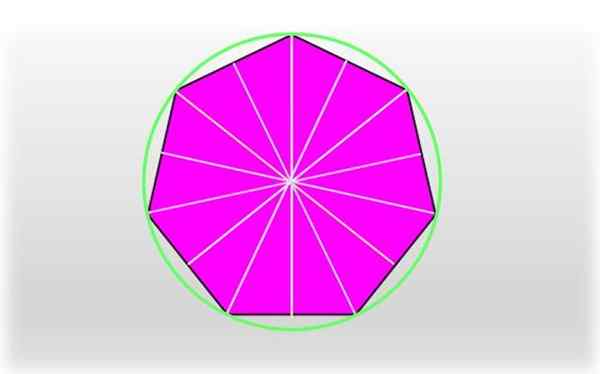 Tavallinen heptagon ja sen symmetria -akselit. Kuvan kunkin heptagonin kärkipistettä kulkevaa kehää kutsutaan ympärysmittaksi.

Segmenttiä, joka liittyy kärkipisteeseen heptagonin keskustaan, kutsutaan Kierto, Se vastaa ainutlaatuisen kehän sädettä, joka kulkee jokaisen kärjen läpi, kuten kuvassa on esitetty.

Kulmat

Heptagonissa seuraavat kulmat erottuvat:

• Sisäkulma ϕ, joiden kärkipiste on samanaikainen yhden heptagonin kärjen kanssa, joka on kulman sivut, heptagonin vierekkäiset sivut. Tavalliselle heptagonille kunkin seitsemän sisäkulman mitta on noin 128.57 °.
• Ulkokulma, Se, joka muodostuu yhden sivun ja yhden viereisen sivun pidentymisen välillä, on yleinen kärki näiden kahden puolen välillä kulman kärkipiste. Samoin muodostuu seitsemän ulkoista kulmaa ja niiden arvo lasketaan vähentämällä 180 ° sisäkulmasta, joka tavalliselle heptagonille johtaa 51.43 °.
• Keskikulma θ, Sen kärki on tavallisen heptgonin keskellä. Se lasketaan jakamalla 360 ° 7, mikä johtaa noin 51.43 °.

Sisäkulman ja keskikulman summa on yhtä suuri kuin 180 °, eli:

ϕ + θ = π

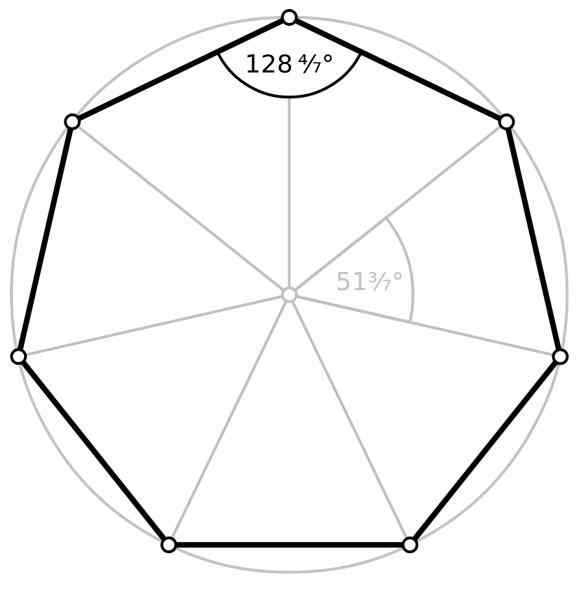Tavallisen heptagonin sisäkulma ja keskikulma. Lähde: Wikimedia Commons

Alue

Tavalliselle heptagonille on kaavoja, kun taas epäsäännöllisessä heptagonissa sinun on turvauduttava muihin menetelmiin, kuten jakamalla se muihin yksinkertaisempiin monikulmioihin, kuten kolmioihin.

Se voi palvella sinua: sääntö t: Ominaisuudet, niin että se on esimerkkejä

Säännöllinen Heptagon -alue

1. Jos kehä p ja apoteem_p-

Olipa se heptagonin alueelle. Alueen laskemiseksi on kaava, joka on voimassa jokaiselle tavalliselle monikulmiolle:

2. Jos L ja Apotem tunnetaan -lla_p-

Koska kehä on sivujen summa ja sivumitta L: n tavanomaisessa heptagonissa, se saadaan:

P = 7⋅l

Edellisen kaavan korvaaminen:

3. Jos sivu tunnetaan        

Seuraava on likimääräinen, kelvollinen kaava, kun heptagonin mitta on:

A = 3.634 ∙ L²

Epäsäännöllinen heptagonin alue

Epäsäännöllinen heptagon -alue voidaan laskea triangulaatio, joka koostuu heptagonin jakamisesta viiteen kolmioon (katso seuraava kuva). Kunkin pinta -ala on laskettu ja tulokset lisätään, mikä saa heptagonin täydellisen pinta -alan.

Toista menetelmää kutsutaan Gauss -determinantti, Ja heptagon on tarpeen sijoittaa suorakulmaiseen koordinaattijärjestelmään kunkin kärjen koordinaattien tuntemiseksi. Alue lasketaan kaavalla, joka sisältää näiden koordinaattien arvot.

Diagonaalit

Se diagonaalit Ne ovat segmenttejä, jotka yhdistävät kärkipisteen toiseen, joka ei ole peräkkäinen (jos segmentti yhdistää kaksi peräkkäistä kärkeä sivu--A. Heptagonissa on yhteensä 14 diagonaalia.

Minkä tahansa monikulmion diagonaalien D lukumäärä lasketaan kaavan kautta:

D = n · (n - 3) / 2

Korvaa n = 7, pysyy:

D = 7 · (7 - 3) / 2 = 7 · (4/2) = 14

Sisäkulmien summa

Jokaiselle heptagonille riippumatta siitä, onko se säännöllinen vai ei, sen sisäkulmien summa on yhtä suuri kuin 900 ° tai 5π radiaanit.

Se voi palvella sinua: trigonometriset syyt: esimerkkejä, harjoituksia ja sovelluksia

Tämä ominaisuus on erittäin helppo osoittaa, sillä tämä heptagon on jaettu yksittäisiin kolmioihin, jotka eivät ole päällekkäisiä, piirtäen suorasuojaussegmenttejä, jotka yhdistävät kärkipisteet, ylittämättä toisiaan.

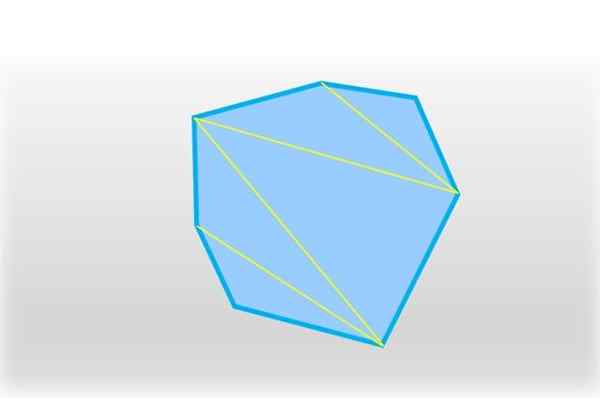Heptagon voidaan jakaa viiteen kolmioon, liittymällä segmentin kahdella ei -säilytyskipulla. Lähde: f. Zapata.

Saadaan viisi kolmiota, ja jokaisessa sen sisäkulmien summa on 180 °, joka kerrottuna 5: llä on yhtä suuri kuin 900 °:

5 x 180 ° = 900 °

Kaavat

Kehä

L -tavalliselle heptagonille kehä P lasketaan seuraavasti:

P = 7⋅l

Jos kehä on epäsäännöllinen, lisätään kunkin seitsemän sivun pituudet.

Sisäkulmamitta

Tavallisessa heptagonissa sisäkulma θ mittaa:

θ = [180 (n-2)]/n

Missä n = 7.

Apoteemi

Olla tavallisen heptagonin sivu. Apotemi on segmentti, joka menee heptagonin keskustasta, kohtisuorassa vastakkaiselle puolelle.

Antaa a_p Apoteemin pituus. Tietäen rajoitetun kehän säteen, joka on merkitty r_c Ja heptagonin L -puoli, sinulla on:

Sisäkulman θ tunteminen, yllä oleva vastaa:

Alue

Jos se on säännöllinen heptagon l: stä, alueelle A annetaan:

A = 3.634 ∙ L²

Kun heptagon on epäsäännöllinen, tarvitaan kunkin kärjen suorakulmaiset koordinaatit (x_n , ja_n), Missä n = 1, 2, 3 ... 7.

Sitten seuraavaa kaavaa käytetään alueen A löytämiseen:

Diagonaalit

Diagonaalien lukumäärä D on annettu:

D = n · (n - 3) / 2

Missä n = 7 heptagonille.

Kuinka tehdä heptagon

Seuraava animaatio osoittaa, kuinka piirtää suunnilleen tavallinen heptagon käyttämällä sääntöä ja kompassia.

Tavallisen heptagonin rakentaminen. Lähde: Wikimedia Commons

Viitteet

1. Alexander, D. 2013. Geometria. Viides. Painos. Cengage -oppiminen.
2. Lemonis, m. Tavallinen hepalle -laskin. Toipunut: Calcresource.com.
3. Matematiikan avoin viite. Monikulmioalue. Toipunut: MathPenref.com.
4. Maailmankaikkeuden kaavat. Heptagoni. Toipunut: UniversOformulat.com.
5. Wikipedia. Heptagoni. Palautettu: on.Wikipedia.com.